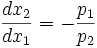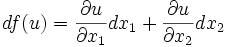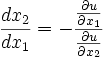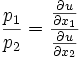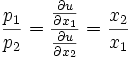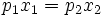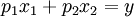- Konsummöglichkeitenkurve
-
Als Haushaltsoptimum (auch Haushaltsgleichgewicht oder Konsumoptimum) bezeichnet man in der mikroökonomischen Haushaltstheorie diejenige Konsumentscheidung eines Individuums, die es von allen ihm zu Verfügung stehenden am stärksten präferiert.
Der Optimierungsprozess geht dabei von folgenden Annahmen aus:
- Die Individuen besitzen Präferenzen bezüglich der möglichen Güterkombinationen, das heißt, sie können grundsätzlich entscheiden, ob sie eine Güterkombination einer anderen vorziehen oder aber indifferent sind (Instrumentalisierung über Indifferenzkurvensysteme).
- Die Individuen treffen ihre Konsumentscheidung auf Basis eines begrenzten Budgets (Instrumentalisierung über die Budgetgerade).
Mathematisch handelt es sich beim Haushaltsgleichgewicht um eine Maximierung unter Nebenbedingungen.
Inhaltsverzeichnis
Bestimmung des Haushaltsoptimums
Indifferenzkurven
Hauptartikel: Indifferenzkurve
Eine Indifferenzkurve (lat. indifferens: "sich nicht unterscheidend") ist die Menge aller Güterbündel, die vom Haushalt gleich gut bewertet werden, denen der Haushalt also indifferent gegenübersteht. Dabei geht man davon aus, dass solche Indifferenzkurven durch Befragen und/oder Beobachten des Haushaltes gewonnen werden können.
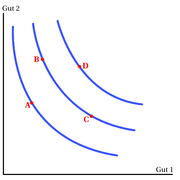
Unter gewissen Annahmen (siehe den Hauptartikel: Indifferenzkurve) existieren im zwei-dimensionalen (bzw. n-dimensionalen) reellen Güterraum unendlich viele konvexe Indifferenzkurven. Unterstellt man Nichtsättigung (mehr ist besser) so werden größere Güterbündel vorgezogen und liegen daher auf höheren Indifferenzkurven. Indifferenzkurven haben dann negative Steigung. Die Indifferenzkurve mit dem Punkt A enthält von allen eingezeichneten Kurven die am wenigsten, die Kurve mit D die am höchsten geschätzten Kombinationen. Zwischen den eingezeichneten Kurven liegen noch unendlich viele andere.
Die Steigung dx2 / dx1 der Indifferenzkurve heißt Grenzrate der Substitution. Sie gibt an, wie viel Einheiten ein Individuum bei gleichem Nutzenniveau von Gut zwei mehr benötigt, wenn es eine (marginale) Einheit von Gut eins abgibt.
Budgetgerade
Hauptartikel: Budgetgerade
Angenommen, ein Individuum verfüge über ein exogen gegebenes Einkommen und sehe sich einem bestimmten Vektor von -- als unbeeinflussbar empfundenen -- Preisen der Konsumgüter gegenüber. Die Budgetgerade (auch Konsummöglichkeitsgrenze, Budgetrestriktion, Bilanzgerade) stellt dann alle Kombinationen von Güterbündeln dar, die sich das Individuum mit seinem Einkommen gerade noch leisten kann.
Gibt es n > 1 Güter
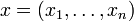 mit Preisen
mit Preisen 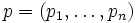 und verfügt das Individuum über ein Einkommen von y, so ist die Budgetmenge gegeben durch
und verfügt das Individuum über ein Einkommen von y, so ist die Budgetmenge gegeben durch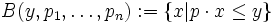 .
.
Die Budgetgerade ist jene Teilmenge von B, in welcher die schwache Ungleichung mit Gleichheit erfüllt ist, d. h., wo das Einkommen vollständig verausgabt wird. Für n = 2 ist sie in nebenstehender Zeichnung exemplarisch dargestellt. Punkt A liegt nicht auf der Budgetgeraden, sondern unterhalb, d. h. dass nicht das gesamte verfügbare Budget für die beiden zur Verfügung stehenden Güter verbraucht wird. Punkt E ist nicht erreichbar: dafür reicht das Budget nicht (der Haushalt müsste sich dafür verschulden). In Punkt B wird nichts von Gut 1 konsumiert, sondern nur Gut 2 in einer Menge von y / p2. Umgekehrt gilt dies für Punkt C. In Punkt D wird das gesamte verfügbare Einkommen ausgegeben und auf Gut 1 und Gut 2 verteilt.
In der negativen Steigung der Budgetgeraden kommt zum Ausdruck, dass bei gegebenem Einkommen ein Mehr an Konsum für Gut 1 mit einem Weniger an Konsum von Gut 2 verbunden ist. Die budgetären Opportunitätskosten entsprechen dem Preisverhältnis:
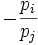
Haushaltsoptimum
Zeichnet man in das obige Indifferenzkurvensystem (mit unendlich vielen Indifferenzkurven, von denen nur einige exemplarisch gegeben sind) die Budgetgerade ein, so erkennt man, dass das Haushaltsoptimum durch einen Tangentialpunkt gegeben ist. Im Haushaltsoptimum ist also die Steigung der Indifferenzkurve gleich der Steigung der Budgetgerade:
Im Optimum ist die Grenzrate der Substitution
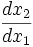 gleich dem negativen Preisverhältnis
gleich dem negativen Preisverhältnis 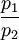
Haushaltsoptimum und Nutzenfunktion
Ordinale Nutzenfunktion
Man beachte, dass für die Bestimmung des Haushaltsoptimums und seiner wichtigsten Eigenschaft nicht das Konzept eines (messbaren, kardinalen) Nutzens benötigt wurde. Darauf hat zuerst Vilfredo Pareto aufmerksam gemacht. Häufig will man aber die Präferenzen bzw. die Indifferenzkurven durch mathematische Funktionen beschreiben. Dazu wird in folgender Weise ein ordinaler Nutzen eingeführt:
Jedem Punkt x im Indifferenzkurvensystem wird ein Nutzenindex u(x) zugeordnet, der folgende Bedingungen erfüllt, sonst aber beliebig ist:
1. Zwei Punkte, zwischen denen das Individuum indifferent ist, die also auf der gleichen Indifferenzkurve liegen, erhalten den gleichen Nutzenindex; jede Indifferenzkurve ist damit durch einen festen Wert gekennzeichnet.
2. Wird eine Kombination einer anderen vorgezogen, so erhält sie einen höheren Nutzenindex.
Die so definierte Nutzenfunktion ist monoton (wegen der Nichtsättigung) und quasikonkav (wegen der Konvexität der Indifferenzkurven) aber nicht unbedingt konkav. Sie ist nicht eindeutig, da eine monotone Transformationen einer möglichen Nutzenfunktion das gleiche Indifferenzkurvensysten beschreibt.
Die erste Ableitung der Nutzenfunktion nach der Menge eines der Konsumgüter
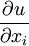 wird als Grenznutzen dieses Gutes bezeichnet.
wird als Grenznutzen dieses Gutes bezeichnet.
Es gilt für u(x) die Beziehung (siehe Totales Differential)Daraus ergibt sich für eine Indifferenzkurve (df(u) = 0):
Die Grenzrate der Substitution von Gut 2 zu Gut 1 ist gleich dem negativen Verhältnis der Grenznutzen von Gut 1 zu Gut 2. Da die Grenzrate der Substitution im Haushalsoptimum gleich dem negativen Preisverhältnis ist, ergibt sich im Haushaltsoptimum
Diese Beziehung stellt das Zweite Gossensche Gesetz dar. Man beachte, dass diese Beziehung sich bei monotoner Transformation von u(x) nicht ändert, und somit nicht vom jeweils gewählten Repräsentanten der ordinalen Nutzenfunktion abhängt.
Beispiel
Ein Haushalt möchte bei einem Einkommen von y=10 Euro und bei den Preisen von p1 = 1 und p2 = 1 sein Haushaltsoptimum bestimmen. Die Nutzenfunktion sei gegeben durch die Cobb-Douglas-Funktion
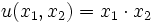 Dann gilt:
Dann gilt:und somit
Eingesetzt in die Budgetbedingung erhält man:
und somit als Nachfrage nach Gut 1 im Haushaltsoptimum:
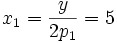 und entsprechend für Gut 2:
und entsprechend für Gut 2: 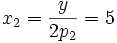
Man beachte, dass eine monotone Transformation der Nutzenfunktion (z.B.
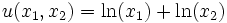 ) bei gegebenen Preisen und Einkommen zum gleichen Haushaltsoptimum führt.
) bei gegebenen Preisen und Einkommen zum gleichen Haushaltsoptimum führt.Bestimmung des Haushaltsoptimums mit Hilfe der Lagrangefunktion
Die mikroökonomische Haushaltstheorie geht davon aus, dass Individuen ihren Nutzen maximieren, wobei ihre Konsummöglichkeiten durch die Höhe des (in diesem Zusammenhang als fix vorgegeben unterstellten) Einkommens begrenzt sind.
Formal lässt sich dies wie folgt darstellen:
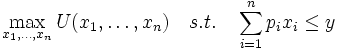
U = Nutzenfunktion, xi = Konsummenge des Gutes i, pi = Preis des Konsumgutes i, n = Anzahl der Konsumgüter, Y = Einkommen, s.t. = subject to (= unter der Nebenbedingung, dass) Dieses Maximierungsproblem unter Nebenbedingungen lässt sich mit folgendem Lagrange-Ansatz lösen:
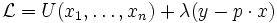
Die (unter den getroffenen Annahmen notwendigen und hinreichenden) Bedingungen erster Ordnung für eine optimale Konsumallokation lauten:
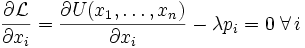
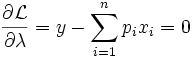
Die letzte Bedingung stellt fest, dass das gesamte Budget tatsächlich verausgabt wird. Die übrigen Bedingungen stellen fest, dass der mit ihrem Preis gewichtete Grenznutzen einer jeden Konsummenge für alle Güter gleich sein muss (nämlich dem Lagrange-Multiplikator). Der Lagrangemultiplikator misst den Wert (Schattenpreis), den das Individuum einer Erhöhung des Einkommens y (allgemein: einer marginalen Lockerung der Budgetrestriktion) beimisst. Damit erfordert ein optimaler Konsumplan, dass, sollte tatsächlich eine marginal kleine Erhöhung des Einkommens stattfinden, es dem Individuum egal ist, für welches der Güter es dieses Mehr an Einkommen ausgeben würde.
Für je zwei Güter i,j fordern die Optimalitätsbedingungen, dass die Grenzrate der Substitution gleich dem Preisverhältnis ist:
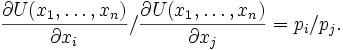
Dies ist eine sehr intuitive Bedingung: Die Grenzrate der Substitution auf der linken Seite gibt an, wie viel das Individuum maximal von Gut i aufzugeben bereit wäre, wenn es dafür eine Einheit mehr von Gut j bekommen würde (individuelle Wertschätzung). Das Preisverhältnis auf der rechten Seite gibt an, wie viel das Individuum bei gegebenen Preisen objektiv von Gut i aufgeben muss, wenn es eine Einheit mehr von Gut j erwerben würde. Bei einem optimierten Konsumplan stimmen individuelle Wertschätzung und Preisverhältnis überein.
Literatur
Varian, H. R.: Grundzüge der Mikroökonomik. 6. Aufl., München 2004, S. 19-93. Mankiw:Grundzüge der Volkswirtschaftslehre. 2. Auflage
Wikimedia Foundation.