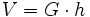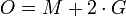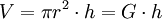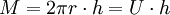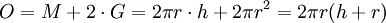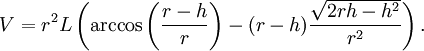Kreiszylinder

Kreiszylinder

Prismen sind auch Zylinder im allgemeinen Sinne.

gerader Zylinder mit elliptischer Grundfläche

irgendein gerader allgemeiner Zylinder

schiefer allgemeiner Zylinder

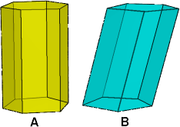
Ein Zylinder (von griech.: kylíndein = rollen, wälzen) ist laut der allgemeinen Definition von zwei parallelen, ebenen Flächen (Grund- und Deckfläche) und einer Mantel- bzw. Zylinderfläche, die von parallelen Geraden gebildet wird, begrenzt. Das heißt, er entsteht durch Verschiebung einer ebenen Fläche oder Kurve entlang einer Geraden, die nicht in dieser Ebene liegt. Sind die Geraden senkrecht zu Grund- und Deckfläche, spricht man von einem geraden Zylinder. Die Höhe des Zylinders ist gegeben durch den Abstand der beiden Ebenen, in denen Grund- und Deckfläche liegen.

Wenn in der Geometrie von einem Zylinder die Rede ist, handelt es sich jedoch häufig um einen (geraden) Kreiszylinder, wie er weiter unten beschrieben wird.

Eigenschaften

Volumen, Mantelfläche und Oberfläche berechnen sich wie folgt:

Volumen: $V = G \cdot h$

Mantelfläche: 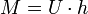$M = U \cdot h$ (nur für gerade Zylinder)

Oberfläche: $O = M + 2\cdot G$

G steht für den Inhalt der Grundfläche, U für den Umfang der Grundfläche bzw. die Länge der Leitkurve; h bezeichnet die Höhe des Zylinders.

Kreiszylinder

Ein Kreiszylinder entsteht durch Verschiebung eines Kreises parallel zu einer Geraden durch den Kreismittelpunkt, der Achse, die nicht in der Ebene des Kreises liegt. Ein Kreiszylinder wird begrenzt von zwei parallelen Kreisflächen (Grundfläche und Deckfläche) und der so genannten Mantelfläche.

Varianten

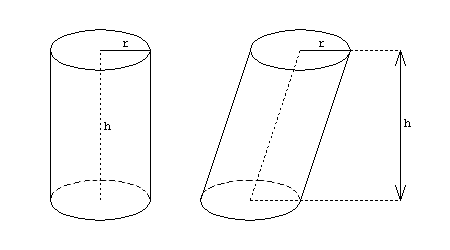
Man unterscheidet zwischen dem geraden Kreiszylinder, dessen Achse senkrecht zur Kreisebene liegt, und dem schiefen Kreiszylinder, bei dem das nicht der Fall ist. Dessen Querschnitt senkrecht zur Achse hat die Form einer Ellipse.

Besitzt der Kreiszylinder eine Bohrung entlang seiner Achse, so spricht man von einem Hohlzylinder.

Eigenschaften

Gerader Kreiszylinder mit abgewickeltem Mantel

Das Volumen eines (geraden oder schiefen) Kreiszylinders berechnet sich aus dem Grundflächenradius r und der Höhe h:

$V = \pi r^{2} \cdot h = G \cdot h$

Die Mantelfläche eines geraden Kreiszylinders berechnet sich aus:

$M = 2 \pi r \cdot h = U \cdot h$

Für die Oberfläche eines geraden Kreiszylinders ergibt sich:

$O = M + 2\cdot G = 2 \pi r \cdot h + 2 \pi r^{2} = 2 \pi r (h + r)$

Der Summand 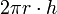$2\pi r \cdot h$ der Mantelfläche in dieser Formel ergibt sich daraus, dass diese zu einem Rechteck mit den Seitenlängen 2πr (Kreisumfang) und h (Höhe) abwickelbar ist.

Volumenberechnung eines liegenden Kreiszylinders (Tank-Problem)

Die Berechnung der Füllmenge V eines liegenden Zylinders kann anhand der Länge L, des Radius r sowie der vorliegenden Füllhöhe h vorgenommen werden. Nach der obengenannten Gleichung Volumen = Grundfläche · Höhe ergibt sich die Füllmenge durch Multiplikation des Flächeninhalts des Kreissegments mit der Länge L des Zylinders:

$V = r^2 L \left(\arccos\left(\frac{r - h}{r}\right) - (r - h) \frac{\sqrt{2rh - h^2}}{r^2}\right).$

Weblinks