Kroneckerfunktion

Das Kronecker-Delta ist ein mathematisches Zeichen, das durch ein kleines Delta mit zwei Indizes (typischerweise 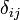$\delta_{ij}\,$) dargestellt wird und nach Leopold Kronecker benannt ist. Es wird manchmal auch als Kronecker-Symbol bezeichnet, obwohl es noch ein anderes Kronecker-Symbol gibt.

Der auch gebräuchliche Begriff Deltafunktion ist irreführend, weil damit häufiger das Dirac-Delta bezeichnet wird.

Es wird vor allem in Summenformeln im Zusammenhang mit Matrix- oder Vektoroperationen verwendet, oder um Fallunterscheidungen in Formeln zu vermeiden.

Definition

Das Kronecker-Delta ist definiert als:

$\delta_{ij} = \left\{\begin{matrix} 1 & \mbox{falls } i=j \\ 0 & \mbox{falls } i \neq j \end{matrix}\right.$.

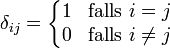Dabei können i und j Elemente einer beliebigen Menge I sein, meist jedoch einer endliche Teilmenge der natürlichen Zahlen.

Eigenschaften

Das Kronecker-Delta kann in der Form

$\delta=\mathrm{1}_D\colon I\times I\to \{0,1\}$,

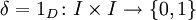geschrieben werden, ist also die charakteristische Funktion 1_D der Diagonalmenge $D=\{(i,j)\in I\times I:\; i=j\}$. Häufig wird dabei an Stelle von {0,1} ein erweiterter Bildraum, z.B. die reellen Zahlen, betrachtet.

Beispiele

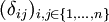• In der linearen Algebra kann die $n\times n$-Einheitsmatrix als $(\delta_{ij})_{i,j\in\{1,\ldots,n\}}$ geschrieben werden.

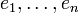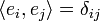• Mit dem Kronecker-Delta kann man das Skalarprodukt orthonormierter Vektoren $e_1, \dots, e_n$ als $\langle e_i, e_j\rangle = \delta_{ij}$ schreiben.

Siehe auch

• Levi-Civita-Symbol

Weblinks

• Eric W. Weisstein: Kronecker Delta auf MathWorld (englisch)