- Kruskal-Algorithmus
-
Der Algorithmus von Kruskal ist ein Algorithmus der Graphentheorie zur Berechnung minimaler Spannbäume von ungerichteten Graphen. Der Graph muss dazu zusätzlich zusammenhängend, kantengewichtet und endlich sein.
Der Algorithmus stammt von Joseph Kruskal, der ihn 1956 in der Zeitschrift „Proceedings of the American Mathematical Society“ veröffentlichte. Er beschrieb ihn dort wie folgt:
- Führe den folgenden Schritt so oft wie möglich aus: Wähle unter den noch nicht ausgewählten Kanten von G (dem Graphen) die kürzeste Kante, die mit den schon gewählten Kanten keinen Kreis bildet.[1]
Die kürzeste Kante bezeichnet dabei jeweils die Kante mit dem kleinsten Kantengewicht. Nach Abschluss des Algorithmus bilden die ausgewählten Kanten einen minimalen Spannbaum des Graphen.
Wendet man den Algorithmus auf unzusammenhängende Graphen an, so berechnet er einen minimalen Wald, also minimal spannende Bäume für jede Zusammenhangskomponente des Graphen.
Inhaltsverzeichnis
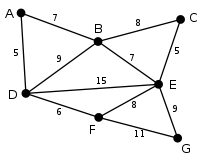
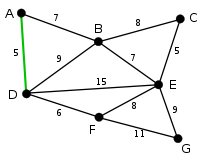
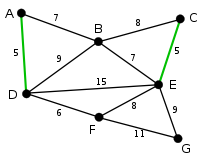
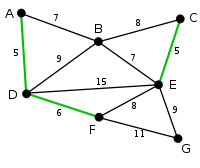
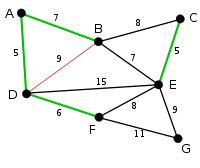
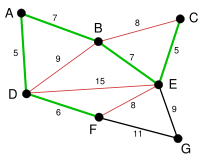
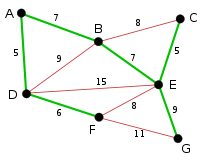
Beispiel
Formalisierter Algorithmus
Die Grundidee ist, die Kanten in Reihenfolge aufsteigender Kantengewichte zu durchlaufen und jede Kante zur Lösung hinzuzufügen, die mit allen zuvor gewählten Kanten keinen Kreis bildet. Es werden somit sukzessiv sogenannte Komponenten zum minimalen Spannbaum verbunden.
Input
Als Eingabe dient ein zusammenhängender kantenbewerteter Graph
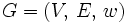 . V bezeichnet die Menge der Ecken (vertices), E die Menge der Kanten (edges). Die Gewichtsfunktion
. V bezeichnet die Menge der Ecken (vertices), E die Menge der Kanten (edges). Die Gewichtsfunktion 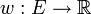 ordnet jeder Kante ein Kantengewicht zu.
ordnet jeder Kante ein Kantengewicht zu.Output
Der Algorithmus liefert einen minimalen Spannbaum
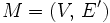 mit
mit 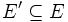 .
.Algorithmus
Der Algorithmus von Kruskal arbeitet nicht-deterministisch, d.h. er liefert unter Umständen beim wiederholten Ausführen unterschiedliche Ergebnisse. Alle diese Ergebnisse sind minimale Spannbäume von G.
G = (V,E,w): ein zusammenhängender, ungerichteter, kantengewichteter Graph
kruskal(G) 1
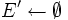 2
2 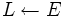 3 Sortiere die Kanten in L aufsteigend nach ihrem Kantengewicht.
4 solange
3 Sortiere die Kanten in L aufsteigend nach ihrem Kantengewicht.
4 solange 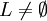 5 wähle eine Kante
5 wähle eine Kante 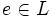 mit kleinstem Kantengewicht
6 entferne die Kante e aus L
7 wenn der Graph
mit kleinstem Kantengewicht
6 entferne die Kante e aus L
7 wenn der Graph 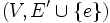 keinen Kreis enthält
8 dann
keinen Kreis enthält
8 dann 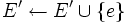 9 M = (V,E') ist ein minimaler Spannbaum von G.
9 M = (V,E') ist ein minimaler Spannbaum von G.
Derselbe Algorithmus lässt sich analog für einen maximalen Spannbaum anwenden. Sei G = (V,E,w) etwa ein zusammenhängender kantengewichteter Graph. Dann gibt man G' = (V,E,w') mit w'(e) = s − w(e),
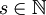 und
und 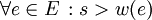 im Algorithmus von Kruskal ein. Als Ausgabe erhält man schließlich einen minimalen Spannbaum von G' und somit einen maximalen von G.
im Algorithmus von Kruskal ein. Als Ausgabe erhält man schließlich einen minimalen Spannbaum von G' und somit einen maximalen von G.Korrektheitsbeweis
Sei G = (V,E,w) ein zusammenhängender kantengewichteter Graph und M = (V,E') die Ausgabe des Algorithmus von Kruskal. Um nun die Korrektheit des Algorithmus zu beweisen, muss Folgendes gezeigt werden:
- der Algorithmus terminiert (er enthält keine Endlosschleife).
- M ist ein minimaler Spannbaum von G, also:
- M ist spannender Teilgraph von G.
- M enthält keinen Kreis.
- M ist zusammenhängend.
- M ist bezüglich G minimal.
Im Nachstehenden folgen einige Beweisideen, die die Gültigkeit der einzelnen Aussagen darlegen:
- Terminierung
- Durch Zeile 6 wird in jedem Schleifendurchlauf genau ein Element aus L entfernt. Außerdem wird L durch keine weitere Operation verändert. Aus L werden wegen Zeile 4 nur solange Elemente entfernt, bis
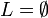 . Da zu Beginn im Algorithmus L = E gesetzt wurde und E nach Definition nur endlich ist, wird auch die Schleife nur endlich oft durchlaufen. Daraus kann man folgern, dass Kruskals Algorithmus terminiert.
. Da zu Beginn im Algorithmus L = E gesetzt wurde und E nach Definition nur endlich ist, wird auch die Schleife nur endlich oft durchlaufen. Daraus kann man folgern, dass Kruskals Algorithmus terminiert. - M ist spannender Teilgraph von G
- Da die Menge der Knoten nach Definition des Algorithmus bei M und G gleich ist und wegen Zeile 8 offensichtlich
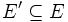 gilt, ist M spannender Teilgraph von G.
gilt, ist M spannender Teilgraph von G. - M enthält keinen Kreis
- Dass M keinen Kreis beinhalten kann, ist durch Zeile 7 trivial.
- M ist zusammenhängend
- Im Folgenden wird indirekt gezeigt, dass M zusammenhängend ist. Sei M also nicht zusammenhängend. Dann gibt es in M zwei Knoten x und y, die nicht durch einen Weg verbunden sind. Da aber x und y in G durch einen Weg verbunden sind, existiert eine Kante k in G, welche nicht in M vorhanden ist. Der Algorithmus betrachtet in Zeile 7 garantiert jede Kante aus G und damit auch k. Der Graph
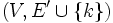 in Zeile 7 muss kreisfrei sein, da es zwischen x und y in M = (V,E') keinen Weg gibt. Mit Zeile 8 wird k dann in M eingefügt. Dies widerspricht allerdings der Tatsache, dass k nicht in M enthalten ist. Somit ist unsere Annahme hinfällig und M doch zusammenhängend.
in Zeile 7 muss kreisfrei sein, da es zwischen x und y in M = (V,E') keinen Weg gibt. Mit Zeile 8 wird k dann in M eingefügt. Dies widerspricht allerdings der Tatsache, dass k nicht in M enthalten ist. Somit ist unsere Annahme hinfällig und M doch zusammenhängend. - M ist bezüglich G minimal
- Dies ergibt sich aus dem allgemeineren Satz, dass jeder Greedy-Algorithmus (wie der Kruskal-Algorithmus einer ist) auf einem Matroid (wie das System der Bäume in einem zusammenhängenden Graph eines ist) eine Lösung minimalen Gewichts findet. In diesem Spezialfall lautet der Beweis[2]:
- Bei nur einer Kante kann nichts schiefgehen, die kleinste Kantenzahl, bei der der Algorithmus scheitern kann, muss also größer als 1 sein. Angenommen, bei dieser kleinsten Kantenzahl erzeuge der Algorithmus den Baum M, aber M' sei ein Spannbaum geringeren Gewichts als M. Beide Spannbäume enthalten gleich viele Kanten. Sortiert man alle Kanten so, dass leichtere vor schwereren liegen, dann gibt es einen minimalen Index i, für den die i-te Kante aus M schwerer ist als die i-te Kante aus M'. Man betrachtet den Teilbaum
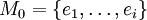 , den der Algorithmus nach Hinzunahme der ersten i Kanten erzeugt hat. Dann gibt es unter den ersten i Kanten aus M' eine, gegen die ei ausgetauscht werden kann, so dass sich ein neuer Baum
, den der Algorithmus nach Hinzunahme der ersten i Kanten erzeugt hat. Dann gibt es unter den ersten i Kanten aus M' eine, gegen die ei ausgetauscht werden kann, so dass sich ein neuer Baum 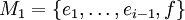 ergibt. f ist entweder die i-te Kante aus M' und damit leichter als ei, oder f ist die j-te Kante aus M' (mit j < i) und damit wegen der Minimalität von i nicht schwerer als ej, also wiederum leichter als ei. M1 ist also leichter als M0. Weil der Algorithmus bei kleinerer Kantenzahl aber funktioniert, muss M0 = M und i = | M | sein, und ei = | E | ist als letzte Kante aus M schwerer als die letzte Kante aus M'. Somit besteht der Spannbaum M' nur aus einer Teilmenge der ersten | E | − 1 Kanten und ist auch für den darauf eingeschränkten Graph G' ein Spannbaum, während der Algorithmus, angewendet auf G', den Baum
ergibt. f ist entweder die i-te Kante aus M' und damit leichter als ei, oder f ist die j-te Kante aus M' (mit j < i) und damit wegen der Minimalität von i nicht schwerer als ej, also wiederum leichter als ei. M1 ist also leichter als M0. Weil der Algorithmus bei kleinerer Kantenzahl aber funktioniert, muss M0 = M und i = | M | sein, und ei = | E | ist als letzte Kante aus M schwerer als die letzte Kante aus M'. Somit besteht der Spannbaum M' nur aus einer Teilmenge der ersten | E | − 1 Kanten und ist auch für den darauf eingeschränkten Graph G' ein Spannbaum, während der Algorithmus, angewendet auf G', den Baum 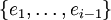 konstruiert. Weil der Algorithmus bei dieser kleineren Kantenzahl funktioniert, ist dies ein Spannbaum für G' mit i − 1 Kanten, andererseits hat G' den Spannbaum M' mit einer Kante mehr, was nicht sein kann.
konstruiert. Weil der Algorithmus bei dieser kleineren Kantenzahl funktioniert, ist dies ein Spannbaum für G' mit i − 1 Kanten, andererseits hat G' den Spannbaum M' mit einer Kante mehr, was nicht sein kann.
Zeitkomplexität
Im folgenden sei
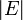 die Anzahl der Kanten und
die Anzahl der Kanten und 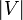 die Anzahl der Knoten. Die Laufzeit des Algorithmus setzt sich zusammen aus dem notwendigen Sortieren der Kanten nach ihrem Gewicht und dem Überprüfen, ob der Graph kreisfrei ist. Das Sortieren benötigt eine Laufzeit von
die Anzahl der Knoten. Die Laufzeit des Algorithmus setzt sich zusammen aus dem notwendigen Sortieren der Kanten nach ihrem Gewicht und dem Überprüfen, ob der Graph kreisfrei ist. Das Sortieren benötigt eine Laufzeit von 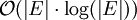 , was der Größenordnung
, was der Größenordnung 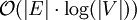 entspricht, da der Graph zusammenhängend ist und somit
entspricht, da der Graph zusammenhängend ist und somit 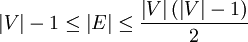 gilt. Bei einer geeigneten Implementierung ist das Überprüfen auf Kreisfreiheit schneller möglich, so dass das Sortieren die Gesamtlaufzeit bestimmt. Insbesondere bei Graphen mit vielen Kanten ist insofern der Algorithmus von Prim effizienter.
gilt. Bei einer geeigneten Implementierung ist das Überprüfen auf Kreisfreiheit schneller möglich, so dass das Sortieren die Gesamtlaufzeit bestimmt. Insbesondere bei Graphen mit vielen Kanten ist insofern der Algorithmus von Prim effizienter.Wenn die Kanten bereits vorsortiert sind, arbeitet der Algorithmus von Kruskal schneller. Man betrachtet nun, wie schnell das Überprüfen auf Kreisfreiheit möglich ist. Um eine bestmögliche Laufzeit zu erreichen, speichert man alle Knoten in einer Union-Find-Struktur. Diese enthält Informationen darüber, welche Knoten zusammenhängen. Zu Beginn ist noch keine Kante in den Spannbaum eingetragen, daher ist jeder Knoten für sich in einer einzelnen Partition. Wenn eine Kante (v1,v2) hinzugefügt werden soll, wird überprüft, ob v1 und v2 in verschiedenen Partitionen liegen. Dazu dient die Operation Find(x): Sie liefert einen Repräsentant der Partition, in dem der Knoten x liegt. Wenn Find(v1) und Find(v2) verschiedene Ergebnisse liefern, dann kann die Kante hinzugefügt werden und die Partitionen der beiden Knoten werden vereinigt (Union). Ansonsten würde durch Hinzunehmen der Kante ein Kreis entstehen, die Kante wird also verworfen. Insgesamt wird die Operation Find
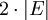 (für jede Kante) und die Operation Union
(für jede Kante) und die Operation Union 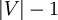 mal aufgerufen. Bei Verwenden der Heuristiken Union-By-Size und Pfadkompression ergibt eine amortisierte Laufzeitanalyse für den Algorithmus [3] eine Komplexität von
mal aufgerufen. Bei Verwenden der Heuristiken Union-By-Size und Pfadkompression ergibt eine amortisierte Laufzeitanalyse für den Algorithmus [3] eine Komplexität von 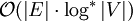 . Dabei ist log * definiert als
. Dabei ist log * definiert als 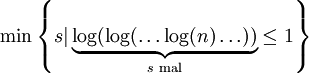 und praktisch konstant.
und praktisch konstant.Sonstiges
Der Algorithmus diente Kruskal ursprünglich als Hilfsmittel für einen vereinfachten Beweis, dass ein Graph mit paarweise verschiedenen Kantengewichten einen eindeutigen minimalen Spannbaum besitzt.
Weblinks
- Vollständiger Beweis zur Korrektheit des Algorithmus von Kruskal, Ronny Harbich, 2006
- Anschauliche Darstellung des Algorithmus im Rahmen des Informatik Jahres 2006
- Interaktives Java-Applet zur Demonstration
- Weiteres Java-Applet
Quellen und Bemerkungen
- ↑ Joseph Kruskal: On the shortest spanning subtree and the traveling salesman problem. In: Proceedings of the American Mathematical Society. 7 (1956), S. 48–50
- ↑ Hubertus Th. Jongen: Optimierung B. Skript zur Vorlesung, Aachen: Verlag der Augustinus-Buchhandlung, ISBN 3-925038-19-1
- ↑ Skript Theoretische Informatik III
Wikimedia Foundation.