Pfadkompression

Eine Union-Find-Datenstruktur verwaltet die Partition einer Menge. Der abstrakte Datentyp wird durch die Menge der drei Operationen {Union, Find, Make-Set} gebildet. Union-Find-Strukturen dienen zur Verwaltung von Zerlegungen in disjunkten Mengen. Dabei bekommt jede Menge der Zerlegung ein kanonisches Element zugeordnet, dieses dient als Name der Menge. Union vereinigt zwei solche Mengen, Find(x) bestimmt das kanonische Element derjenigen Menge, die x enthält und Make- Set erzeugt eine Einermenge {x} mit dem kanonischen Element x.

Anwendungen

Union-Find-Strukturen eignen sich gut, um Zusammenhangskomponenten von Graphen zu verwalten. Der Algorithmus von Kruskal z.B. erfordert eine solche Datenstruktur, um effizient implementiert werden zu können.

Definition

Eine endliche Menge S sei in die disjunkten Klassen X_i partitioniert:

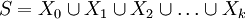$S = X_0 \cup X_1 \cup X_2 \cup \ldots \cup X_k$ mit $X_i \cap X_j = \varnothing \quad\forall i, j \in \lbrace 0, 1, \ldots, k \rbrace, i \neq j$.

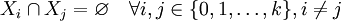Zu jeder Klasse X_i wird ein Repräsentant 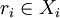$r_i \in X_i$ ausgewählt. Die zugehörige Union-Find-Struktur unterstützt die folgenden Operationen effizient:

• Init(S): Initialisiert die Struktur und bildet für jedes 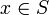$x \in S$ eine eigene Klasse mit x als Repräsentant.
• Union(r, s): Vereinigt die beiden Klassen, die zu den beiden Repräsentanten r und s gehören, und bestimmt r zum neuen Repräsentanten der neuen Klasse.
• Find(x): Bestimmt zu 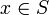$x \in S$ den eindeutigen Repräsentanten, zu dessen Klasse x gehört.

Implementierung

Eine triviale Implementierung speichert die Zugehörigkeiten zwischen den Elementen aus S und den Repräsentanten r_i in einem Array. Für kürzere Laufzeiten werden jedoch in der Praxis Mengen von Bäumen verwendet. Dabei werden die Repräsentanten in den Wurzeln der Bäume gespeichert, die anderen Elemente der jeweiligen Klasse in den Knoten darunter.

• Union(r, s): Hängt die Wurzel des niedrigeren Baumes als neues Kind unter die Wurzel des höheren Baumes (gewichtete Vereinigung). Falls nun r Kind von s ist, werden r und s vertauscht.
• Find(x): Wandert vom Knoten x aus den Pfad innerhalb des Baumes nach oben bis zur Wurzel und gibt diese als Ergebnis zurück.

Heuristiken

Um die Operationen Find und Union zu beschleunigen, gibt es die zwei Heuristiken Union-By-Size und Pfadkompression.

Union-By-Size

Bei der Operation Union(r,s) wird der Baum, der kleiner ist, unter den größeren Baum gehängt. Damit verhindert man, dass einzelne Teilbäume zu Listen entarten können wie bei der naiven Implementation (r wird in jedem Fall Wurzel des neuen Teilbaums). Die Tiefe eines Teilbaums T kann damit nicht größer als 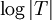$\log \left|T\right|$ werden. Mit dieser Heuristik verringert sich die Worst-Case-Laufzeit von Find von O(n) auf O(logn). Für eine effiziente Implementation führt man bei jeder Wurzel die Anzahl der Elemente im Teilbaum mit.

Pfadkompression

Um spätere Find(x) Suchvorgänge zu beschleunigen, versucht man die Wege vom besuchten Knoten zur zugehörigen Wurzel zu verkürzen.

maximale Verkürzung (Wegkompression)

Nach dem Ausführen von Find(x) werden alle Knoten auf dem Pfad von x zur Wurzel direkt unter die Wurzel gesetzt. Dieses Verfahren bringt im Vergleich zu den beiden folgenden den größten Kostenvorteil für nachfolgende Aufrufe von Find für einen Knoten im gleichen Teilbaum. Zwar muss dabei jeder Knoten auf dem Pfad zwischen Wurzel und x zweimal betrachtet werden, für die Laufzeit ist das jedoch egal.

Aufteilungsmethode (splitting)

Während des Durchlaufes lässt man jeden Knoten auf seinen bisherigen Großvater zeigen (falls vorhanden); damit wird ein durchlaufender Pfad in zwei der halben Länge zerlegt.

Halbierungsmethode (halving)

Während des Durchlaufes lässt man jeden zweiten Knoten auf seinen bisherigen Großvater zeigen.

Diese Methoden haben beide dieselben amortisierten Kosten wie die oberste Kompressionsmethode (Knoten unter die Wurzel schreiben). Alle Kompressionsmethoden beschleunigen zukünftige Find(x)-Operationen.

Laufzeiten

Union-Find-Datenstrukturen ermöglichen die Ausführung der obigen Operationen mit den folgenden Zeitkomplexitäten ($n=\left| S \right|$):

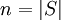Triviale Implementierung mit einem Array A (A[i] = x: Knoten i liegt in der Menge x), worst-case: Find O(n), Union: O(1)

Implementierung mit Bäumen:

• ohne Heuristiken: Find O(n), Union O(1)
• mit Union-By-Size, worst-case: Find O(log(n)), Union O(1)
• mit Union-By-Size, Pfadkompression, worst-case: Find O(log(n)), Union O(1)
• mit Union-By-Size, Pfadkompression, Folge von f Find- und u Union-Operationen (amortisiert): $O\left(u + (n + f)\cdot(\log^*(n))\right)$

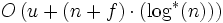
Weblinks

• http://www.cs.unm.edu/~rlpm/499/uf.html Java-Applet zur Demonstration von Union-Find
• http://research.cs.vt.edu/algoviz/UF Noch ein Java-Applet zu Union-Find