Lagarias

Jeffrey Clark Lagarias (* 16. November 1949 in Pittsburgh) ist ein US-amerikanischer Mathematiker und Informatiker.

Lagarias war 1970 Putnam Fellow (als Sieger des Wettbewerbs) und studierte am MIT, wo er 1974 bei Harold Stark promoviert wurde. Ab 1975 war er an den ATT Bell Labs, wo er Distinguished Member of the Technical Staff wurde. Seit 1995 ist er Berater (Technology Consultant) bei ATT Research Laboratories. 2002 wurde er Professor an der University of Michigan.

Lagarias arbeitete unter anderem über Zahlentheorie, Komplexitätstheorie, Kryptographie, mathematische Physik, dynamische Systeme, niedrig dimensionale Topologie (Knotentheorie) und diskrete Geometrie (wie Kreispackungen, Quasikristalle). Er fand mit Peter Shor 1992 ein Gegenbeispiel zur Keller-Vermutung. Außerdem bewies er, dass folgende elementare Vermutung äquivalent zur Riemannschen Vermutung ist:

Für alle n > 0 gilt 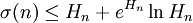    $\sigma(n) \le H_n + e^{H_n} \ln{H_n}$     und das Gleichheitszeichen darin nur für n = 1.

Dabei ist σ(n) die Summe der Teiler von n und 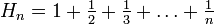$H_n = 1 + \tfrac{1}{2} + \tfrac{1}{3} + \ldots + \tfrac{1}{n}$ die n-te harmonische Zahl.

Er arbeitete auch über das Collatz-Problem.

Schriften

• The 3x+1 problem and its generalizations, American Mathematical Monthly 92, 1985, S. 3–23
• An elementary problem equivalent to the Riemann hypothesis, American Mathematical Monthly 109, 2002, S. 534–543.

Weblinks

• Homepage von Lagarias an der Universität Michigan

Personendaten
NAME	Lagarias, Jeffrey
KURZBESCHREIBUNG	US-amerikanischer Mathematiker
GEBURTSDATUM	16. November 1949
GEBURTSORT	Pittsburgh