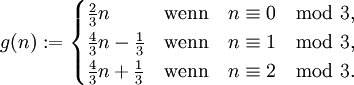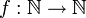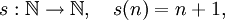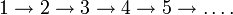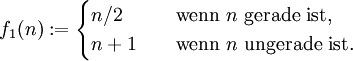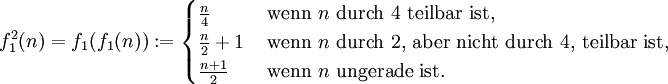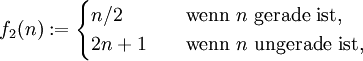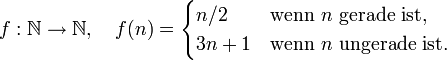3n+1

Das Collatz-Problem, auch als (3n + 1)-Vermutung bezeichnet, ist ein ungelöstes mathematisches Problem, das 1937 von Lothar Collatz entdeckt wurde.

Problemstellung

Bei dem Problem geht es um Zahlenfolgen, die nach einem einfachen Bildungsgesetz konstruiert werden:

• Beginne mit irgendeiner natürlichen Zahl n.
• Ist n gerade, so nimm als nächstes n / 2,
• ist n ungerade, so nimm als nächstes 3n + 1.

So erhält man z. B. für die Startzahl n = 19 die Folge

19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1

Erstaunlicherweise endete die Folge bisher immer mit …, 4, 2, 1 – egal welche Startzahl man probiert hat. Die Collatz-Vermutung lautet:

Jede so konstruierte Zahlenfolge endet im Zykel 4,2,1 egal, mit welcher natürlichen Zahl man beginnt.

Trotz zahlreicher Anstrengungen gehört diese Vermutung noch immer zu den ungelösten Problemen der Mathematik. Mehrfach wurden Preise für eine Lösung ausgelobt:

• 1970 bot H. S. M. Coxeter 50 $ für einen Beweis der Vermutung und 100 $ für ein Gegenbeispiel.
• Bryan Thwaites hat 1996 1000 englische Pfund versprochen.
• Paul Erdős bot 500 Pfund für eine Lösung, sagte aber über das Collatz-Problem:

  „Mathematics is not yet ready for such problems.“ (Die Mathematik ist noch nicht bereit für solche Probleme.)

Ursprung und Geschichte

Der Ursprung der Collatz-Vermutung liegt insofern etwas im Nebel, als aus der mutmaßlichen Entstehungszeit bisher keine schriftlichen Dokumente mit einer Beschreibung des Problems öffentlich zugänglich sind.

Publizierte Quellen

• 1974: Ein Informatik-Lehrbuch^[1] enthält die erste schriftliche Publikation des Collatz-Problems.
• 1976: Riho Terras ist der Autor der ersten wissenschaftlichen Publikation mit Forschungsergebnissen zum Collatz-Problem.^[2]
• 1985: In der Zeitschrift American Mathematical Monthly erscheint ein Überblicksartikel von Jeffrey C. Lagarias^[3]. Lagarias berichtet darin über Collatz’ Interesse an zahlentheoretischen Funktionen und Graphentheorie, und er zitiert einen Notizbucheintrag vom 1. Juli 1932, in dem Collatz die folgende ganzzahlige Funktion betrachtet:

$g(n) := \begin{cases} \tfrac23 n &\mbox{wenn}\quad n\equiv 0 \mod3, \\ \tfrac43 n-\tfrac13 &\mbox{wenn}\quad n\equiv1\mod3, \\ \tfrac43n+\tfrac13 &\mbox{wenn}\quad n\equiv2\mod3.\end{cases}$

Diese Funktion besitzt den Fixpunkt 1 und unter Iteration die Zykel (2,3) und (4,5,7,9,6). In dem zitierten Notizbucheintrag stellt Collatz die auch heute noch offene Frage, ob die mit 8 beginnende g-Trajektorie zyklisch wird oder gegen Unendlich divergiert.

• 1985: Bryan Thwaites^[4] publiziert die Behauptung, er habe es am 21. Juli 1952 um vier Uhr nachmittags gefunden.
• 1986: Lothar Collatz lässt eine Darstellung seines Entdeckungswegs zur (3n+1)-Vermutung ins Chinesische übersetzen und im Journal einer Universität in China veröffentlichen.^[5]

Der Collatz-Graph einer Funktion

Collatz’ Beschreibung seiner Motivation der (3n+1)-Vermutung ist sehr plausibel^[6]: Er assoziiert zunächst ganz allgemein zu einer beliebigen Funktion auf den natürlichen Zahlen mit Werten in den natürlichen Zahlen einen gerichteten Graphen, der von Lagarias im oben erwähnten Überblicksartikel Collatz-Graph genannt wird. Der Collatz-Graph einer zahlentheoretischen Funktion

$f:\mathbb{N}\to \mathbb{N}$

ist ein gerichteter Graph, bestehend aus der Menge der natürlichen Zahlen als Knotenmenge und zu jeder natürlichen Zahl n einer gerichteten Kante von n nach f(n).

Die einfachste solche Funktion ist die Nachfolgerabbildung

$s:\mathbb{N}\to\mathbb{N},\quad s(n)= n+1,$

deren Collatz-Graph aus einem unendlich langen Weg besteht:

$1\to 2\to 3\to 4\to 5\to \ldots.$

Um mehr Beispiele zu haben, suchte er zunächst nach einer möglichst „einfachen“ zahlentheoretischen Funktion, deren Collatz-Graph einen Kreis enthält. Eine solche Funktion f muss auf gewissen natürlichen Zahlen n „aufsteigen“, also die Relation n < f(n) erfüllen, und auf anderen natürlichen Zahlen m „absteigen“, also die Relation m > f(m) erfüllen. So stieß er zunächst auf die Funktion

$f_1(n) := \begin{cases}n/2 &amp;amp;\mbox{wenn } n\mbox{ gerade ist,}\\ n+1\quad&amp;amp;\mbox{wenn } n\mbox{ ungerade ist.}\end{cases}$

Den Collatz-Graph dieser Funktion kann man wie folgt beschreiben: Jeder Knoten k ist, nach Definition, eine natürliche Zahl. Falls k>1, besitzt k die beiden Vorgängerknoten k-1 und 2k, und der Knoten k=1 besitzt nur den Knoten 2 als Vorgänger. Außerdem gilt

$f_1^2(n) = f_1(f_1(n)) := \begin{cases}\frac{n}{4} &amp;amp;\mbox{wenn } n\mbox{ durch 4 teilbar ist,}\\ \frac{n}2+1 &amp;amp;\mbox{wenn }n\mbox{ durch 2, aber nicht durch 4, teilbar ist,}\\ \frac{n+1}2\quad&amp;amp;\mbox{wenn } n\mbox{ ungerade ist.}\end{cases}$

Daraus folgt

$f_1^2(n)&amp;lt;n\qquad\mbox{ wenn }n&amp;gt;2,$

und das hat zur Folge, dass der Collatz-Graph von f₁ nur den Kreis (1,2) besitzt, und dass die f₁-Trajektorie zu jeder beliebigen Startzahl in diesen Kreis mündet.

Weil diese Argumentation ziemlich einfach ist, suchte Collatz weiter: der Collatz-Graph der Funktion

$f_2(n) := \begin{cases}n/2 &amp;amp;\mbox{wenn } n\mbox{ gerade ist,}\\ 2n+1\quad&amp;amp;\mbox{wenn } n\mbox{ ungerade ist,}\end{cases}$

enthält keinen Kreis, da jede ungerade Zahl auf eine größere ungerade Zahl abgebildet wird, und die f₂-Trajektorien daher alle gegen Unendlich divergieren.

Der nächste Versuch ist die Collatz-Funktion

$f:\mathbb{N}\to\mathbb{N}, \quad f(n) = \begin{cases} n/2 &amp;amp;\mbox{wenn } n \mbox{ gerade ist,} \\ 3n +1 &amp;amp; \mbox{wenn } n \mbox{ ungerade ist.} \end{cases}$

Zu dieser Funktion fand Collatz nur den „trivialen Kreis“ (1,4,2) – er schreibt, er habe seine Ideen deshalb nicht veröffentlicht, weil er nicht beweisen konnte, dass der „triviale Kreis“ der einzige sei.

Verbreitung des Collatz-Problems

Als Lothar Collatz 1952 seine Professur in Hamburg antrat, erzählte er seinem Hamburger Kollegen Helmut Hasse von diesem Problem. Dieser verbreitete das Problem während eines Forschungsaufenthalts an der Syracuse University, deshalb erhielt das Collatz-Problem auch den Namen Syracuse-Algorithmus. Stanisław Marcin Ulam (Los Alamos) und Shizuo Kakutani (Yale) haben das Problem immer wieder in Gesprächen gestellt und werden deshalb in diesem Zusammenhang häufig genannt.

Nach Terras’ Publikation 1976 begann nach und nach eine rege wissenschaftliche Beschäftigung mit dem Collatz-Problem, die mittlerweile weit mehr als hundert Publikationen mit neuen Forschungsergebnissen umfasst. Im populärwissenschaftlichen Bereich entstanden neue Bezeichnungen:

• Douglas R. Hofstadter^[7] nannte in seinem Buch Gödel, Escher, Bach diejenigen Startzahlen, deren Collatz-Trajektorie im Zykel (1,4,2) endet, wondrous numbers (wundersame Zahlen).
• Nach Clifford A. Pickover^[8] werden sie auch hailstone numbers (Hagelschlag-Zahlen) genannt.

Prinzipielles

Prinzipiell kann eine f-Trajektorie als Zahlenfolge eine der drei folgenden Eigenschaften haben:

• die Folge endet im 1-Zyklus.
• die Folge wächst über alle Grenzen.
• die Folge gerät in einen anderen Zyklus.

Computer haben alle Zahlen bis 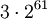$3\cdot 2^{61}$ (Stand 2008) durchprobiert; immer endet die Zahlenfolge mit 1, bestätigt also die Vermutung.

Falls eine Folge in einen anderen Zyklus geraten könnte, müsste dieser aus mindestens 275.000 Zahlen bestehen, wie J. C. Lagarias 1985 zeigte.^[3]

Lösungsansätze

Man hat mit unterschiedlichen Methoden versucht, das Problem zu lösen. Eine davon ist die systematische Suche nach Gegenbeispielen mit Computerunterstützung.

Collatz-Problem in den ganzen Zahlen

Für das von den natürlichen Zahlen (positive) auf die ganzen Zahlen (Null und negative) ausgeweitete Collatz-Problem, wurden außer dem 1-4-2-1-Zyklus noch vier weitere Zyklen gefunden:

• 0, 0
• -1, -2, -1
• -5, -14, -7, -20, -10, -5 und
• -17, -50, -25, -74, -37, -110, -55, -164, -82, -41, -122, -61, -182, -91, -272, -136, -68, -34, -17.

Verallgemeinerungen des Problems

Audrey Terras gewinnt Teilerkenntnisse über Zyklen, indem sie als Anfangswert auch negative Zahlen zulässt (1976, 1979). Marc Chamberland definierte eine stetige Funktion, welche die diskrete Collatz-Folge auf den Bereich der reellen Zahlen erweitert. Simon Letherman, Dierk Schleicher und Reg Wood betrachten Funktionen im Bereich der komplexen Zahlen als Erweiterung. Allgemeine Vermutung: (3n + 3^x) endet immer in 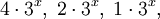$4\cdot 3^x,\; 2\cdot 3^x,\; 1\cdot3^x,$ und besitzt nur diesen einen Zyklus.

Graphentheorie

Man untersucht den so genannten Collatz-Baum oder Collatz-Graphen. Dies ist ein Baum, dessen Knotenmenge die Menge der natürlichen Zahlen ist; der Knoten 1 ist die Wurzel des Baums. Jeder Knoten hat einen oder zwei Vorgänger, nämlich die Zahlen, von denen aus durch Anwendung der Iterationsvorschrift der Knoten erreicht wird. 1 hat den Vorgänger 2 (denn 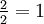$\tfrac22 = 1$), 16 hat die Vorgänger 32 und 5 (denn 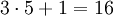$3\cdot 5+1 = 16$). Jede Zahl n hat den Vorgänger 2n, und nur die Zahlen n kongruent 4 modulo 6 haben noch einen zweiten Vorgänger, nämlich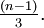 $\tfrac{(n-1)}3.$

Mit diesem Graphen beschäftigen sich unter anderem Paul J. Andaloro, Stefan Andrei, Manfred Kudlek und Raud Stefan Niculescu. Sie gewinnen unendliche Teilmengen der natürlichen Zahlen, für welche die Collatz-Folge bei 1 endet.

Literatur

• Günther J. Wirsching: The Dynamical System Generated by the 3n+1 Function, Springer- Verlag, Berlin 1998, ISBN 3-540-63970-5.

Weblinks

• On The 3x+1 Problem and its generalizations Ein Übersichtsartikel zum Collatz-Problem von Jeff Lagarias (englisch)
• On The 3x+1 Problem, ein Distributed-computing-Projekt, das sich mit dem Collatz-Problem beschäftigt (englisch)
• Collatz Rechner

Einzelnachweise

1. ↑ Jürg Nievergelt, J.C.Farrar und E.M.Reingold: Computer Approaches to Mathematical Problems, Prentice Hall, Inc., Enlgewood Cliffs, New Jersey, 1974, ISBN 978-0131648555.
2. ↑ Riho Terras: A stopping time problem on the positive integers, Acta Arith. XXX (1976), 141-152.
3. ↑ ^{a b} Jeff Lagarias: On The 3x+1 Problem and its generalizations. American Mathematical Monthly Volume 92, 1985, S. 3–23. [1]
4. ↑ Bryan Thwaites: My conjecture, Bull., Inst. Math. Appl. 21 (1985), 35-41.
5. ↑ Lothar Collatz: About the motivation of the (3n+1)-problem, J. Qufu Norm. Univ., Nat. Sci. 3 (1986), 9-11. (Chinesisch)
6. ↑ siehe Günther J. Wirsching: Über das (3n+1)-Problem, Elem. Math. 55 (2000), 142-155.
7. ↑ Douglas R. Hofstadter: Gödel, Escher, Bach, Penguin Books, Harmondsworth 1980, 400-402
8. ↑ Clifford A. Pickover: Hailstone (3n+1) Number Graphs, J. Recreational Math. 21 (1989), 120-123