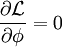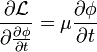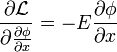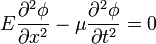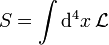- Lagrangedichte
-
Betrachtet man in der theoretischen Physik das Verhalten von Feldern, so geht die Lagrange-Funktion L über in ein Integral über die Lagrange-Dichte
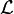 , welche die Dichte der Lagrange-Funktion in einem Volumenelement beschreibt.
, welche die Dichte der Lagrange-Funktion in einem Volumenelement beschreibt.Sie ist definiert als
mit dem betrachteten Feld Φ(x,y,z,t).
Der eigentliche Zweck der Lagrange-Dichte ist die Beschreibung von Feldern durch Bewegungsgleichungen. So, wie man die Lagrange-Gleichungen 2. Art aus dem Hamiltonschen Prinzip erhält, kann man die Lagrange-Gleichungen für Felder aus dem Hamiltonschen Prinzip für Felder erhalten (Herleitung). Entsprechend lautet die Bewegungsgleichung
Beispiel
Für eine in einer Dimension schwingende Saite ergibt sich für die Lagrange-Dichte
In diesem Beispiel bedeuten:
- φ = φ(x,t) die Auslenkung eines Punktes der Saite aus der Ruhelage (Feldvariable)
- μ die lineare Massendichte
- E den Elastizitätsmodul
Mit dieser Lagrange-Dichte ergibt sich
Damit ergibt sich für die Bewegungsgleichung der schwingenden Saite
Anwendung in der Relativitätstheorie
Anwendung findet die Beschreibung physikalischer Vorgänge über die Lagrange-Dichte statt über die Lagrange-Funktion vor allem in relativistischen Vorgängen. Hier ist eine kovariante Darstellung der Lagrange-Funktion gewünscht, dann ist die Wirkung über
definiert. Dann ist die Lagrange-Funktion ein Lorentz-Skalar, also invariant unter Lorentz-Transformationen:
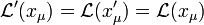 mit x'μ = Λμνxν, wobei Λμν der Lorentz-Transformationstensor ist.
mit x'μ = Λμνxν, wobei Λμν der Lorentz-Transformationstensor ist.
Wikimedia Foundation.

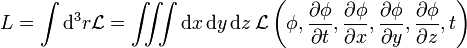
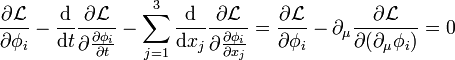
![\mathcal{L} = \frac{1}{2} \left[\mu \left(\frac{\partial \phi}{\partial t}\right)^2 - E \left(\frac{\partial \phi}{\partial x} \right)^2 \right]](/pictures/dewiki/99/c229de3ff501ec74a1478ca5a879881c.png)