- Klein-Gordon
-
Mit ihrer Klein-Gordon-Gleichung versuchten Oskar Klein und Walter Gordon Wellenfunktionen zu charakterisieren, die in der Quantenmechanik den Zuständen eines freien, relativistischen Teilchens entsprechen. Zwar ergibt sich aus ihr die richtige Beziehung zwischen Energie und Impuls, nicht aber der Spin des Teilchens. Bei geladenen Spin-1/2-Teilchen, wie dem Elektron und dem Proton im Wasserstoffatom, stimmen die Bindungsenergien, die man aus der Klein-Gordon-Gleichung herleitet, nicht mit den beobachteten Energien überein, weil sie nicht die Spins beider Teilchen berücksichtigt.
Die Klein-Gordon-Gleichung beschreibt spinlose Teilchen, beispielsweise Pionen, die in der Kernphysik ein Yukawa-Potential zwischen den Protonen und Neutronen im Kern bewirken.
Inhaltsverzeichnis
Herleitung
Bei der Herleitung geht man von der Energie-Impuls-Beziehung
zwischen der Energie E und dem Impuls
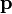 eines Teilchens der Masse m in der Speziellen Relativitätstheorie aus.
eines Teilchens der Masse m in der Speziellen Relativitätstheorie aus.Die Erste Quantisierung deutet diese Gleichung als Gleichung für Operatoren, die auf Wellenfunktionen
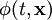 wirken. Dabei sind E und
wirken. Dabei sind E und 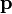 die Operatoren
die OperatorenDamit ergibt sich für Wellenfunktionen
 die den quantenmechanischen Zuständen des relativistischen Teilchens der Masse m entsprechen, die Klein-Gordon-Gleichung
die den quantenmechanischen Zuständen des relativistischen Teilchens der Masse m entsprechen, die Klein-Gordon-GleichungAn Stelle der SI-Einheiten verwendet man in der relativistischen Quantentheorie natürliche Einheiten, in denen
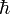 und c den Wert 1 haben. In diesen Einheiten und mit dem Wellenoperator
und c den Wert 1 haben. In diesen Einheiten und mit dem Wellenoperatorund mit der abkürzenden Bezeichnung
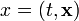 für die Raumzeitkoordinaten ist die Klein-Gordon-Gleichung einfach
für die Raumzeitkoordinaten ist die Klein-Gordon-Gleichung einfachLagrangedichte
Die Lagrangedichte für ein reelles Feld
 , die auf die Klein-Gordon-Gleichung führt, lautet
, die auf die Klein-Gordon-Gleichung führt, lautetBei einem komplexen Feld φ wählt man die Normierung
Hierbei ist
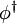 das komplex konjugierte Feld. Mit dieser Normierung ergeben sich in der Quantenfeldtheorie für das komplexe Feld dieselben Propagatoren wie für das reelle.
das komplex konjugierte Feld. Mit dieser Normierung ergeben sich in der Quantenfeldtheorie für das komplexe Feld dieselben Propagatoren wie für das reelle.Kontinuitätsgleichung
Die Lagrangedichte für das komplexe Feld ist invariant unter der kontinuierlichen Schar von Transformationen
die das Feld mit einer komplexen Phase
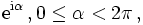 multiplizieren. Nach dem Noether-Theorem gehört zu dieser kontinuierlichen Symmetrie ein erhaltener Strom mit Komponenten
multiplizieren. Nach dem Noether-Theorem gehört zu dieser kontinuierlichen Symmetrie ein erhaltener Strom mit KomponentenDie 0-Komponente ist die Dichte der erhaltenen Ladung,
Diese Dichte ist nicht positiv definit und kann nicht als Wahrscheinlichkeitsdichte gedeutet werden. Vielmehr ist
die elektrische Ladung und jm die elektromagnetische Viererstromdichte, an die das skalare Potential und das Vektorpotential der Elektrodynamik koppeln.
Lösung der Klein-Gordon-Gleichung
Die ebene Welle
ist eine Lösung der Klein-Gordon-Gleichung, wenn die Kreisfrequenz ω gemäß
mit dem Wellenvektor
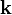 zusammenhängt. Ebenso löst die konjugiert komplexe Welle
zusammenhängt. Ebenso löst die konjugiert komplexe Welledie Klein-Gordon-Gleichung, denn sie ist reell.
Da die Klein-Gordon-Gleichung linear ist, sind Summen und komplexe Vielfache von Lösungen ebenso Lösungen. Daher löst
mit beliebigen Fouriertransformierbaren Amplituden
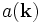 und
und 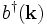 die Klein-Gordon-Gleichung. Umgekehrt ist jede Fouriertransformierbare Lösung von dieser Form.
die Klein-Gordon-Gleichung. Umgekehrt ist jede Fouriertransformierbare Lösung von dieser Form.In dieser Darstellung der Lösung ist allerdings nicht ersichtlich, dass sie im Punkt x nur von ihren Anfangswerten auf und im Inneren des Lichtkegels von x abhängt.
In der Quantenfeldtheorie (in der die angegebenen Normierungsfaktoren verwendet werden) ist φ ein Operator. Der Operator
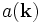 vernichtet in Teilchenzuständen spinlose Teilchen, beispielsweise negative Pionen,
vernichtet in Teilchenzuständen spinlose Teilchen, beispielsweise negative Pionen, 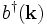 erzeugt die entgegengesetzt geladenen Antiteilchen, positive Pionen. Der adjungierte Operator
erzeugt die entgegengesetzt geladenen Antiteilchen, positive Pionen. Der adjungierte Operator 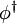 vernichtet dann positive Pionen und erzeugt negative Pionen.
vernichtet dann positive Pionen und erzeugt negative Pionen.Für ein relles Feld
 gilt
gilt 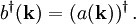 Es ist invariant unter Phasentransformationen und trägt nicht zum elektromagnetischen Strom bei. Die Teilchen, die das reelle Feld vernichtet und erzeugt, sind ungeladen und stimmen mit ihren Antiteilchen, beispielsweise neutralen Pionen, überein.
Es ist invariant unter Phasentransformationen und trägt nicht zum elektromagnetischen Strom bei. Die Teilchen, die das reelle Feld vernichtet und erzeugt, sind ungeladen und stimmen mit ihren Antiteilchen, beispielsweise neutralen Pionen, überein.Siehe auch
Literatur
- N. N. Bogoliubov, D. V. Shirkov, Introduction to the Theory of Quantized Fields, Wiley-Interscience, New York, 1959
- Richard Courant und David Hilbert, Methoden der mathematischen Physik, Band 2, Springer Verlag, zweite Auflage 1968
Wikimedia Foundation.

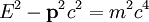
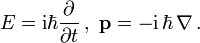
![\left[ \frac{1}{c^2} \frac{\partial^2}{\partial t^2} - \mathbf{\nabla}^2 + \frac{m^2 c^2}{\hbar^2} \right] \phi(t, \mathbf{x}) = 0\,.](/pictures/dewiki/56/8057fc415dc19f1401abe5daf1cc55b5.png)

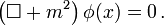
![\mathcal{L} = \frac{1}{2} \left[ (\partial_t \varphi)^2
- (\partial_x \varphi)^2 - (\partial_y \varphi)^2 - (\partial_z \varphi)^2 - m^2 \varphi^2 \right]\,.](/pictures/dewiki/99/ce669033aab9a85200908a45fe1ccb36.png)



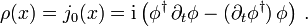
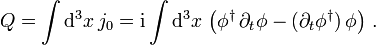

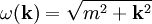

![\phi(x) = \int\!\! \frac{\mathrm{d}^3 k}{(2\pi)^3\,2\, \omega(\mathbf{k})} \left[
a(\mathbf{k})\,\mathrm e^{\mathrm i \bigl( \mathbf k\cdot \mathbf x - \omega(\mathbf k)\,t\bigr)}+
b^\dagger (\mathbf{k})\,\mathrm e^{-\mathrm i \bigl( \mathbf k\cdot \mathbf x -\omega(\mathbf k)\,t\bigr)}\right]](/pictures/dewiki/55/71501d2af2bac24837985648f2d453fb.png)