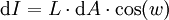Lambert-Verteilung

Das Lambertsche Gesetz (Lambertsches Kosinusgesetz), formuliert von Johann Heinrich Lambert, beschreibt die Abhängigkeit der Lichtstärke eines ideal diffus reflektierenden Flächenstücks (einer sogenannten Lambert-Fläche) vom Betrachtungswinkel θ.

Beschreibung

Unebene Oberfläche als Modellvorstellung für diffuse Streuung, die nicht notwendigerweise dem Lambertschen Gesetz gehorcht.

L sei eine Konstante, A ein Flächenelement und θ der Ausstrahlungswinkel (Betrachtungswinkel) bezogen auf die Flächennormale, dann gilt für die Lichtstärke I einer lambertschen Fläche das lambertsche Kosinusgesetz:

$I = A \cdot \cos(\theta)\cdot L$.

Das Verhältnis von Lichtstärke und reduzierter Fläche (in Betrachtungsrichtung projiziert),

$\frac{I}{A \cdot \cos(\theta)} = L$

ist gerade die Leuchtdichte der Fläche. Sie ist bei einer Lambert-Fläche von der Betrachtungsrichtung unabhängig. Papier z. B. folgt in guter Näherung dem lambertschen Gesetz: es erscheint gleich hell, egal, von welcher Richtung man darauf schaut.

Eine Lambert-Fläche reflektiert maximal senkrecht zur Oberfläche, unabhängig von der Einstrahlungsrichtung.

Die Beleuchtung einer Lambertschen Fläche hängt vom Einstrahlungswinkel w zur Normalen ab. Die Abhängigkeit ergibt sich aus der effektiven Fläche pro Flächenelement, die mit dem Kosinus von w kleiner wird (wegen der perspektivischen Verkürzung).

Für ein Flächenelement dA und einen festen Betrachtungswinkel gilt:

$\mathrm{d}I = L \cdot \mathrm{d}A \cdot \cos(w)$

Anschaulich: Die Helligkeit ist abhängig vom Winkel w zwischen dem Vektor zur Lichtquelle und dem Oberflächennormalenvektor. Ein großer Winkel w bedeutet einen flachen Lichteinfall, der einen kleineren Lichtstrom pro Flächeneinheit ergibt. Daraus resultiert dann die geringere Intensität der diffusen Reflexion.

Die Leuchtdichte resultiert aus dem Beitrag vieler Flächenelemente. Bei Betrachtung unter schrägem Blickwinkel schrumpft die Größe der Flächenelemente um cos(θ). Da die Bezugsfläche unverändert ist, nimmt die Zahl der Flächenelemente, die zur Leuchtdichte beitragen, entsprechend zu. Gleichzeitig sinkt ihre Lichtstärke aber um cos(θ). Die Leuchtdichte ist von θ unabhängig.

Beispiel

Reflexionsverhalten eines dünnen, senkrecht zur Bildebene stehenden Papierstreifens (links und rechts) und eines Transparentpapier-Streifens (3. von links)

Eine gute Näherung für einen Lambert-Strahler ist Papier. Kleine Lufteinschlüsse zwischen den Fasern bilden Streuzentren für das sichtbare Licht. Fehlen sie, zum Beispiel durch Tränken des Papiers mit Wasser, verliert Papier seine Reflexionseigenschaften und wird transparent.

Die Bilder oben veranschaulichen die Aussage des Lambertschen Gesetzes an einem Experiment. Von links strahlt rotes Licht auf einen dünnen Papierstreifen, der senkrecht zur Bildebene steht. Im linken Bild trifft die Strahlung senkrecht auf den Streifen, im mittleren Bild im Winkel von ca. 45° auf den gedrehten Streifen. Im dritten Bild bestrahlt das Licht Transparentpapier im Winkel von 45°.

Die Streueigenschaften von Papier kommen denen einer Lambert-Fläche recht nahe. Die diffuse Rückstreuung ist in der Richtung senkrecht zum Papierstreifen am größten und unabhängig von der Einstrahlungsrichtung. Dies gilt auch für durchscheinende Streuscheiben (mattes Milchglas) und ansatzweise auch für Transparentpapier.

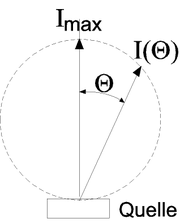
Das vierte Teilbild zeigt schematisch die kreisförmige Kosinus-Abhängigkeit der Intensität vom Ausstrahlungswinkel für eine nichttransparente Lambertsche Fläche.

Lambert-Strahler

Ein Lambert-Strahler ist ein physikalisch idealer Strahler. Die Strahldichte (bzw. Leuchtdichte) eines Lambert-Strahlers ist nach allen Richtungen konstant. Beispiel: Eine glühende Kugel erscheint in allen Richtungen gleichmäßig hell. Ein schwarzer Strahler etwa absorbiert Strahlung und emittiert sie entsprechend dem Lambertschen Gesetz. Die Helligkeit einer glühenden Metallplatte ändert sich nicht, wenn sie gegenüber der Blickrichtung verkippt wird. Als Lambert-Strahler wird also eine Strahlungsquelle bezeichnet, deren Strahlstärke einem cos-Gesetz folgt:

$I = I_{max} \cos \, \theta$

Dabei kennzeichnet θ = 0 die Hauptstrahlrichtung (siehe Bild).

Typische Lambert-Strahler sind Leuchtdioden ohne Plastiklinse und die Dipolantenne (λ/2-Dipol).

Siehe auch

• Ulbricht-Kugel