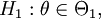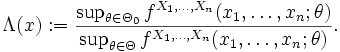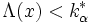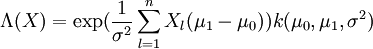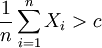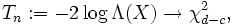- Likelihood-Ratio-Test
-
Der Likelihood-Quotienten-Test oder Likelihood-Ratio-Test ist ein statistischer Test, der zu den typischen Hypothesentests in parametrischen Modellen gehört. Viele klassische Tests wie der F-Test für den Varianzenquotienten oder der Zwei-Stichproben-t-Test lassen sich als Beispiele für Likelihood-Quotienten-Tests interpretieren.
Inhaltsverzeichnis
Definition
Formal betrachtet man das typische parametrische Testproblem: Gegeben ist eine Grundmenge von Wahrscheinlichkeitsverteilungen
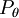 , abhängig von einem unbekannten Parameter
, abhängig von einem unbekannten Parameter 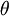 , der aus einer bekannten Grundmenge
, der aus einer bekannten Grundmenge 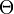 stammt. Als Nullhypothese
stammt. Als Nullhypothese 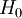 soll getestet werden, ob der Parameter zu einer echten Teilmenge
soll getestet werden, ob der Parameter zu einer echten Teilmenge 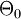 gehört. Also:
gehört. Also: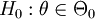 .
.
Die Alternative
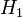 lautet entsprechend:
lautet entsprechend:wobei
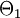 das Komplement zu
das Komplement zu 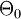 in
in 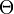 bezeichnet.
bezeichnet.Die beobachteten Daten sind Realisierungen von Zufallsvariablen
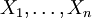 , die jeweils die (unbekannte) Verteilung
, die jeweils die (unbekannte) Verteilung 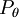 besitzen und stochastisch unabhängig sind.
besitzen und stochastisch unabhängig sind.Der Begriff des Likelihood-Quotienten-Tests suggeriert bereits, dass die Entscheidung des Tests auf der Bildung eines Quotienten beruht. Man geht dabei so vor, dass man ausgehend von den Daten
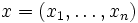 und den zu den einzelnen Parametern gehörenden Dichtefunktionen
und den zu den einzelnen Parametern gehörenden Dichtefunktionen 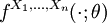 den folgenden Ausdruck berechnet:
den folgenden Ausdruck berechnet:Heuristisch gesprochen: Man bestimmt anhand der Daten zunächst den Parameter aus der gegebenen Grundmenge, der die größte Wahrscheinlichkeit dafür liefert, dass die gefundenen Daten gemäß der Verteilung
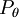 realisiert worden sind. Der Wert der Dichtefunktion bezüglich dieses Parameters wird dann als repräsentativ für die gesamte Menge gesetzt. Im Zähler betrachtet man als Grundmenge den Raum der Nullhypothese, also
realisiert worden sind. Der Wert der Dichtefunktion bezüglich dieses Parameters wird dann als repräsentativ für die gesamte Menge gesetzt. Im Zähler betrachtet man als Grundmenge den Raum der Nullhypothese, also 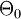 , für den Nenner betrachtet man die gesamte Grundmenge
, für den Nenner betrachtet man die gesamte Grundmenge 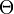 .
.Es lässt sich intuitiv schließen: Je größer der Quotient ist, desto wahrscheinlicher ist
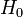 . Ein Wert von
. Ein Wert von 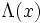 in der Nähe von Eins bedeutet, dass anhand der Daten kein großer Unterschied zwischen den beiden Parametermengen
in der Nähe von Eins bedeutet, dass anhand der Daten kein großer Unterschied zwischen den beiden Parametermengen 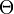 und
und 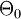 zu erkennen ist. Die Nullhypothese sollte in solchen Fällen also nicht verworfen werden.
zu erkennen ist. Die Nullhypothese sollte in solchen Fällen also nicht verworfen werden.Demnach wird bei einem Likelihood-Quotienten-Test die Hypothese
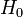 zum Niveau
zum Niveau 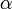 abgelehnt, falls
abgelehnt, fallsgilt. Hierbei ist der kritische Wert
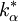 so zu wählen, dass
so zu wählen, dass 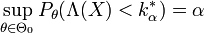 gilt.
gilt.Die konkrete Bestimmung dieses kritischen Werts ist in der Regel problematisch.
Beispiel
Für unabhängige Zufallsvariablen
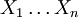 , die jeweils eine Normalverteilung mit bekannter Varianz
, die jeweils eine Normalverteilung mit bekannter Varianz 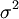 und unbekanntem Erwartungswert
und unbekanntem Erwartungswert 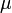 besitzen, ergibt sich für das Testproblem
besitzen, ergibt sich für das Testproblem 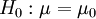 gegen
gegen 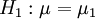 mit
mit 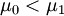 der folgende Likelihood-Quotient:
der folgende Likelihood-Quotient:mit der von den konkreten Daten unabhängigen Konstanten
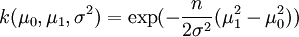 . Man erhält dann, dass
. Man erhält dann, dass 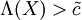 äquivalent zur Ungleichung
äquivalent zur Ungleichungist. Dies liefert als Resultat den bekannten Gauß-Test; man wählt
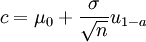 , wobei
, wobei 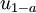 das
das 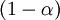 -Quantil einer Standardnormalverteilung bezeichnet.
-Quantil einer Standardnormalverteilung bezeichnet.Approximation von
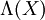 durch eine χ²-Verteilung
durch eine χ²-VerteilungUnter bestimmten Voraussetzungen lässt sich die im allgemeinen schwierig zu betrachtende Teststatistik
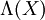 durch χ²-verteilte Zufallsvariablen annähern, so dass sich vergleichsweise leicht asymptotische Tests herleiten lassen. Neben eher technischen Annahmen an die Verteilungsfamilie
durch χ²-verteilte Zufallsvariablen annähern, so dass sich vergleichsweise leicht asymptotische Tests herleiten lassen. Neben eher technischen Annahmen an die Verteilungsfamilie 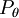 ist die folgende Annahme einer „Parametrisierbarkeit der Nullhypothese“ fundamental:
ist die folgende Annahme einer „Parametrisierbarkeit der Nullhypothese“ fundamental:Es seien der Parameterraum
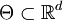 und zudem
und zudem 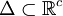 gegeben, beide Mengen seien offen und es gelte:
gegeben, beide Mengen seien offen und es gelte: 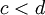 . Zudem existiere eine zweimal stetig differenzierbare Abbildung
. Zudem existiere eine zweimal stetig differenzierbare Abbildung 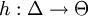 mit
mit 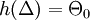 , deren Jacobi-Matrix
, deren Jacobi-Matrix 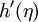 für jedes
für jedes 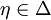 vollen Rang besitzt.
vollen Rang besitzt.Dann gilt:
wobei die Zufallsvariablen in Verteilung konvergieren.
Die Beweisidee beruht auf einer Aussage über die Existenz von Maximum-Likelihood-Schätzern in allgemeinen parametrischen Familien und ihrer Konvergenz gegen eine normalvereilte Zufallsvariable, deren Varianz das Inverse der Fisher-Information ist.
Literatur
P. J. Bickel, K. Doksum: Mathematical statistics. Holden-Day.
Wikimedia Foundation.