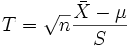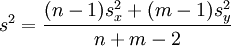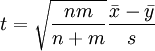- T-Test
-
Der t-Test ist ein Begriff aus der mathematischen Statistik, er bezeichnet eine Gruppe von Hypothesentests. Den t-Test im eigentlichen Sinn gibt es nicht. Es handelt sich hier lediglich um einen beliebigen Hypothesentest mit t-verteilter Testprüfgröße.
Oft ist jedoch mit dem t-Test der Einstichproben- bzw. Zweistichproben t-Test gemeint:
- Der Einstichproben t-Test prüft anhand des Mittelwertes einer Stichprobe, ob der Erwartungswert einer Grundgesamtheit ungleich, kleiner oder größer einem vorgegebenem Wert ist.
- Der Zweistichproben t-Test prüft anhand der Mittelwerte zweier Stichproben, ob die Erwartungswerte zweier Grundgesamtheiten ungleich, kleiner oder größer sind.
Weitere wichtige Tests mit t-verteilter Prüfgröße sind:
- Test der Koeffizienten einer Regressionsanalyse bei normalverteilter Störgröße,
- Test des Korrelationskoeffizienten zweier normalverteilter Zufallsvariablen.
Der t-Test ist ein Spezialfall des Wald-Tests.
Inhaltsverzeichnis
Einstichproben t-Test
Grundidee für den t-Test über den Erwartungswert einer normalverteilten Grundgesamtheit
Sind
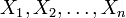 unabhängige normalverteilte Zufallsvariablen mit Erwartungswert μ und Standardabweichung σ, dann ist ihr arithmetisches Mittel
unabhängige normalverteilte Zufallsvariablen mit Erwartungswert μ und Standardabweichung σ, dann ist ihr arithmetisches Mittel 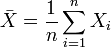 ebenfalls normalverteilt mit Erwartungswert μ und hat die Standardabweichung
ebenfalls normalverteilt mit Erwartungswert μ und hat die Standardabweichung 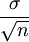 . Daher ist der standardisierte Mittelwert
. Daher ist der standardisierte Mittelwert 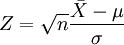 standardnormalverteilt und könnte mit einem Gauß-Test getestet werden.
standardnormalverteilt und könnte mit einem Gauß-Test getestet werden.Normalerweise ist jedoch die Standardabweichung unbekannt. In diesem Fall liegt es nahe, sie durch die empirische Standardabweichung
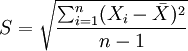 zu schätzen und als Teststatistik
zu schätzen und als Teststatistikzu verwenden. Dieser Wert ist allerdings nicht mehr normalverteilt, sondern t-verteilt mit n − 1 Freiheitsgraden. Ist er für eine konkrete Stichprobe so groß (oder so klein), dass dieser oder ein noch extremerer Wert unter der Nullhypothese hinreichend unwahrscheinlich ist, wird die Nullhypothese abgelehnt.
Grundidee für den t-Test über den Erwartungswert einer beliebig verteilten Grundgesamtheit
Sind
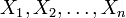 (n > 30) unabhängige beliebig verteilte Zufallsvariablen mit Erwartungswert
(n > 30) unabhängige beliebig verteilte Zufallsvariablen mit Erwartungswert 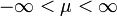 und Standardabweichung
und Standardabweichung 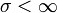 , dann ist aufgrund des zentralen Grenzwertsatzes ihr arithmetisches Mittel
, dann ist aufgrund des zentralen Grenzwertsatzes ihr arithmetisches Mittel 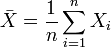 ebenfalls approximativ normalverteilt mit Erwartungswert μ und hat die Standardabweichung
ebenfalls approximativ normalverteilt mit Erwartungswert μ und hat die Standardabweichung 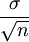 . Mit der gleichen Argumentation wie zuvor gelangt man zu einer t-verteilten Teststatistik
. Mit der gleichen Argumentation wie zuvor gelangt man zu einer t-verteilten TeststatistikVorgehen
Für eine Stichprobe
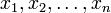 aus einer normalverteilten Grundgesamtheit mit unbekanntem Erwartungswert μ und unbekannter Standardabweichung σ soll die Nullhypothese H0:μ = μ0 (mit einem festen vermuteten Wert μ0) gegen die zweiseitige Alternative
aus einer normalverteilten Grundgesamtheit mit unbekanntem Erwartungswert μ und unbekannter Standardabweichung σ soll die Nullhypothese H0:μ = μ0 (mit einem festen vermuteten Wert μ0) gegen die zweiseitige Alternative 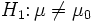 getestet werden. Dazu wird mit dem Stichprobenmittelwert
getestet werden. Dazu wird mit dem Stichprobenmittelwert 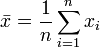 und der Stichprobenstandardabweichung
und der Stichprobenstandardabweichung 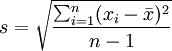 die Testprüfgröße
die Testprüfgröße 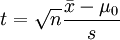 berechnet. Die Nullhypothese wird zum Signifikanzniveau α abgelehnt, falls
berechnet. Die Nullhypothese wird zum Signifikanzniveau α abgelehnt, falls 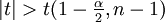 ist, dem
ist, dem 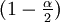 -Quantil der t-Verteilung mit n − 1 Freiheitsgraden.
-Quantil der t-Verteilung mit n − 1 Freiheitsgraden.Die Prüfgröße t kann auch zum Testen der einseitigen Alternative μ > μ0 gegen die Nullhypothese
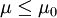 zum Signifikanzniveau α verwendet werden. Diese wird nun abgelehnt, wenn
zum Signifikanzniveau α verwendet werden. Diese wird nun abgelehnt, wenn 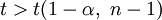 gilt. Analog wird die Nullhypothese
gilt. Analog wird die Nullhypothese 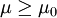 abgelehnt, wenn
abgelehnt, wenn 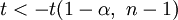 ist.
ist.Beispiel 1
Es soll getestet werden, ob die durchschnittliche Laufzeit von Notebook-Akkus tatsächlich mindestens 3,5 Stunden beträgt, wie vom Hersteller behauptet. Dazu werden bei 10 Akkus dieser Marke unter kontrollierten gleichen Bedingungen die Laufzeiten gemessen. Es ergibt sich ein empirischer Mittelwert von 3,25 Stunden mit einer Standardabweichung von 0,31 Stunden. Daraus berechnet sich als Prüfgröße ein t-Wert von
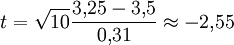 . Für das 0,95-Quantil der t-Verteilung mit 10 − 1 = 9 Freiheitsgraden findet man mit Hilfe einer t-Tabelle oder eines Computerprogramms den Wert t(0,95;9) = 1,833. Wegen t < − 1,833 kann die Nullhypothese, dass der Erwartungswert der Laufzeit größer oder gleich 3,5 Stunden ist, zum Signifikanzniveau
. Für das 0,95-Quantil der t-Verteilung mit 10 − 1 = 9 Freiheitsgraden findet man mit Hilfe einer t-Tabelle oder eines Computerprogramms den Wert t(0,95;9) = 1,833. Wegen t < − 1,833 kann die Nullhypothese, dass der Erwartungswert der Laufzeit größer oder gleich 3,5 Stunden ist, zum Signifikanzniveau 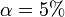 abgelehnt werden. Die Akkus erreichen also nicht die behaupteten Laufzeiten.
abgelehnt werden. Die Akkus erreichen also nicht die behaupteten Laufzeiten.Kompaktdarstellung
Einstichproben t-Test Voraussetzungen 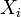 unabhängig voneinander
unabhängig voneinander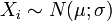 oder
oder 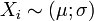 mit n > 30
mit n > 30
Hypothesen 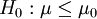
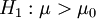
(rechtsseitig)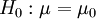
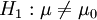
(zweiseitig)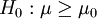
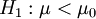
(linksseitig)Teststatistik 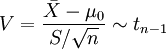
Prüfwert 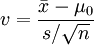 mit
mit 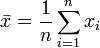 und
und 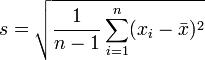
Annahmebereich H0 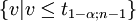
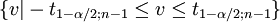
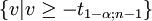
Annahmebereich H1 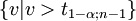
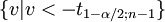
oder
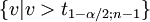
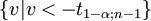
Zweistichproben t-Test
Aus der Theorie der multivariaten Normalverteilung folgt, dass die Differenz zweier normal verteilter (oder approximativ normalverteilter) Zufallsvariable wieder normalverteilt ist. Damit kann der Zweistichproben t-Test auf den Einstichproben t-Test zurückgeführt werden mit
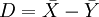 :
: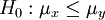
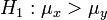
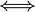
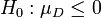
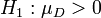
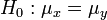
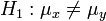
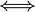
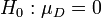
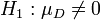
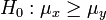
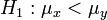
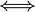
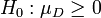
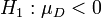
Das Problem ist die Schätzung der Varianz von
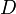 unter Gültigkeit der Nullhypothese zur Bestimmung der Verteilung der Teststatistik:
unter Gültigkeit der Nullhypothese zur Bestimmung der Verteilung der Teststatistik:- Sind die Grundgesamtheiten abhängig voneinander, dann muss der t-Test für gepaarte Stichproben durchgeführt werden.
- Sind die Grundgesamtheiten unabhängig voneinander und
- sind die Varianzen in den Grundgesamtheiten gleich, dann muss der t-Test für zwei unabhängige Stichproben durchgeführt werden und
- sind die Varianzen in den Grundgesamtheiten ungleich, dann muss der Welch-Test durchgeführt werden.
Die drei Tests unterscheiden sich im wesentlichen dadurch, wie die Varianz von
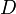 geschätzt wird. Dies beeinflusst auch die Zahl der Freiheitsgrade für die t-Verteilung der Teststatistik.
geschätzt wird. Dies beeinflusst auch die Zahl der Freiheitsgrade für die t-Verteilung der Teststatistik.t-Tests für gepaarte Stichproben
Hier sind
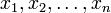 und
und 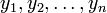 zwei paarweise verbundene Stichproben, die beispielsweise aus zwei Messungen an denselben Untersuchungseinheiten gewonnen wurden (Messwiederholung). Die Stichproben können auch aus anderen Gründen paarweise abhängig sein, z.B., wenn die x- und y-Werte Messergebnisse von Frauen bzw. Männern in einer Partnerschaft sind und Unterschiede zwischen den Geschlechtern interessieren.
zwei paarweise verbundene Stichproben, die beispielsweise aus zwei Messungen an denselben Untersuchungseinheiten gewonnen wurden (Messwiederholung). Die Stichproben können auch aus anderen Gründen paarweise abhängig sein, z.B., wenn die x- und y-Werte Messergebnisse von Frauen bzw. Männern in einer Partnerschaft sind und Unterschiede zwischen den Geschlechtern interessieren.Soll die Nullhypothese getestet werden, dass die beiden Erwartungswerte der zugrunde liegenden normalverteilten Grundgesamtheiten gleich sind, so können mit dem oben beschriebenen Einstichproben-t-Test die Differenzen di = xi − yi auf den Erwartungswert 0 getestet werden.
Beispiel 2
Um eine neue Therapie zur Senkung des Cholesterinspiegels zu testen, werden bei zehn Probanden vor und nach der Behandlung die Cholesterinwerte bestimmt. Es ergeben sich die folgenden Messergebnisse:
vor der Behandlung: 223 259 248 220 287 191 229 270 245 201 nach der Behandlung: 220 244 243 211 299 170 210 276 252 189 Differenz: 3 15 5 9 -12 21 19 -6 -7 12
Die Differenzen der Messwerte haben das arithmetisches Mittel
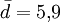 und die Stichprobenstandardabweichung sd = 11,39. Das ergibt als Prüfgrößenwert
und die Stichprobenstandardabweichung sd = 11,39. Das ergibt als Prüfgrößenwert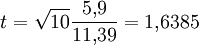 .
.
Es ist
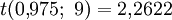 , also gilt
, also gilt 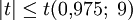 . Somit kann die Nullhypothese, dass die Erwartungswerte der Cholesterinwerte vor und nach der Behandlung gleich sind, die Therapie also keine Wirkung hat, zum Signifikanzniveau
. Somit kann die Nullhypothese, dass die Erwartungswerte der Cholesterinwerte vor und nach der Behandlung gleich sind, die Therapie also keine Wirkung hat, zum Signifikanzniveau 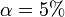 nicht abgelehnt werden. Wegen
nicht abgelehnt werden. Wegen 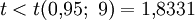 ist auch die einseitige Alternative, dass die Therapie den Cholesterinspiegel senkt, nicht signifikant. Wenn die Behandlung überhaupt einen Effekt hat, so ist dieser nicht groß genug, um ihn mit einem so kleinen Stichprobenumfang zu entdecken.
ist auch die einseitige Alternative, dass die Therapie den Cholesterinspiegel senkt, nicht signifikant. Wenn die Behandlung überhaupt einen Effekt hat, so ist dieser nicht groß genug, um ihn mit einem so kleinen Stichprobenumfang zu entdecken.Kompaktdarstellung
Zweistichproben t-Test für zwei gepaarte Stichproben Voraussetzungen 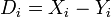 unabhängig voneinander
unabhängig voneinander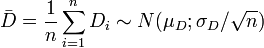 (zumindest approximativ)
(zumindest approximativ)
Hypothesen 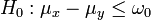
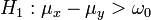
(rechtsseitig)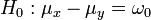
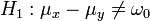
(zweiseitig)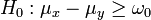
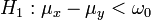
(linksseitig)Teststatistik 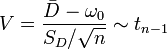
Prüfwert 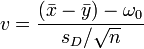 mit
mit 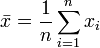 ,
, 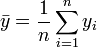
und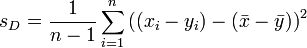
Annahmebereich H0 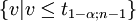
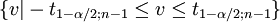
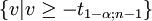
Annahmebereich H1 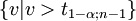
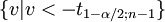
oder
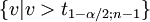
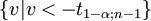
t-Tests für zwei unabhängige Stichproben
Gegeben sind nun zwei unabhängige Stichproben
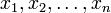 und
und 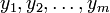 jeweils aus normalverteilten Grundgesamtheiten mit den Erwartungswerten μx bzw. μy und unbekannter, aber gleicher Standardabweichung σ. Es soll die Nullhypothese H0:μx = μy gegen die zweiseitige Alternative
jeweils aus normalverteilten Grundgesamtheiten mit den Erwartungswerten μx bzw. μy und unbekannter, aber gleicher Standardabweichung σ. Es soll die Nullhypothese H0:μx = μy gegen die zweiseitige Alternative 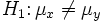 getestet werden. Dazu wird mit den Stichprobenmittelwerten
getestet werden. Dazu wird mit den Stichprobenmittelwerten 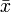 ,
, 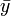 , den Stichprobenvarianzen
, den Stichprobenvarianzen 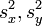 und der sogenannten gewichteten Varianz
und der sogenannten gewichteten Varianzdie Prüfgröße
berechnet. (Bei gleich großen Stichproben, also m = n, vereinfacht sich diese Formel zu
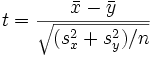 ). Die Prüfgröße ist t-verteilt mit n + m − 2 Freiheitsgraden, also wird H0 zum Signifikanzniveau α abgelehnt, wenn
). Die Prüfgröße ist t-verteilt mit n + m − 2 Freiheitsgraden, also wird H0 zum Signifikanzniveau α abgelehnt, wenn 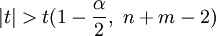 gilt. Es können auch wieder einseitige Hypothesen getestet werden: Zum Beispiel wird die Nullhypothese
gilt. Es können auch wieder einseitige Hypothesen getestet werden: Zum Beispiel wird die Nullhypothese 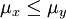 zugunsten der Alternative μx > μy abgelehnt, wenn
zugunsten der Alternative μx > μy abgelehnt, wenn 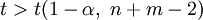 gilt.
gilt.Beispiel 3
Zwei Düngemittelsorten sollen verglichen werden. Dazu werden 10 Parzellen mit Sorte A und 15 Parzellen mit Sorte B gedüngt. Bei ersteren ergibt sich ein mittlerer Ernteertrag
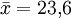 mit Stichprobenvarianz
mit Stichprobenvarianz 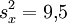 und bei den anderen Parzellen das Mittel
und bei den anderen Parzellen das Mittel 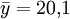 mit Varianz
mit Varianz 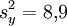 . Für die gewichtete Varianz berechnet man damit
. Für die gewichtete Varianz berechnet man damit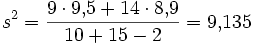 .
.
Daraus erhält man die Prüfgröße
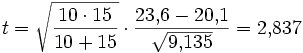 .
.
Dieser Wert ist größer als das 0,975-Quantil der t-Verteilung mit 10 + 15 − 2 = 23 Freiheitsgraden
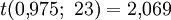 . Es kann also mit einer Konfidenz von
. Es kann also mit einer Konfidenz von 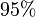 behauptet werden, dass ein Unterschied in der Wirkung der beiden Düngemittel besteht. Wegen
behauptet werden, dass ein Unterschied in der Wirkung der beiden Düngemittel besteht. Wegen 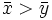 ist Sorte A besser.
ist Sorte A besser.Kompaktdarstellung
Zweistichproben t-Test für zwei unabhängige Stichproben Voraussetzungen 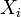 und
und 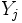 unabhängig voneinander
unabhängig voneinander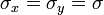 unbekannt
unbekannt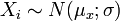 oder
oder 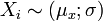 mit n > 30
mit n > 30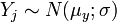 oder
oder 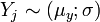 mit m > 30
mit m > 30
Hypothesen 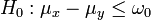
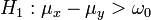
(rechtsseitig)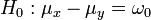
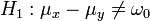
(zweiseitig)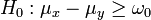
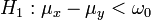
(linksseitig)Teststatistik 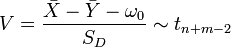
Prüfwert 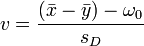 mit
mit 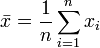 ,
,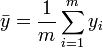 ,
, 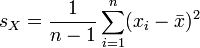 ,
,
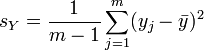 und
und 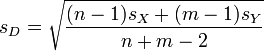
Annahmebereich H0 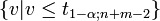
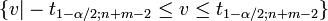
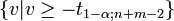
Annahmebereich H1 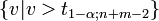
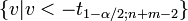
oder
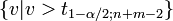
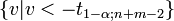
Testen der Voraussetzungen und Alternativen zum t-Test
Der t-Test wird, wie oben ausgeführt, zum Testen von Hypothesen über Erwartungswerte einer oder zweier Stichproben aus normalverteilten Grundgesamtheiten mit unbekannter Standardabweichung verwendet.
- Die Normalverteilungsannahme kann mit dem Shapiro-Wilk-Test oder dem Kolmogorow-Smirnow-Test geprüft werden. Liegt keine Normalverteilung vor, können als Ersatz für den t-Test nichtparametrische Tests angewendet werden, etwa ein Wilcoxon-Rangsummentest für unabhängige Stichproben oder ein Wilcoxon-Vorzeichen-Rang-Test für gepaarte Stichproben.
- Sollen mehr als zwei normalverteilte Stichproben auf Gleichheit der Erwartungswerte getestet werden, kann eine Varianzanalyse angewendet werden.
- Bei Mittelwertvergleichen normalverteilter Stichproben mit bekannter Standardabweichung werden Gauß-Tests verwendet.
Weblinks
Wikimedia Foundation.