- Linear temporal logic
-
Lineare temporale Logik (LTL oder Linear temporal logic) ist ein Modell temporaler Logik mit zeitlichen Modalitäten. In LTL, können Formeln über die Zukunft von Pfaden aufgestellt werden, wie dass eine Bedingung irgendwann wahr wird, eine Bedingung wahr bleibt bis eine andere Bedingung erfüllt wird, usw.
Inhaltsverzeichnis
Syntax
LTL ist aus einer Menge von Aussagenvariablen p1,p2,..., den logischen Verknüpfungen
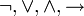 und den nachfolgenden temporalen modalen Operatoren aufgebaut:
und den nachfolgenden temporalen modalen Operatoren aufgebaut:- X für Nachfolger (N wird synonym benutzt)
- G für global
- F für irgendwann (finally)
- U für bis (until)
- R für Auflösung (release).
Die ersten drei Operatoren sind unär, so dass X φ eine syntaktisch korrekte Formel ist, wenn φ syntaktisch korrekt ist. Die letzten zwei Operatoren sind binär, so dass φ U ψ eine syntaktisch korrekte Formel ist, wenn φ und ψ syntaktisch korrekte Formeln sind.
Semantik
Eine LTL-Formel kann sowohl über einer unendlichen Sequenz von Aussagen als auch einer einzigen Position auf dem Pfad ausgewertet werden. Eine LTL-Formel ist genau dann auf einem Pfad erfüllt, wenn sie auf Position 0 des Pfades erfüllt ist. Die Semantik der modalen Operatoren ist wie folgt.
Textform Symbol Erklärung Beispielpfad Einstellige Verknüpfungen: X φ 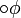
nächster: φ gilt am nächsten Zustand. 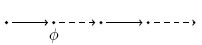
G φ 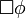
Global: φ gilt auf dem kompletten nachfolgenden Pfad. 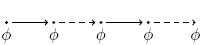
F φ 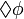
Finally: φ gilt irgendwann auf dem nachfolgenden Pfad. 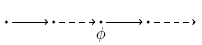
Zweistellige Verknüpfungen: ψ U φ 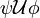
Until: φ gilt an der aktuellen oder einer nachfolgenden Position und ψ gilt solange bis diese Position erreicht ist. An dieser Position muss ψ nicht mehr gelten. 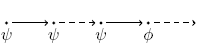
ψ R φ 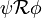
Release: φ gilt bis zur ersten Position, an der ψ gilt oder für immer, wenn eine solche Position nicht existiert. 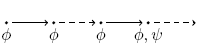
Bereits zwei der Operatoren sind fundamental, d. h. sie definieren die anderen indem sie verknüpft werden:
- F φ = true U φ
- G φ = false R φ =
 F
F  φ
φ - ψ R φ =
 (
( ψ U
ψ U  φ)
φ)
Sonderverknüpfungen
Einige Autoren definieren einen schwachen bis-Operator (weak until, mit W bezeichnet), der eine ähnliche Semantik wie der bis-Operator besitzt, jedoch keine Haltebedingung erforderlich ist. Manchmal ist es sinnvoll wenn U und R mit Formeln des schwachen bis-Operators definiert werden können:
- ψ U φ = F φ
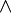 (ψ W φ)
(ψ W φ) - ψ R φ = φ W (ψ
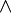 φ)
φ) - φ W ψ = ψ R (ψ
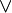 φ)
φ) - φ W ψ = (φ U ψ
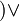 G φ
G φ
Wichtige Eigenschaften
Es gibt zwei Eigenschaften die der linearen temporalen Logik zugeschrieben werden: Sicherheit (safety), sagt aus dass etwas unerwünschtes nie auftritt (G
 φ) und Lebendigkeit (liveness), was aussagt dass etwas erwünschtes immer wieder passiert (GFψ oder G
φ) und Lebendigkeit (liveness), was aussagt dass etwas erwünschtes immer wieder passiert (GFψ oder G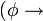 Fψ)). Generell: Sicherheit ist eine Eigenschaft für welche ein Gegenbeispiel ein endliches Präfix besitzt, selbst wenn der zu untersuchende Pfad unendlich ist. Für die Lebendigkeit wiederum kann jedes endliche Präfix eines Gegenbeispiels zu einem unendlichen Pfad verlängert werden, das die Formel erfüllt.
Fψ)). Generell: Sicherheit ist eine Eigenschaft für welche ein Gegenbeispiel ein endliches Präfix besitzt, selbst wenn der zu untersuchende Pfad unendlich ist. Für die Lebendigkeit wiederum kann jedes endliche Präfix eines Gegenbeispiels zu einem unendlichen Pfad verlängert werden, das die Formel erfüllt.Äquivalenzumformungen
Folgende Äquivalenzumformungen sind möglich:
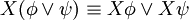
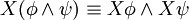
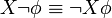
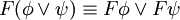
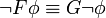
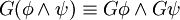
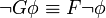
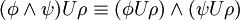
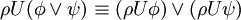
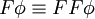
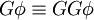
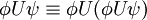
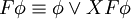
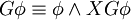
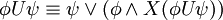
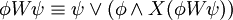
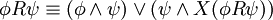
Beziehungen zu anderen Logiken
Lineare temporale Logik (LTL) ist eine Teilmenge der Computation Tree Logic* (CTL*), besitzt eine gemeinsame Teilmenge mit CTL ist jedoch weder Ober- noch Untermenge von CTL.
LTL ist äquivalent zur Prädikatenlogik mit einem Nachfolger und der kleiner-Relation, FO[S,<] wie auch stern-freien regulären Ausdrücken oder deterministischen endlichen Automaten mit einer Schleifenkomplexität von 0.
Automata theoretic Linear temporal logic model checking
Ein wichtiger Weg zur Modellprüfung ist die gewünschten Eigenschaften (wie oben beschrieben) mit LTL-Operatoren zum Ausdruck zu bringen und tatsächlich überprüfen, ob das Modell diese Eigenschaft erfüllt.
Eine Möglichkeit ist es einen zum Modell "äquivalenten" Büchi-Automaten zu erstellen und einen, der zur Negation äquivalent ist. Der Schnitt der beiden nicht-deterministischen Büchi-Automaten ist leer, wenn das Modell die Eigenschaften erfüllt.
Siehe auch: Computation Tree Logic (CTL)
Weblinks
- P. Gumm - Lineare temporale Logik von der Universität Marburg
- A presentation of LTL (englisch)
- Linear-Time Temporal Logic and Büchi Automata (englisch)
Wikimedia Foundation.
