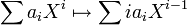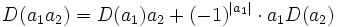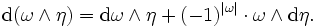Antiderivation

In verschiedenen Teilgebieten der Mathematik bezeichnet man Abbildungen als Derivationen, wenn sie die Leibnizregel erfüllen. Das Konzept der Derivationen ist eine Verallgemeinerung der aus der Schulmathematik bekannten Ableitung.

Definition

Es sei R ein kommutativer Ring mit Eins, beispielsweise ein Körper wie $\mathbb R$ oder $\mathbb C$. Weiter sei A eine assoziative R-Algebra und M ein A-A-Bimodul. Eine (R-lineare) Derivation von A mit Werten in M ist eine R-lineare Abbildung 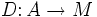$D\colon A\to M$, die

D(a₁a₂) = D(a₁)a₂ + a₁D(a₂) für alle $a_1,a_2\in A$

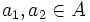
erfüllt.

Wichtige Spezialfälle sind:

• A selbst ist auf kanonische Weise ein A-A-Bimodul.
• Ist A kommutativ, so ist jeder A-Modul auf kanonische Weise ein A-A-Bimodul.

Im Spezialfall M = A kann die definierende Gleichung direkt als Gleichung in A gelesen werden. Auf diese Weise kann der Begriff der A-wertigen Derivation auf nicht assoziative Algebren verallgemeinert werden.

Allgemeine Eigenschaften

• Ist A eine Algebra mit Einselement, so gilt D(r) = 0 für alle $r\in R$.
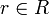• Der Kern einer Derivation ist eine Unteralgebra.
• Die Menge der Derivationen von A mit Werten in A bildet mit dem Kommutator eine Liealgebra: Sind D₁ und D₂ Derivationen, so auch

$[D_1,D_2]=D_1\circ D_2-D_2\circ D_1.$

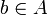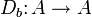• Für ein Element $b\in A$ ist $D_b\colon A\to A$, D_b(a) = ba − ab, eine Derivation. Derivationen dieses Typs heißen innere Derivationen. Die Hochschild-Kohomologie H²(A,A) ist der Quotient des Moduls der Derivationen nach dem Untermodul der inneren Derivationen.
• Ist A kommutativ, so gilt D(aⁿ) = na^{n − 1}D(a) für nichtnegative ganze Zahlen n.

Beispiele

• Für A = R[X] ist die formale Ableitung

$\sum a_i X^i \mapsto \sum i a_i X^{i-1}$

eine R-lineare Derivation von A mit Werten in A.

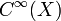• Sei X eine Mannigfaltigkeit. Dann ist die Cartan-Ableitung eine $\mathbb R$-lineare Derivation von $C^\infty(X)$ mit Werten im Raum A¹(X) der 1-Formen auf X.
• Eine der Umformulierungen der Jacobi-Identität für Liealgebren besagt, dass die adjungierte Darstellung durch Derivationen operiert:

[X,[A,B]] = [[X,A],B] + [A,[X,B]].

Derivationen und Kähler-Differentiale

Per definitionem werden R-lineare Derivationen einer kommutativen Algebra A durch den Modul Ω_{A / R} der Kähler-Differentiale klassifiziert, d.h. es gibt eine natürliche Bijektion zwischen den R-linearen Derivationen von A mit Werten in einem A-Modul M und den A-linearen Abbildungen 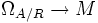$\Omega_{A/R}\to M$. Jede Derivation 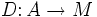$D\colon A\to M$ entsteht als Verkettung der universellen Derivation 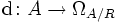$\mathrm d\colon A\to\Omega_{A/R}$ mit einer A-linearen Abbildung $\Omega_{A/R}\to M$.

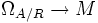Antiderivationen

Definition

Ist A eine 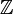$\mathbb Z$- oder 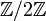$\mathbb Z/2\mathbb Z$-graduierte R-Algebra, so heißt eine R-lineare graduierte Abbildung 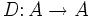$D\colon A\to A$ eine Antiderivation, wenn

$D(a_1a_2)=D(a_1)a_2+(-1)^{|a_1|}\cdot a_1D(a_2)$

für alle homogenen Elemente 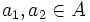$a_1,a_2\in A$ gilt; dabei bezeichnet | a₁ | den Grad von a₁.

Beispiele

• Die äußere Ableitung von Differentialformen ist eine Antiderivation:

$\mathrm d(\omega\wedge\eta)=\mathrm d\omega\wedge\eta+(-1)^{|\omega|}\cdot\omega\wedge\mathrm d\eta.$