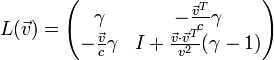- Lorentzboost
-
Die spezielle Lorentztransformation (auch Boost genannt) dient dazu, entsprechend der speziellen Relativitätstheorie von einem Koordinatensystem in ein anderes umzurechnen, wenn sich die beiden relativ zueinander mit einer konstanten Geschwindigkeit bewegen.
Das Koordinatensystem, in dem das zu beschreibende Objekt ruht, wird Ruhesystem genannt.
Die Operation
 wechselt in das Koordinatensystem, das sich relativ zum Ruhesystem mit der Geschwindigkeit
wechselt in das Koordinatensystem, das sich relativ zum Ruhesystem mit der Geschwindigkeit  bewegt. Mit
bewegt. Mit  kann vom bewegten in das Ruhesystem zurückgerechnet werden. (Leider sind da die Notationen nicht ganz einheitlich, es kann also durchaus vorkommen, dass bei
kann vom bewegten in das Ruhesystem zurückgerechnet werden. (Leider sind da die Notationen nicht ganz einheitlich, es kann also durchaus vorkommen, dass bei  ein anderes Vorzeichen auftritt!)
ein anderes Vorzeichen auftritt!)
Für einen Boost in Richtung lautet die Transformation in Matrixdarstellung
lautet die Transformation in Matrixdarstellung 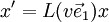 mit
mit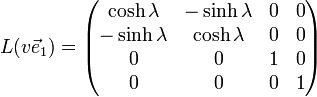 und
und 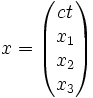 ,
,
wobei λ hier die Rapidität ist, die durch
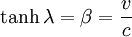 definiert ist, also coshλ = γ und
definiert ist, also coshλ = γ und 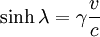 mit
mit 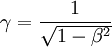 .
.Allgemein ist der Boost (ins Ruhesystem eines sich mit der Geschwindigkeit
 bewegenden Teilchens) durch
bewegenden Teilchens) durchgegeben, wobei I die Einheitsmatrix ist. Man erhält diese Darstellung, wenn man den Vektor
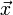 in die senkrechte und parallele Komponente bezüglich des Geschwindigkeitsvektors
in die senkrechte und parallele Komponente bezüglich des Geschwindigkeitsvektors 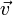 zerlegt:
zerlegt: 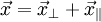 . Dann bleibt die senkrechte Komponente
. Dann bleibt die senkrechte Komponente 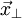 unverändert, während die parallele Komponente
unverändert, während die parallele Komponente 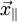 entsprechend der obigen Formel für die 1-Richtung transformiert:
entsprechend der obigen Formel für die 1-Richtung transformiert: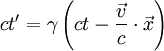
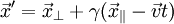 .
.
Beachte: Die spezielle Lorentztransformation wechselt nur zwischen Koordinatensystemen. Sie ist keine Beschleunigung oder ähnliches! So gesehen ist die Bezeichnung Boost irreführend!Eigenschaften
- Die Lorentztransformationen bezüglich einer festen Richtung für
 bilden eine Untergruppe der Lorentz-Gruppe in Analogie zu den Drehungen um eine feste Achse, welche eine Untergruppe der Drehgruppe bilden.
bilden eine Untergruppe der Lorentz-Gruppe in Analogie zu den Drehungen um eine feste Achse, welche eine Untergruppe der Drehgruppe bilden. - Die Gesamtheit der speziellen Lorentztransformationen bilden keine Untergruppe der Lorentz-Gruppe. Dies wird durch den Kommutator der Erzeugenden ersichtlich: [Ki,Kj] = − εijkLk, wobei Ki die Erzeugenden der speziellen Lorentztransformation sind und Lk die der Drehgruppe. (Im Gegensatz dazu bilden die Drehungen eine Untergruppe der Lorentz-Gruppe.)
- Um die Untergruppe vollständig zu machen müssen die Drehungen dazugenommen werden. Zusammen ergeben sie dann die eigentliche orthochrone Lorentzgruppe.
Wikimedia Foundation.