Lyot-Filter

Das nach seinem Erfinder, dem französischen Astronomen Bernard Ferdinand Lyot, benannte Lyot-Filter ist ein optisches Filter, das Doppelbrechung nutzt, um einen schmalen Durchlassbereich der übertragenen Wellenlängen zu erzeugen. Der Anwendungsbereiche des Lyot-Filters sind die Astronomie, die Laserphysik, um durchstimmbare Laser zu realisieren, sowie die optische Datenübertragung.

Aufbau

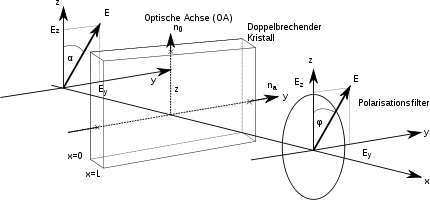
Ein Lyot-Filter besteht aus einem doppelbrechenden Kristall, normalerweise Quarz, und einem nachfolgendem Polarisationsfilter. Um den freien Spektralbereich zu erhöhen werden mehrere Lyot-Filter hintereinander geschaltet. Dabei wird die Dicke der Platten bei jedem nachfolgenden Filter halbiert.

Physikalisches Prinzip

Prinzipskizze eines Lyot-Filters. Zur Erklärung siehe Text

Auf Grund der doppelbrechenden Eigenschaften der Platten weisen die ordentlichen und außerordentlichen Komponenten eines Lichtstrahls einen unterschiedlichen Brechungsindex auf und besitzen deshalb eine unterschiedliche Phasengeschwindigkeit. Dies führt für unterschiedliche Wellenlänge auf unterschiedliche Phasendifferenzen δ zwischen ordentlichem und außerordentlichem Strahl. Nimmt man an, dass linear polarisiertes Licht auf den Filter trifft, so wird das Licht durch die Platte im Allgemeinen elliptisch polarisiert. Nur wenn die Phasendifferenz beider Teilstrahlen $\delta=m\cdot 2\pi$ entspricht, ist das Licht hinter dem Filter wieder in gleicher Weise linear polarisiert (m ist eine natürliche Zahl). Dies ist nur bei bestimmten Wellenlängen der Fall:
Die Feldstärke $\vec{E}(x,t)=\vec{E}_0\cos(\omega t-kx)$ wird in die Komponente parallel zur optischen Achse (ordentlicher Strahl) und senkrecht zur optischen Achse (außerordentlicher Strahl) zerlegt
$\vec{E_0}=E_{0}\cos(\alpha)\vec{e}_z+E_{0}\sin(\alpha)\vec{e}_y=E_{0z}\vec{e}_z+E_{0y}\vec{e}_y.$
Wenn der doppelbrechende Kristall so in den Strahlengang gestellt wird, dass er bei x = 0 beginnt und bei x = L endet und seine optische Achse mit der z-Achse übereinstimmt, so wird die Feldstärke hinter dem Kristall durch
$\vec{E}(t,L)=E_{0z}\cos(\omega t-k n_0L)\vec{e}_z+E_{0y}\cos(\omega t-k n_a L)\vec{e}_y$
beschrieben. Dabei ist k die Wellenzahl und n₀ der Brechungsindex des ordentlichen Strahls sowie n_a der Brechungsindex des außerordentlichen Strahls
Durch Vergleich mit der Feldstärke vor dem Auftreffen auf den Kristall folgt die Phasendifferenz der beiden Teilstrahlen:
$\delta=k(n_0 -n_a)L=\frac{2\pi}{\lambda}(n_0-n_a)L.$
Das Licht ist nach dem Durchlauf durch den Kristall nur im gleichen Polarisationszustand wie beim Einfall, wenn $\delta=m\cdot2\pi$ gilt.
Dies ist gleichbedeutend mit der Forderung
$\frac{2\pi}{\lambda}(n_0-n_a)L=m 2\pi$
$\Leftrightarrow \lambda=\frac{L(n_0-n_a)}{m}.$
Der nachfolgende Polarisationsfilter schwächt also alle Anteile des Lichts, die nicht diese Wellenlänge haben. Der Lyot-Filter ist also ein wellenlängenabhängiger optischer Filter.
Sei nun φ, der Winkel des Polarisationsfilters, so eingestellt, dass das linear polarisierte Licht $\vec{E}$ optimal durchgelassen wird. Wenn nun der Polarisationsfilter um φ gedreht wird, so wird nur noch die Komponente $|\vec{E}|\cdot \cos(\varphi)$ durchgelassen bzw. die Intensität
$I=|\vec{E}|^2\cos^2(\varphi)$ Außerdem sei nun I die Intensität des Lichts hinter und I₀ die Intensität vor dem Lyot-Filter.
Die Transmission $T=\frac{I}{I_0}=\frac{|\vec{E}|^2}{|\vec{E}_0|^2}$ ergibt sich nach kurzer Rechnung (mit Hilfe von Additionstheoremen bzw. zur einfacheren Rechnung Welle als e^{i(ωt − kx)} annehmen anstatt cos(ωt − kx)) zu
$T(\lambda)=\cos^2\left(\frac{\pi L(n_0-n_a)}{\lambda}\right)$
bzw.
$T(\nu)=\cos^2\left(\frac{\pi L(n_0-n_a)\nu}{c}\right).$
Der freie Spektralbereich Δν ergibt sich aus dem Abstand zweier Maxima zu
$\Delta \nu=\frac{L\nu(n_0-n_a)}{c}.$

Hintereinander geschaltete Lyot-Filter

Die totale Transmission von M hintereinander geschalteten Filtern ergibt sich aus den Einzeltransmissionen T_m
$T_{tot}(\lambda)=\prod \limits_{m=1}^{M}T_m(\lambda).$
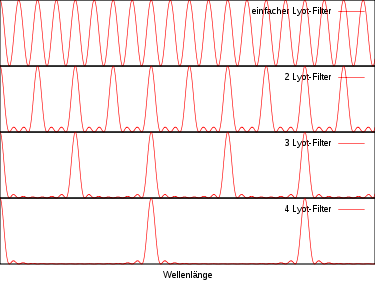
Im nebenstehenden Bild wurden vier Lyot-Filter hintereinander angewendet. Dabei wurde die Dicke der Platten (doppelbrechender Kristall) bei jedem weiteren Filter halbiert.

Transmission hintereinandergeschalteter Lyot-Filter. Die Dicke des doppelbrechenden Kristalls halbiert sich bei jedem nachfolgendem Filter

Durchstimmbarkeit des Lyot-Filters

Die durchgelassenen Wellenlängen eines Lyot-Filters sind durch L, die Dicke des Kristalls und n₀ bzw. n_a, die Brechungsindizes des ordentlichen und außerordentlichen Strahls des doppelbrechenden Materials, festgelegt. Werden diese Parameter verändert, so ändert sich der Durchlassbereich des Filters.
Am einfachsten lässt sich der Lyot-Filter verstimmen, indem der Kristall um die z-Achse gedreht wird, was zu einer Änderung von L führt. Handelt es sich beispielsweise um einen würfelförmigen Kristall, so ist L minimal wenn das Licht senkrecht auf eine Seitenfläche trifft. Wird der Kristall um die z-Achse gedreht, so muss das Licht eine größere Strecke im Kristall durchlaufen, was zu einer Änderung der Phasendifferenz der beiden Teilstrahlen führt und damit zu einer Änderung des Durchlassbereiches des Filters.
Durch Drehung des Kristalls um den Winkel $\vartheta$ um die x-Achse, verändert sich das Transmissionsmaximum $\lambda_m=\frac{L(n_0-n_a)}{m}$ des Lyot-Filters, da n₀ unabhängig aber n_a abhängig von $\vartheta$ ist (Brechungsindexellipsoid). Die Verwendung von elektrisch veränderbaren Doppelbrechungselementen (z.B. Flüssigkristallen) ergibt ein „elektrisch abstimmbares Lyot-Filter“. Durch Variation der Feldstärke eines äußeren elektrischen Feldes ändert sich der Brechungsindex spezieller Kristalle wie KDP (Kaliumdihydrogenphosphat) durch den elektro-optische Effekt. Dies führt wiederum zu einem verstimmbaren Lyot-Filter, wobei der durchstimmbare Bereich klein ist.

Literatur

• Wolfgang Demtröder: Laserspektroskopie - Grundlagen und Technik. Springer-Verlag 2000, 4. Auflage, ISBN 3-540-64219-6