Brechungsindex

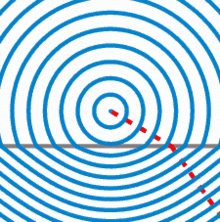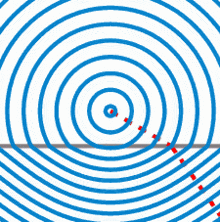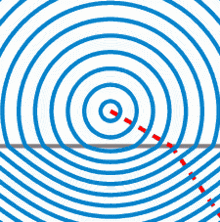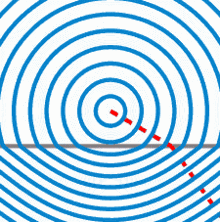Wellenfronten, die von einem Punkt ausgehen, beim Übergang in ein Medium mit einem höheren Brechungsindex. Die Phasengeschwindigkeit der Welle ist unterhalb des grauen Strichs niedriger. Die oben exakt kugelförmigen Wellenfronten sind unten nicht mehr kugelförmig, sondern nahezu hyperbolisch. Diesen Effekt kennt man vom Blick in ein Wasserbecken, der Grund erscheint nicht nur angehoben, sondern zusätzlich gekrümmt.

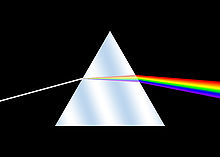Der Brechungsindex von Glas hängt von der (Vakuum-)Wellenlänge ab (Dispersion). Deshalb wird weißes Licht in seine Spektralfarben zerlegt.

Der Brechungsindex, auch die Brechzahl, ist eine optische Materialeigenschaft. Diese physikalische dimensionslose Größe gibt an, um welchen Faktor die Wellenlänge und die Phasengeschwindigkeit des Lichts kleiner sind als im Vakuum.

An der Grenzfläche zweier Medien mit unterschiedlichem Brechungsindex wird Licht gebrochen und reflektiert. Dabei nennt man das Medium mit dem höheren Brechungsindex das optisch dichtere. Dies ist nicht zu verwechseln mit der „optischen Dichte“ als Maß für die Extinktion.

Physikalische Grundlagen

Einfluss des komplexen Brechungsindex eines Materials (n₁ + ik₁) auf das Reflexionsverhalten eines Lichtstrahls beim Auftreffen auf die Grenzfläche Luft/Material

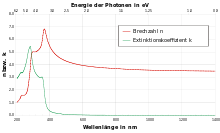Verlauf des wellenlängenabhängigen komplexen Brechungsindex im visuellen Bereich für einen Halbleiter mit Bandübergängen in diesem Bereich

Die Bezeichnung „Brechungsindex“ kommt vom Begriff Brechung und seinem Auftreten im Snelliusschen Brechungsgesetz. Der Brechungsindex n ist eine dimensionslose physikalische Größe, also eine reine Zahl: Er gibt das Verhältnis der Vakuumlichtgeschwindigkeit c₀ zur Ausbreitungsgeschwindigkeit c_M des Lichts im Medium an:

$n = \frac{c_0}{c_{\mathrm{M}}}$

Zur Berücksichtigung weiterer Effekte, wie der Absorption der Welle im Medium, kann der Brechungsindex auch als komplexe Zahl angegeben werden. Hierbei sind unterschiedliche Symboliken gängig:

$n(\omega) = n'(\omega) + \mathrm i \, n''(\omega) = n'(\omega) + \mathrm i \, k(\omega) = n' (\omega) \left[ 1 + \mathrm i \, \kappa(\omega) \right]$

wobei n(ω) die Lichtgeschwindigkeit im Medium bezeichnet, ω die Kreisfrequenz (2π·Frequenz) der Strahlung, k(ω) = n''(ω) den wellenlängenabhängigen Extinktionskoeffizienten und κ(ω) den wellenlängenabhängigen Absorptionsindex des Materials.

Der Brechungsindex ist frequenz- und damit auch wellenlängenabhängig. Dieser als Dispersion bezeichnete Effekt ermöglicht beispielsweise die Zerlegung von weißem Licht in seine Spektralfarben an einem Prisma. Die Frequenzabhängigkeit des (komplexen) Brechungsindex in Materie kann recht gut über das Modell des Lorentz-Oszillators beschrieben werden.

Absorptionskoeffizient und -index

Über den Extinktionskoeffizienten ist es möglich, die Extinktion, also die Schwächung von Strahlung beim Durchgang durch Materie, zu beschreiben.

Eine in das Medium in z-Richtung eindringende Welle (Wellenvektor $\vec{k}=k\,\hat{e}_z$) klingt gemäß exp( − n''ωz / c) exponentiell ab. Ersetzt man in

$\vec{E}=\vec{E}_{0}e^{i\left[ \vec{k}\cdot\vec{r}-\omega t \right]}=\vec{E}_{0}e^{i\left[ kz-\omega t \right]}$

die Kreiswellenzahl, die dem Betrag des Wellenvektors $k=|\vec{k}|$ (Vorsicht: Verwechslungsgefahr mit dem Extinktionskoeffizienten k = n'') gleich ist, mit

$k=\frac{\omega }{c_{0}}N=\frac{\omega }{c_{0}}(n'+\mathrm i n'' )$,

so erhält man das abklingende Verhalten (evaneszente Welle):

$\vec{E}=\vec{E}_{0}e^{\mathrm i\left[ (n'+\mathrm i n'' )\frac{\omega }{c_{0}}z-\omega t \right]}=\vec{E}_{0}e^{- n'' \frac{\omega}{c_{0}}z}e^{\mathrm i\left[n'\frac{\omega }{c_{0}}z-\omega t \right]}$

Man betrachtet weiterhin obige evaneszente Welle. Die Intensität $I\propto|E|^2$ nimmt also exponentiell ab

$I=I_{0}\,e^{-2 n'' \frac{\omega}{c_{0}} z}=I_{0}\,e^{-\alpha z}$

Dabei wurde der Absorptionskoeffizient $\alpha = 2 n'' \frac{\omega}{c_{0}}$ eingeführt.

Oft wird der Extinktionskoeffizient n'' fälschlicherweise mit dem Absorptionskoeffizienten α oder dem Absorptionsindex κ gleichgesetzt. Sie lassen sich jedoch ineinander umwandeln, es gilt:

$\frac{\alpha c_0}{2\omega}= n'' = n'\kappa$

wobei c₀ die Vakuumlichtgeschwindigkeit und ω = 2πν die Kreisfrequenz des Lichtes ist.

Permittivitätszahl

Der komplexe Brechungsindex ist mit der Permittivitätszahl (dielektrische Funktion) $\varepsilon_r$ und der Permeabilitätszahl μ_r verknüpft.

$n=\sqrt{\varepsilon_r \mu_r }$

Dabei sind alle Größen im Allgemeinen komplex und frequenzabhängig.

Wenn man die Wellenlängenabhängigkeit (Dispersion) des Brechungsindex eines Materials theoretisch ermitteln will, geht man über die elektrische Suszeptibilität, die die Beiträge der verschiedenen Mechanismen im Material zu den Eigenschaften erfasst und in der komplexen Permittivität mündet. Im Fall von nichtmagnetischen Material ist $\mu_r \approx 1$ und der komplexe Brechungsindex kann direkt aus Real- (ε₁) und Imaginärteil (ε₂) der Permittivitätszahl angegeben werden:

$n=\sqrt{\varepsilon_r }=\sqrt{{\varepsilon }_{1}+\mathrm i{\varepsilon }_{2}}$

Hieraus kann man die Größen n und k berechnen:

$n^2 = \frac{1}{2} \left(\sqrt{{\varepsilon_1}^2 + {\varepsilon_2}^2} + \varepsilon_1\right)$

$k^2 = \frac{1}{2} \left(\sqrt{{\varepsilon_1}^2 + {\varepsilon_2}^2} - \varepsilon_1\right)$

Gruppenbrechungsindex

Das Verhältnis der Vakuumlichtgeschwindigkeit c₀ und der Gruppengeschwindigkeit c_g des Lichts im Medium ist der Gruppenbrechungsindex n_g. Diese von der Wellenlänge λ des Lichts abhängige Materialeigenschaft wird auch Gruppenbrechungsindex genannt.

$n_\mathrm{g}(\lambda) = \frac{c_0}{c_\mathrm{g}(\lambda)}$

Die Gruppengeschwindigkeit hat im Vakuum den gleichen Wert wie die Phasengeschwindigkeit. Zudem ist dieser Wert unabhängig von der Wellenlänge des Lichts. Im Medium ist das nicht notwendigerweise der Fall. Besonders bei Wellenlängen, für die das Material große Dispersion zeigt, ergeben sich Unterschiede.

Andere Definitionen

Brechung

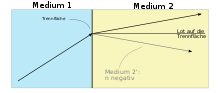
Die Definition des Brechungsindex erfolgte oben über die Geschwindigkeit, mit der sich Licht im Material ausbreitet. Dieses Vorgehen ist naheliegend, aber nicht in allen Fällen anwendbar. Beispielsweise können Meta-Materialien dem geometrischen Strahlengang nach einen negativen Brechungsindex aufweisen. Ein negativer Wert der Lichtgeschwindigkeit ist jedoch nicht sinnvoll definiert.

Alternative Definitionen des Brechungsindex bei denen dieses Problem nicht auftritt, sind:

• Über das Fermatsche Prinzip, nach welchem das Licht zwischen zwei Punkten jenen Weg zurücklegt, für den es einen Extremwert der Zeit benötigt.
• Über das Huygenssche Prinzip, das besagt, dass jeder Punkt einer Wellenfront als Ausgangspunkt einer Kugelwelle angesehen werden kann und die Interferenz aller dieser Wellen die weiter propagierende Wellenfront ergibt.
• Über die Strahlenoptik. Nach dem erwähnten Snellius-Brechungsgesetz entspricht n dem Sinus-Verhältnis von Einfallswinkel und gebrochenem Winkel.

Alle diese Definitionen liefern für gewöhnliche, optische Materialien den selben Wert.

Brechungsindex der Luft und anderer Stoffe

Brechungsindizes (Realteil) für ausgewählte Materialien im Bereich des sichtbaren Lichts
(wenn nicht anders angegeben λ=589 nm; n_D)

Material	Brechungsindex n
Vakuum	exakt 1
Luft (bodennah)	1,000292
Plasma	0 … 1
Caesium [1]	≈ 0,345 k ≈ 1,07
Aerogel	1,007 … 1,24
Eis	1,31
Wasser	1,33
menschl. Augenlinse	1,35 … 1,42
Ethanol[2] (liqu.)	1,3614
Magnesiumfluorid	1,38
Flussspat (Calciumfluorid)	1,43
menschliche Epidermis	1,45
Tetrachlorkohlenstoff (liqu.)	1,46
Quarzglas	1,46
Glyzerin	1,47399
Celluloseacetat (CA)	1,48
PMMA (Plexiglas™)	1,49
Benzol (liqu.)	1,49
Kronglas	≈ 1,46 … 1,65
Mikroskopische Deckgläser	1,523
COC (ein Kunststoff)	1,533
PMMI (ein Kunststoff)	1,534
Quarz	1,54
Halit (Steinsalz)	1,54
Polystyrol (PS)	1,58
Polycarbonat (PC)	1,585
Epoxidharz	≈ 1,55 … 1,63
Flintglas	≈ 1,56 … 1,93
Kohlenstoffdisulfid (liqu.)	1,63
Kunststoffglas für Brillen (phototrop)	bis 1,67 (1,60)
Diiodmethan (liqu.)	1,742
Rubin (Aluminiumoxid)	1,76
Mineralglas für Brillen (polarisierend)	bis 1,9 (1,5)
Glas	1,45 … 2,14
Bleikristall	bis 1,93
Zirkon	1,92
Schwefel	2,00
Zinksulfid	2,37
Diamant	2,42
Titandioxid (Anatas)	2,52
Siliciumcarbid	2,65 … 2,69
Titandioxid (Rutil)	3,10
Bleisulfid (PbS, 590 nm)	3,90

Größenordnungen

Vakuum hat einen Brechungsindex von exakt 1. Im sichtbaren Bereich sind die Brechungsindizes realer Materialien so gut wie immer größer als 1. Für jeden Stoff gibt es jedoch Wellenlängen (z. B. oberhalb des sichtbaren Bereiches), bei denen der Brechungsindex kleiner als 1 wird (aber positiv bleibt). Für sehr kleine Wellenlängen (Röntgenstrahlung, Gammastrahlung) ist der Brechungsindex immer kleiner als 1 und nähert sich mit sinkender Wellenlänge der 1 von unten an. Beispielsweise im Röntgenbereich ist die Darstellung n = 1 − δ üblich, wobei typische Werte für δ zwischen 10⁻⁹ und 10⁻⁵ liegen (stark abhängig von der Wellenlänge, abhängig von der Ordnungszahl und Dichte des Materials).

Luft

Der Brechungsindex der Luft beträgt auf Meeresniveau durchschnittlich 1,00029. Er hängt von der Dichte und damit von Temperatur der Luft ab, sowie von der speziellen Zusammensetzung der Luft – insbesondere der Luftfeuchtigkeit. Da die Luftdichte nach oben – entsprechend den Gasgesetzen in einem Schwerefeld – exponentiell abnimmt, siehe barometrische Höhenformel, beträgt er in etwa 8 km Höhe nur mehr 1,00011. Dennoch werden die von Sternen kommenden Lichtstrahlen in Horizontnähe um 0,6° gehoben und in 45° noch um 0,017°. Der Effekt heißt astronomische Refraktion und beeinflusst in ähnlicher Art auch jede terrestrische Vermessung. Im technischen Bereich wird manchmal zur Vereinfachung der Brechungsindex der Materialien auf den von Luft bezogen, ohne dass eine einheitliche Bezeichnung für diese leicht abweichenden Werte etabliert wäre.

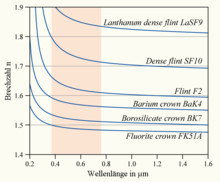
Wellenlängenabhängigkeit

Der Brechungsindex einiger Glassorten als Funktion der Wellenlänge. Der sichtbare Bereich ist rot markiert.

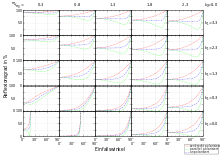
Da wie in der Einleitung beschrieben der Brechungsindex jedes Materials von der Wellenlänge des einfallenden Lichts abhängt – gilt auch bei elektromagnetischen Strahlungen anderer Wellenlängebereiche – wäre es notwendig, diesen auch wellenlängenabhängig (tabellarisch oder als Funktion) anzugeben. Da dies aber für viele einfache Anwendungen nicht notwendig ist, wird der Brechungsindex üblicherweise für die Wellenlänge der Natrium-D-Linie (589 nm) angegeben. In der linken Abbildung sind als Beispiel Kurven des wellenlängenabhängigen Brechungsindex einiger Glassorten dargestellt. Sie zeigen den typischen Verlauf einer normalen Dispersion.

Messung

Zur experimentellen Bestimmung des Brechungsindex eines Mediums mit $\mu_{r2}\ (\mbox{med})=\mu_{r1}\ (\mbox{Luft})$ (zum Beispiel nicht magnetisch) n_med kann man zum Beispiel den Brewster-Winkel beim Übergang von Luft in dieses Medium messen. Für diesen Fall gilt $\tan (\alpha_{\rm Brewster}) = \frac{n_{\rm med}}{n_{\rm Luft}} \approx n_{\rm med}$. Für die Messung wird ein Refraktometer angewandt.

Eine Abschätzung des Brechungsindexes ist mit der sogenannten Immersionsmethode durch das Eintauchen eines Gegenstands in durchsichtige Flüssigkeiten mit verschiedener Dichte möglich. Wenn der Brechungsindex von Gegenstand und Flüssigkeit identisch sind, verschwinden die Konturen des Gegenstands. Dieses Verfahren kann leicht eingesetzt werden, um zum Beispiel Rubine oder Saphire mit einem Brechungsindex von rund 1,76 zu identifizieren, indem sie in eine geeignete Schwerflüssigkeit eingetaucht werden, wie beispielsweise Diiodmethan (Brechungsindex = 1,74).

Anwendung

Der Brechungsindex ist eine der zentralen Bestimmungsgrößen für optische Linsen. Die Kunst der Optikrechnung zur Auslegung optischer Instrumente (Objektive, Messinstrumente) beruht auf der Kombination verschiedener brechender Linsenoberflächen mit passenden Glassorten.

In der Chemie wird der Brechungsindex bei einer bestimmten Temperatur oft eingesetzt, um flüssige Substanzen zu charakterisieren. Die Temperatur und die Wellenlänge, bei der der Brechungsindex bestimmt wurde, werden dabei dem Symbol für den Brechungsindex angefügt, für 20 °C und die Natrium-D-Linie z. B. $n_D^{20}$.

Die Bestimmung des Brechungsindex erlaubt eine einfache Bestimmung des Gehaltes einer bestimmten Substanz in einem Lösungsmittel:

• Zucker in Wein, siehe Grad Brix und Grad Oechsle
• Harz in Lösungsmittel
• Gefrierschutzmittel (meist Ethylenglycol) im Kühlwasser von Verbrennungsmotoren oder thermischen Solaranlagen

Mikroprozessoren werden mittels Photolithographie hergestellt. Die Ätzmaske wird dabei durch ultraviolettes Licht einer Wellenlänge von 193 Nanometern übertragen. Normalerweise sind die kleinstmöglichen Abmessungen durch die halbe Wellenlänge begrenzt. Durch Einsatz von Flüssigkeiten mit einem Brechungsindex von 1,6 gelang es, ein Gitter paralleler Linien einer Dicke von nur 29,9 Nanometern zu erzeugen. Dadurch ist bei der Chipherstellung eine zukünftige weitere Steigerung unter Verwendung der gleichen Lichtquelle möglich.^[3][4]

Zusammenhang mit dem atomaren Aufbau des Materials

Beziehung zwischen Brechungsindex und Dichte für Silikat- und Borosilikatgläser.^[5]

Der Brechungsindex eines Materials hängt direkt mit seinem atomaren Aufbau zusammen. Der Grad der Kristallinität und das Kristallgitter eines Festkörpers wirken sich auf dessen Bandstruktur und somit auf den Brechungsindex aus. Im sichtbaren Spektrum zeigt sich dies beispielsweise bei der Verschiebung der Bandlücke. Durch einen anisotropen Kristallaufbau können zusätzlich Effekte wie die Doppelbrechung entstehen, bei dem das Material für unterschiedlich polarisiertes Licht abweichende Brechungsindizes besitzt.

Bei teilkristallinen oder amorphen Materialien hat der atomare Aufbau ebenfalls deutlichen Einfluss auf den Brechungsindex. So erhöht sich in der Regel der Brechungsindex von Silikat- und Borosilikatgläsern mit ihrer Dichte. Zum Beispiel haben Bleisilikatgläser mit hoher Dichte auch einen hohen Brechungsindex. Es gilt jedoch zu beachten, dass trotz des allgemeinen Trends die Beziehung zwischen Brechungsindex und Dichte nicht immer linear ist und dass Ausnahmen auftreten, wie links im Diagramm dargestellt. Einen relativ großen Brechungsindex und eine kleine Dichte kann man mit Gläsern erhalten, die leichte Metalloxide wie Li₂O oder MgO enthalten, während das Gegenteil mit PbO- und BaO-haltigen Gläsern erreicht wird.

Negative Brechungsindizes

1964 sagte der sowjetische Physiker Victor Veselago die Existenz von Materialien mit negativen Brechungsindizes voraus.

2002 gelang es Forschern um S. Sridhar von der Northeastern University in Boston, einen Verbundwerkstoff herzustellen, der ein feines Gitter aus Metalldrähten enthält, das für Mikrowellen einen negativen Brechungsindex zeigt.^[6]

2003 hat eine Gruppe um Yong Zhang in Colorado entdeckt, dass Kristalle aus Yttrium-Vanadat (YVO₄), einer Verbindung von Yttrium, Vanadium und Sauerstoff, auch ohne Weiterverarbeitung einen negativen Brechungsindex für Lichtwellen eines großen Frequenzbereichs aufweisen.^[7] Der Kristall besteht aus zwei ineinandergeschachtelten Kristallgittern mit symmetrischen optischen Achsen. Die negative Lichtbrechung tritt aber nur in einem gewissen Winkelbereich des Einfallswinkels auf. In künftigen Experimenten wollen die Forscher weitere vermutete Eigenschaften der negativen Brechung prüfen – wie etwa die Umkehrung des Dopplereffekts und der Tscherenkow-Strahlung.^[8]

2007 stellten Vladimir Shalaev und seine Kollegen von der Purdue-Universität ein Metamaterial mit negativem Brechungsindex für Strahlung im nahen Infrarotbereich vor.^[9]

2007 ist es Physikern um Ulf Leonhardt von der Universität St Andrews unter Verwendung von Metamaterial mit negativem Brechungsindex („linkshändiges Material“) gelungen, den sogenannten Casimir-Effekt umzukehren (reverser Casimir-Effekt, auch Quanten-Levitation genannt). Dies eröffnet die Zukunftsperspektive auf eine (nahezu) reibungslose Nanotechnologie.^[10][11]

Perfekte Linsen

Forscher um Prof. Xiang Zhang an der Universität Berkeley nutzten den in einem 35 Nanometer dünnen Silberfilm an der Grenzfläche zu PMMA auftretenden negativen Brechungsindex, um ein Mikroskop zu bauen, das eine sechsfach höhere Auflösung besitzt als die Wellenlänge des zur Beobachtung verwendeten Lichts.^[12]

In fernerer Zukunft könnte die Herstellung perfekter Linsen aus Metamaterialien gelingen, die kleinere Objekte als das Beugungslimit der Optik abbilden können. In der populärwissenschaftlichen Literatur findet man zu diesem Thema immer wieder die Aussage „Würde die Herstellung eines solchen Materials gelingen, könnte man damit Linsen herstellen, deren Auflösungsvermögen weit besser wäre als das von Linsen aus gewöhnlichen optischen Werkstoffen“.^[13] Die Einschränkung dabei ist, dass sich die Linse im Nahfeld (für Licht: <1 µm) des Objekts befinden muss, damit die evaneszente Welle noch nicht zu stark abgeklungen ist. Dies schränkt die Anwendung solcher Metamaterialien bisher auf die Mikroskopie ein. Ein verwandtes Verfahren ist die optische Rasternahfeldmikroskopie, die auf einem ähnlichen Grundprinzip (direkte Auswertung der evaneszenten Welle) beruht.

Literatur

• Michael Bass: Handbook of Optics Volume 1. Optical Techniques and Design:. 2. Auflage. Mcgraw-Hill Professional, 1994, ISBN 007047740X.
• Martin Roß-Meßemer: Den kleinsten Winkel im Visier. In: Innovation. Nr. 10, 2001, S. 22–23 (PDF-Datei; 705 kB, abgerufen am 20. Dezember 2009).
• Schott Glass (Hrsg.): Optical Glass Properties. 2000 (Produktkatalog; Brechungsindizes verschiedener Glassorten; PDF-Datei; 257 kB).

Weblinks

 Wiktionary: Brechungsindex – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Commons: Brechung – Sammlung von Bildern, Videos und Audiodateien

• Stefan Maier: Forscher: Negativer Brechungsindex existiert. www.wissenschaft.de. 19. März 2003, abgerufen am 20. Dezember 2009 (Negativer Brechungsindex bei Mikrowellen).
• Stefan Maier: Forscher: Gewöhnlicher Kristall hat negativen Brechungsindex. www.wissenschaft.de. 23. Oktober 2003, abgerufen am 20. Dezember 2009.
• Stefan Maier: Verkehrte Welt wird (beinahe) sichtbar. www.wissenschaft.de. 23. Juli 2007, abgerufen am 20. Dezember 2009 (Metamaterial mit negativem Brechungsindex im nahen Infrarotbereich).
• C. Wolfseher: Brechung. Abgerufen am 20. Dezember 2009 (Dynamische Arbeitsblätter mit Geogebra).
• Belle Dumé: The speed of light is not violated by negative refraction. PhysicsWeb, 20. März 2003, abgerufen am 20. Dezember 2009.
• Datenbank für Brechungsindizes und Absorptionskoeffizienten. Filmetrics (Hrsg), abgerufen am 4. August 2011.
• RefractiveIndex.INFO – Datenbank für Brechungsindizes. Mikhail Polyanskiy (Hrsg), abgerufen am 20. Dezember 2009.
• TexLoc Refractive Index of Polymers. (engl.), abgerufen am 27. August 2010

Einzelnachweise

1. ↑ H. Steffen, H. Mayer: Optische Eigenschaften dünner Cäsium-Schichten im Wellenlängenbereich von 0,3 bis 0,9 μ und ihr elektrischer Widerstand. In: Zeitschrift für Physik A Hadrons and Nuclei. 254, Nr. 3, 1. Mai 1972, S. 250–268, doi:10.1007/BF01379784.
2. ↑ David R. Lide (Hrsg.): CRC Handbook of Chemistry and Physics: A ready-reference book of chemical and physical data. 90. Aufl., CRC Taylor & Francis, Boca Raton Fla. 2009, ISBN 0-8493-0487-3, S. 3-232.
3. ↑ IBM beats optical lithography limits (Technology News in optics.org vom 22. Februar 2006)
4. ↑ Stefan Maier: Photolithographie ist noch lange nicht am Ende. (Newsticker wissenschaft.de vom 28. Februar 2006)
5. ↑ Glassproperties.com Berechnung des Brechungsindex von Gläsern (in englischer Sprache)
6. ↑ C. Kusko, Z. Zhai, N. Hakim, R. S. Markiewicz, S. Sridhar, D. Colson, V. Viallet-Guillen, A. Forget, Yu. A. Nefyodov, M. R. Trunin, N. N. Kolesnikov, A. Maignan, A. Daignere, A. Erb: Anomalous microwave conductivity due to collective transport in the pseudogap state of cuprate superconductors. In: Physical Review B. 65, Nr. 13, 6. Februar 2002, S. 132501, doi:10.1103/PhysRevB.65.132501.
7. ↑ Left Handed Material at Work. In: Physics News. Abgerufen am 20. Dezember 2009 (englisch). 
8. ↑ Yong Zhang, B. Fluegel, A. Mascarenhas: Total Negative Refraction in Real Crystals for Ballistic Electrons and Light. In: Physical Review Letters. 91, Nr. 15, 9. September 2003, S. 157404, doi:10.1103/PhysRevLett.91.157404.
9. ↑ V. M. Shalaev: Optical negative-index metamaterials. In: Nat. Photonics. 1, 2007, S. 41–48, doi:10.1038/nphoton.2006.49.
10. ↑ Rainer Scharf: Bisweilen stößt das Nichts auch ab. In: Frankfurter Allgemeine Zeitung. 11, 14. Januar 2009, S. N1.
11. ↑ Ulf Leonhardt et al: Quantum levitation by left-handed metamaterials. In: New J. Phys. 9, 2007, S. 254, doi:10.1088/1367-2630/9/8/254.
12. ↑ H. Lee, Y. Xiong, N. Fang, W. Srituravanich, S. Durant, M. Ambati, C. Sun, X. Zhang: Realization of optical superlens imaging below the diffraction limit. In: New J. Phys. 7, 2005, S. 255, doi:doi:10.1088/1367-2630/7/1/255 ([1]).
13. ↑ Victor G. Veselago: The electrodynamics of substances with simultaneously negative values of ε and μ. In: Sov. Phys. Usp. 10, Nr. 4, 1968, S. 509–514, doi:10.1070/PU1968v010n04ABEH003699.