Lücke-Theorem

Das Preinreich-Lücke-Theorem besagt, dass der Kapitalwert der Residualgewinne dem Kapitalwert der Zahlungsüberschüsse entspricht. Dies gilt natürlich nur, wenn die Unterschiede auf unterschiedlicher Periodisierung der Auszahlungen bzw. Einzahlungen gegenüber den Kosten und Leistungen beruhen. Das Theorem wurde von Wolfgang Lücke 1955 als Alternative zur Cash-Flow-basierten Investitionsrechnung vorgeschlagen und hielt damit Einzug in die deutsche Wirtschaftswissenschaft. Im US-amerikanischen Raum hingegen wurde sie bereits früher, nämlich 1937 von Gabriel Preinreich beschrieben.

Annahmen

Damit der aus den Einnahmen und Ausgaben eines Projekts berechnete Kapitalwert mit dem aus Ertrags- und Aufwandsgrößen ermittelten Kapitalwert übereinstimmt und damit zur gleichen optimalen Investitionsentscheidung führen kann, müssen folgende Bedingungen erfüllt sein:

Erstens muss die Summe der Zahlungsüberschüsse aller Perioden Z_t = EZ_t − AZ_t gleich der Summe aller Periodengewinne G_t sein:

$\sum_{t=0}^T G_t = \sum_{t=0}^T Z_t$

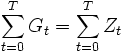
• G_t Periodengewinn zum Zeitpunkt t
• Z_t Einzahlungsüberschuss zum Zeitpunkt t
• EZ_t Einzahlungen zum Zeitpunkt t
• AZ_t Auszahlungen zum Zeitpunkt t
• T Laufzeit
• t jeweilige Periode

Dies entspricht dem Kongruenzprinzip der Schmalenbach’schen dynamischen Bilanzierung, welches besagt, dass die Summe der Abschnittserfolge deckungsgleich mit dem Totalerfolg sein muss.

Zweitens muss der als Differenz zwischen Erträgen und Aufwendungen ermittelte Periodengewinn G_t um kalkulatorische Zinsen der Kapitalbindung der Vorperiode KB_{t − 1} korrigiert werden:

$\sum_{s=0}^{t-1} G_s = KB_{t-1}+\sum_{s=0}^{t-1}Z_s$

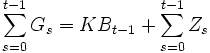
mit KB₀ = KB_T = 0

• KB_t Kapitalbestand zum Zeitpunkt t
• KB_{t − 1} Kapitalbestand der Vorperiode
• s jeweilige Periode, die bis zum Zeitpunkt t − 1 abgelaufen ist.

Beweis

Die Kapitalbindung, also die Differenz der bis zum Zeitpunkt t kumulierten Gewinne und der kumulierten Zahlungsüberschüsse, wird zu Beginn jeder Periode wie folgt ermittelt:

$KB_{t-1}=\sum_{s=0}^{t-1} G_s - \sum_{s=0}^{t-1}(EZ_s - AZ_s)$

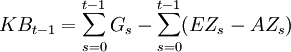
• i Kapitalkostensatz

Wenn beide o.g. Prämissen erfüllt sind, ergibt sich für den Kapitalwert zum Entscheidungszeitpunkt folgende Gleichung:

$K_0 = \sum_{t=0}^T \frac {EZ_t - AZ_t}{(1+i)^t} = \sum_{t=0}^T \frac {G_t - i \cdot KB_{t-1}}{(1+i)^t} = \sum_{t=0}^T \frac {G_t^*}{(1+i)^t}$

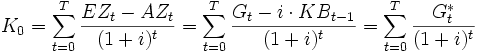
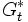• $G_t^*$ Residualgewinn zum Zeitpunk t

Beispiel

Für folgende Beispiele wird als Zinssatz 10% angenommen.

Tabelle 1: Investitionsrechnung auf Basis von Zahlungen bei einem Investitionsbetrag von 1000

Jahr	0	1	2	3	4	5
Investitionsauszahlung	-1000
Einzahlungen		1000	1000	1000	1000	1000
Auszahlungen		600	600	600	600	600
Cash-Flow	-1000	400	400	400	400	400
Abzinsfaktoren		0,909	0,826	0,751	0,683	0,621
Barwert		364	331	301	273	248
Kapitalwert	516

Tabelle 2: Kapitalwertberechnung auf Basis von Kosten nach dem Preinreich-Lücke-Theorem

Jahr	0	1	2	3	4	5
Erlöse		1000	1000	1000	1000	1000
Kosten		600	600	600	600	600
Abschreibungen		200	200	200	200	200
Operatives Ergebnis (vor kalk. Zinsen)		200	200	200	200	200
kalk. Zinsen (auf Basis Vermögen)		100	80	60	40	20
Residuales Ergebnis (BE nach kalk. Zinsen)		100	120	140	160	180
Abzinsfaktoren		0,909	0,826	0,751	0,683	0,621
Barwert		91	99	105	109	112
Kapitalwert	516

Tabelle 3: Kapitalwertberechnung auf Basis von Kosten nach dem Preinreich-Lücke-Theorem mit modifizierter Abschreibungsmethode

Jahr	0	1	2	3	4	5
Erlöse		1000	1000	1000	1000	1000
Kosten		600	600	600	600	600
Abschreibungen		400	275	175	100	50
Operatives Ergebnis		0	125	225	300	350
kalk. Zinsen		100	60	32,5	15	5
Residuales Ergebnis		-100	65	192,5	285	345
Abzinsfaktoren		0,909	0,826	0,751	0,683	0,621
Barwert		-91	54	145	195	214
Kapitalwert	516

Aus Tabelle 3 wird deutlich, dass unter den Bedingungen des Preinreich-Lücke-Theorems, bei einer periodenerfolgbasierten Kapitalwertrechnung eine Änderung der Abschreibungsmethode keinen Einfluss auf die Kapitalwertberechnung hat. Die verwendete Tabellenform ist die Basis für die Methode des vollständigen Finanzplans, welche eine einfache Nachvollziehung des Lücke-Theorems erlaubt.

Literatur

• Wolfgang Lücke: „Investitionsrechnung auf der Basis von Ausgaben oder Kosten?“ in Zeitschrift für handelswissenschaftliche Forschung, 1955, S. 310-324

Weblinks

• http://hans-markus.de/finance/86/hauptstudium_drei/luecke_theorem/