Apollonisches Problem

Beispiel von drei Kreisen (schwarz) und den zugehörigen acht Lösungskreisen

Apollonios von Perge widmet dem geometrischen Problem, einen Kreis zu konstruieren, der drei beliebige andere Kreise berührt, ein nicht erhaltenes Buch ("Über Berührungen").

Da man bei den Ausgangskreisen auch von einem unendlich kleinen Radius und einem unendlich großen Radius ausgehen kann, kann nicht nur von drei Kreisen, sondern auch von Punkten und Geraden (Tangenten) ausgegangen werden. Insgesamt gibt es zehn Kombinationsmöglichkeiten für die gegebenen Stücke, die weiter unten aufgeführt sind.

Da die vollständige Lösung der Probleme alle Konstruktionsfälle mit Berührungen (Tangenten) von Kreisen, Punkten und Geraden löst, sind natürlich auch die Berührkreise am Dreieck enthalten (Ankreis, Inkreis, Umkreis).

Geschichtliches

Die zwei einfachsten Fälle (drei Punkte und drei Geraden) wurden bereits von Euklid gelöst, die anderen waren im verlorenen Werk des Apollonius enthalten. Der Satz von Descartes befasst sich mit dem Fall dreier Kreise, die sich paarweise berühren. François Viète löste das Problem als erster in moderner Zeit mittels eines nichtlinearen Systems dreier quadratischer Gleichungen. Eine sehr elegante Lösung stammt von Joseph Gergonne.

Lösungsmethoden

Schnitt von Hyperbeln

Die Lösungsmethode von Adrian van Roomen (1596) basiert auf dem Schnitt von Hyperbeln, stellt aber keine Konstruktion mit Zirkel und Lineal dar. Die Mittelpunkte der gegebenen Kreise seien mit M₁, M₂, M₃ bezeichnet, ihre Radien mit r₁, r₂, r₃. Gesucht sei ein Kreis mit Mittelpunkt M_s und Radius r_s. Dann muss für i = 1,2,3 der Abstand $\overline{M_s M_i}$ jeweils gleich r_i + r_s oder gleich | r_i − r_s | sein - je nachdem, ob die Berührung ausschließend oder einschließend ist. Die Differenz der Abstände zwischen M_s und zwei gegebenen Kreismittelpunkten muss also jeweils einen bestimmten Wert haben, der nur von den gegebenen Radien abhängt. Anders ausgedrückt: Der gesuchte Kreismittelpunkt muss auf einer bestimmten Hyperbel liegen, deren Brennpunkte mit den gegebenen Mittelpunkten übereinstimmen. Durch Schnitt von zwei Hyperbeln dieser Art findet man den Mittelpunkt des gesuchten Kreises.

Algebraische Lösung

Die Bedingungen für die Abstände des gesuchten Kreismittelpunkts von den gegebenen Mittelpunkten führen auf ein Gleichungssystem des folgenden Typs für die drei Unbekannten x_s, y_s und r_s:

$\left( x_s - x_1 \right)^2 + \left( y_s - y_1 \right)^2 = \left( r_s \pm r_1 \right)^2$

$\left( x_s - x_2 \right)^2 + \left( y_s - y_2 \right)^2 = \left( r_s \pm r_2 \right)^2$

$\left( x_s - x_3 \right)^2 + \left( y_s - y_3 \right)^2 = \left( r_s \pm r_3 \right)^2$

Bei ausschließender Berührung gilt das Pluszeichen von $\pm$, bei einschließender Berührung das Minuszeichen. Subtrahiert man beispielsweise die zweite Gleichung von der ersten und die dritte von der zweiten, so kann man x_s und y_s durch r_s ausdrücken, indem man ein lineares Gleichungssystem mit zwei Unbekannten löst. Durch Einsetzen des Ergebnisses in eine der gegebenen Gleichungen erhält man eine quadratische Gleichung, mit der sich r_s bestimmen lässt.

Spezialfälle

Überblick

Table 1: Die zehn Typen des Apollonios-Problems

Nummer	Code	Gegeben	Zahl der Lösungen (im Allgemeinen)	Beispiel (gegebene Elemente schwarz; Lösung pink)
1	PPP	drei Punkte	1
2	LPP	eine Gerade, zwei Punkte	2
3	LLP	zwei Geraden, ein Punkt	2
4	CPP	ein Kreis, zwei Punkte	2
5	LLL	drei Geraden	4
6	CLP	ein Kreis, eine Gerade, ein Punkt	4
7	CCP	zwei Kreise, ein Punkt	4
8	CLL	ein Kreis, zwei Geraden	8
9	CCL	zwei Kreise, eine Gerade	8
10	CCC	drei Kreise (das klassische Problem)	8

Für die vier einfachsten Fälle können mit relativ einfachen Möglichkeiten Lösungen für die Kreisradien angegeben werden:

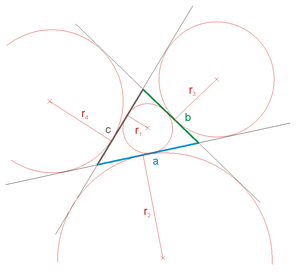
Drei Geraden

Für drei sich schneidende Geraden gibt es vier Lösungen

Für drei sich schneidende Geraden (nicht parallel oder übereinander liegend) gibt es vier Lösungen. Sind zwei der Geraden parallel, gibt es nur zwei Lösungen, für drei Parallelen gibt es keine Lösung und für parallele Geraden mit Abstand 0 gibt es unendlich viele Lösungen.

Die drei Geraden bilden mit ihren Schnittpunkten ein Dreieck mit den Seiten a,b,c. Deshalb kommen hier die Regeln für den Inkreis und die Ankreise zur Anwendung:

$r = \frac{2 A}{a+b+c} = \frac As = \frac{a}{\cot\frac\beta2+\cot\frac\gamma2}$

mit den Innenwinkeln α,β,γ, dem Flächeninhalt A und dem halben Umfang s:

$s=\frac{a+b+c}{2}$

Um einen Ausdruck zu erhalten, der nur die Seitenlängen verwendet, kann der Satz des Heron benutzt werden:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

Die entsprechenden Formeln für die Ankreise lauten

$r_a = \frac{2 A}{b+c-a} = \frac A{s-a} = \frac a{\tan\frac\beta2+\tan\frac\gamma2}$

bzw. für die anderen Ankreisen entsprechend.

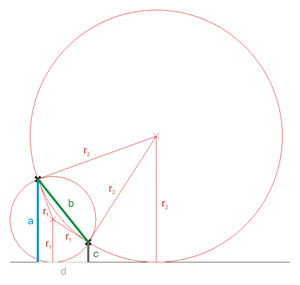
Zwei Geraden, ein Punkt

Für zwei sich schneidende Geraden und einen Punkt gibt es im Allgemeinen zwei Lösungen

Es gibt verschiedene Fälle:

• Die Geraden sind parallel: Falls der Punkt außerhalb des von den Geraden begrenzten Bereiches liegt, gibt es keine Lösungen. Liegt er auf einer der Geraden, gibt es eine Lösung. Liegt er dazwischen, zwei Lösungen; der Kreisdurchmesser ist jeweils gleich dem Abstand der Geraden.
• Die Geraden sind nicht parallel:
  • Ist der Punkt der Schnittpunkt der Geraden, gibt es keine Lösung.
  • Liegt der Punkt P auf einer der Geraden, g, ist jedoch nicht der Schnittpunkt, gibt es zwei Lösungen; die Mittelpunkte der Kreise sind die Schnittpunkte der beiden Winkelhalbierenden mit der Senkrechten zu g durch P.
  • Liegt der Punkt auf keiner der Geraden, gibt es zwei Lösungen; dies ist der generische Fall. Es seien P' das Bild von P unter der Spiegelung an der zugehörigen Winkelhalbierenden w und S der Schnittpunkt der Senkrechten zu w durch P und P' mit einer der Geraden, g. Dann haben die Berührpunkte der beiden Kreise mit g den Abstand $\sqrt{\overline{SP}\cdot\overline{SP'}}$ von S. Ihre Mittelpunkte sind die jeweiligen Schnittpunkte der Senkrechten zu g durch die so ermittelten Berührpunkte mit w.

Eine Gerade, zwei Punkte

Für eine Gerade und zwei Punkte gibt es i. a. zwei Lösungen

Für zwei Punkte und eine Gerade gibt es zwei Lösungen, bei den unten genannten Spezialfällen nur eine und für zwei auf der Geraden liegende Punkte unendlich viele Lösungen.

Dieser Fall ist im Wesentlichen äquivalent zum vorherigen; die Mittelsenkrechte der Verbindungsstrecke der beiden Punkte entspricht dabei der Winkelhalbierenden. Umgekehrt liegt beim vorherigen Problem auch der an der Winkelhalbierenden gespiegelte Punkt auf den gesuchten Kreisen.

Die vorgegebenen Punkte seien mit P₁ und P₂ bezeichnet, die vorgegebene Gerade mit g. Weiter sei S der Schnittpunkt der Geraden (P₁P₂) mit g und $\alpha<90^\circ$ der Schnittwinkel. Dann haben die Berührpunkte der beiden gesuchten Kreise nach dem Sekantentangentensatz den Abstand $t=\sqrt{\overline{SP_1}\cdot\overline{SP_2}}$ von S. Die Mittelpunkte können dann als Schnittpunkte der Mittelsenkrechten von P₁P₂ mit den Senkrechten zu g in den Berührpunkten ermittelt werden.

Drei Punkte

Für drei Punkte gibt es i. a. eine Lösung

Für drei Punkte gibt es eine Lösung. Wenn mindestens zwei Punkte aufeinander liegen, gibt es unendlich viele Lösungen.

Die drei Punkte bilden ein Dreieck mit den Seiten a, b, c. Der gesuchte Kreis ist der Umkreis dieses Dreiecks:

$r = \frac{abc}{4A} = \frac{ab}{2h_c} = \frac a{2\sin\alpha}$

Für die Bestimmung des Flächeninhaltes A kann wieder der Satz des Heron verwendet werden.

Das Problem ist in allen Fällen mit den klassischen Mitteln (Zirkel und Lineal) lösbar. Falls zwei der Kreise mindestens einen Punkt M gemein haben, kann man das Problem vereinfachen, indem man es durch eine Spiegelung an einem Kreis mit Mittelpunkt M auf den Fall zurückführt, dass zwei der Kreise in Geraden ausarten.

Weblinks

• Beschreibung des Problems und Lösung des Drei-Kreise-Problems mit quadratischen Gleichungen
• Lösungen mit quadratischen Gleichungen
• Berechnung aller Varianten mittels eines Mathematikprogramms