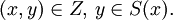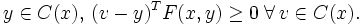Mathematical Programs with Equilibrium Constraints
- Mathematical Programs with Equilibrium Constraints
-
MPECs (Mathematical Programs with Equilibrium Constraints), zu deutsch etwa 'Mathematische Optimierungsprobleme mit Gleichgewichtsnebenbedingungen', stellen eine spezielle Problemklasse der mathematischen Optimierung dar. MPECs sind eng verwandt mit Optimalsteuerungsproblemen und zeichnen sich dadurch aus, dass die essentiellen Nebenbedingungen in Form einer Variationsungleichung oder eines äquivalenten Komplementaritätssystems formuliert sind. Zahlreiche Anwendungen finden sich in der Ingenieurswelt oder in der Wirtschaft, wie etwa in der Robotik, in der Spieltheorie oder in der Berechnung von Optionen.
Problemformulierung
In der Problemklasse der MPECs hängt die zu minimierende Zielfunktion f von zwei Variablen 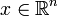 und
und 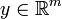 ab. Weiters sei
ab. Weiters sei 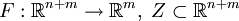 nichtleer und abgeschlossen und
nichtleer und abgeschlossen und 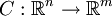 eine mengenwertige Funktion mit konvexen Funktionswerten. Das MPEC in seiner allgemeinsten Form ist definiert durch:
eine mengenwertige Funktion mit konvexen Funktionswerten. Das MPEC in seiner allgemeinsten Form ist definiert durch:
Minimiere f(x,y), unter der Nebenbedingung
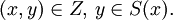
Dabei ist S(x) die Lösungsmenge der Variationsungleichung:
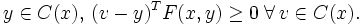
Besonderheiten
Einige Besonderheiten der Problemklasse der MPECs sind:
Literatur
- Z.-Q. Luo, J.-S. Pang und D. Ralph: Mathematical Programs with Equilibrium Constraints. Cambridge University Press, 1996, ISBN 0-521-57290-8.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Mathematical programming with equilibrium constraints — (MPEC) is the study of constrained optimization problems where the constraints include variational inequalities or complementarities. MPEC is related to the Stackelberg game. MPEC is used in the study of engineering design, economic equilibrium… … Wikipedia
Mathematical optimization — For other uses, see Optimization (disambiguation). The maximum of a paraboloid (red dot) In mathematics, computational science, or management science, mathematical optimization (alternatively, optimization or mathematical programming) refers to… … Wikipedia
Mathematical economics — Economics … Wikipedia
Algebraic modeling language — Algebraic Modeling Languages (AML) are high level programming languages for describing and solving high complexity problems for large scale mathematical computation (i.e. large scale optimization type problems). One particular advantage of AMLs… … Wikipedia
MPEC — MPECs (Mathematical Programs with Equilibrium Constraints), zu deutsch etwa Mathematische Optimierungsprobleme mit Gleichgewichtsnebenbedingungen , stellen eine spezielle Problemklasse der mathematischen Optimierung dar. MPECs sind eng verwandt… … Deutsch Wikipedia
Optimization (mathematics) — In mathematics, the term optimization, or mathematical programming, refers to the study of problems in which one seeks to minimize or maximize a real function by systematically choosing the values of real or integer variables from within an… … Wikipedia
Chemical equilibrium — In a chemical reaction, chemical equilibrium is the state in which the concentrations of the reactants and products have not yet changed with time. It occurs only in reversible reactions, and not in irreversible reactions. Usually, this state… … Wikipedia
IPOPT — IPOPT, short for Interior Point OPTimizer, pronounced I P Opt , is a software library for large scale nonlinear optimization of continuous systems. It is written in Fortran and C and is released under the CPL. IPOPT implements a primal dual… … Wikipedia
education — /ej oo kay sheuhn/, n. 1. the act or process of imparting or acquiring general knowledge, developing the powers of reasoning and judgment, and generally of preparing oneself or others intellectually for mature life. 2. the act or process of… … Universalium
Stable model semantics — The concept of a stable model, or answer set, is used to define a declarative semantics for logic programs with negation as failure. This is one of several standard approaches to the meaning of negation in logic programming, along with program… … Wikipedia
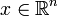 und
und 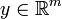 ab. Weiters sei
ab. Weiters sei 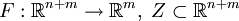 nichtleer und abgeschlossen und
nichtleer und abgeschlossen und 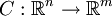 eine mengenwertige Funktion mit konvexen Funktionswerten. Das MPEC in seiner allgemeinsten Form ist definiert durch:
eine mengenwertige Funktion mit konvexen Funktionswerten. Das MPEC in seiner allgemeinsten Form ist definiert durch: