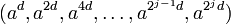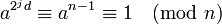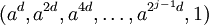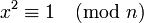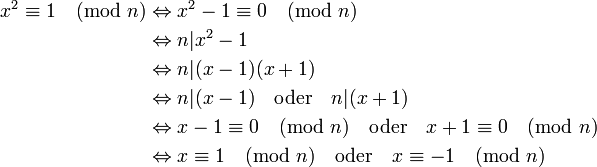Miller-Rabin-Algorithmus

Der Miller-Rabin-Test oder Miller-Selfridge-Rabin-Test ist ein Algorithmus aus dem mathematischen Teilgebiet Zahlentheorie, insbesondere der algorithmischen Zahlentheorie. Er ist ein probabilistischer Primzahltest. Erhält er eine natürliche Zahl n als Eingabe, so gibt er entweder „n ist keine Primzahl“ oder „n ist wahrscheinlich eine Primzahl“ aus. Da der Miller-Rabin-Test nicht sicher feststellt, ob eine Zahl eine Primzahl ist, zählt er zur Klasse der Monte-Carlo-Algorithmen. Zahlen, bei denen der Miller-Rabin-Test immer „n ist wahrscheinlich eine Primzahl“ ausgibt, obwohl sie keine Primzahlen sind, nennt man starke Pseudoprimzahlen.

Der Miller-Rabin-Test ist nach Gary Miller und Michael O. Rabin benannt. John L. Selfridge hat diesen Test schon 1974 verwendet, bevor Miller ihn veröffentlicht hatte. Daher rührt der alternative Name Miller-Selfridge-Rabin-Test. ^[1]

Der Miller-Rabin-Test funktioniert ähnlich wie der Solovay-Strassen-Test, ist diesem allerdings in allen Aspekten überlegen. Er ist schneller, seine Irrtumswahrscheinlichkeit ist geringer und jede Zahl, die der Solovay-Strassen-Test als zusammengesetzt erkennt, weist auch der Miller-Rabin-Test als nicht-prim aus.

Algorithmus

Es sei n eine ungerade Zahl, von der festgestellt werden soll, ob sie eine Primzahl ist oder nicht. Zuerst wählt man eine Basis a zufällig aus den Zahlen 2, 3, …, n − 1.

Der nächste Schritt benutzt einen Test, den nur Primzahlen und starke Pseudoprimzahlen bestehen können. Hierzu wird n − 1 eindeutig in seinen ungeraden und geraden Anteil faktorisiert: $n - 1 = d \cdot 2^j$.

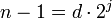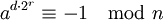Wenn $a^d \equiv 1 \mod n$ ist oder $a^{d \cdot 2^r} \equiv -1 \mod n$ für ein r mit 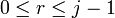$0 \le r \le j-1$ gilt, dann ist n entweder eine Primzahl oder eine starke Pseudoprimzahl.

Funktionsweise

Der Miller-Rabin-Test berechnet modulo n die Folge

$(a^d, a^{2d}, a^{4d}, \ldots, a^{2^{j-1}d}, a^{2^jd})$

mit 2^jd = n − 1. Jedes Element der Folge ist hierbei das Quadrat seines Vorgängers.

Ist n eine Primzahl, dann gilt nach dem kleinen fermatscher Satz

$a^{2^jd} \equiv a^{n-1} \equiv 1 \pmod n$

und die vom Miller-Rabin-Test berechnete Folge hat deshalb die Form

$(a^d, a^{2d}, a^{4d}, \ldots, a^{2^{j-1}d}, 1)$

Die einzigen Zahlen x mit

$x^2 \equiv 1 \pmod n$

sind für eine Primzahl n die Zahlen 1 und -1, wie der folgenden Beweis zeigt.

$\begin{align} x^2 \equiv 1 \pmod n &\Leftrightarrow x^2 - 1 \equiv 0 \pmod n\\ &\Leftrightarrow n | x^2 - 1\\ &\Leftrightarrow n | (x - 1)(x + 1)\\ &\Leftrightarrow n | (x - 1) \quad \text{oder} \quad n|(x + 1)\\ &\Leftrightarrow x - 1 \equiv 0 \pmod n \quad \text{oder} \quad x + 1 \equiv 0 \pmod n\\ &\Leftrightarrow x \equiv 1 \pmod n \quad \text{oder} \quad x \equiv -1 \pmod n\\ \end{align}$

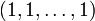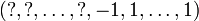Aus diesem Grund ist der Vorgänger einer 1 in der Folge immer eine 1 oder eine -1. Dies führt dazu, dass für eine Primzahl n die Folge des Miller-Rabin-Tests entweder $(1, 1, \ldots, 1)$ oder $(?, ?, \ldots, ?, -1, 1, \ldots, 1)$ ist, wobei die Fragezeichen für beliebige Zahlen stehen.

Ist n eine beliebige Zahl und beginnt die vom Miller-Rabin-Test berechnete Folge nicht mit 1 und enthält auch keine -1, dann kann n keine Primzahl sein. Es gibt allerdings zusammengesetzte Zahlen, bei denen die Folge bei bestimmten Basen mit 1 beginnt oder eine -1 enthält. Das sind die starken Pseudoprimzahlen.

Zuverlässigkeit

Ist 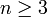$n\geq 3$ ungerade und nicht prim, so enthält die Menge 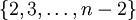$\{2,3,\dots,n-2\}$ höchstens 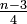$\tfrac{n-3}{4}$ Elemente a mit ggT(a,n) = 1, die keine Zeugen für die Zusammengesetztheit von n sind. (Ist ggT(a,n) > 1, oder 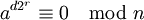$a^{d 2^r} \equiv 0 \mod n$ für irgendein r < s, dann wird n natürlich sofort als nicht-prim erkannt). Damit ist die Wahrscheinlichkeit, dass n zusammengesetzt ist und ein zufälliges a dafür kein Zeuge ist, kleiner als $\tfrac{1}{4}$.

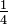Wiederholt man den Test mehrfach für verschiedene a aus [2,n-2] sinkt die Wahrscheinlichkeit weiter ab. So erreicht man beispielsweise schon nach vier Schritten, dass die Fehlklassierung einer zusammengesetzten Zahl (also die Ausgabe, dass a wahrscheinlich prim sei, obwohl es zusammengesetzt ist) nur noch mit einer Wahrscheinlichkeit von weniger als 0,4% geschieht.

Einzelnachweise

1. ↑ Song Y. Yan: Number theory for computing. 2. Auflage. Springer, 2002, ISBN 3-540-43072-5, S. 208-214

Literatur

• Johannes Buchmann: Einführung in die Kryptographie. 2. Auflage. Springer, 2001, ISBN 3-540-41283-2, S. 108–111

Weblinks

• Anschauliche Darstellung des Miller-Rabin Primzahltest