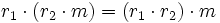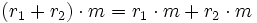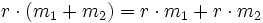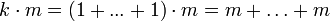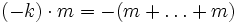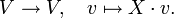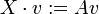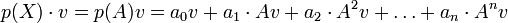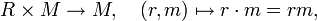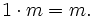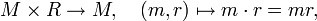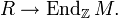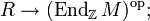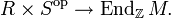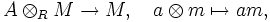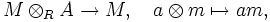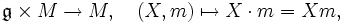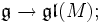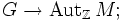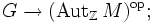Moduln

Links- oder Rechts-Modul

berührt die Spezialgebiete

Mathematik Abstrakte Algebra Lineare Algebra

ist Spezialfall von

additive Abelsche Gruppe trägt Operation eines Rings

umfasst als Spezialfälle

Ring (Modul über sich selbst) kommutativer Modul Vektorraum

Ein Modul (maskulinum, auf der ersten Silbe betont; Plural: Moduln) ist eine algebraische Struktur, die eine Verallgemeinerung eines Vektorraums darstellt.

Moduln über einem kommutativen Ring mit Einselement

In diesem einfachsten Fall kann man direkt die Axiome eines Vektorraums abschreiben und überall „Körper“ durch „Ring“ ersetzen: Ein Modul über einem kommutativen Ring 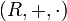$(R, +, \cdot)$ mit Einselement ist eine abelsche Gruppe (M, + ) zusammen mit einer Abbildung

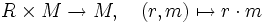$R\times M\to M,\quad(r,m)\mapsto r\cdot m$ („Skalarmultiplikation“),

so dass gilt:

$r_1\cdot(r_2\cdot m) = (r_1\cdot r_2)\cdot m$

$(r_1+r_2)\cdot m=r_1\cdot m+r_2\cdot m$

$r\cdot (m_1+m_2)=r\cdot m_1+r\cdot m_2$

Fordert man zusätzlich noch 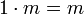$1\cdot m=m$, so nennt man den Modul unitär.

Das Studium dieser Moduln ist Gegenstand der kommutativen Algebra.

Beispiele

Abelsche Gruppen

Jede abelsche Gruppe ist auf eindeutige Weise ein unitärer $\mathbb{Z}$-Modul: Wegen

$1\cdot m=m$

sind höchstens

$k\cdot m=(1+...+1) \cdot m=m+\ldots+m$

und analog

$(-k)\cdot m=-(m+\ldots+m)$

(für natürliche Zahlen k) denkbar - da diese einzig mögliche Verknüpfung aber die Modulaxiome erfüllt, folgt die Behauptung. (Hier wurde die abelsche Gruppe additiv geschrieben).

Vektorräume mit einer linearen Abbildung in sich selbst

Sei k[X] der Polynomring über einem Körper k. Dann entsprechen die k[X]-Moduln eins-zu-eins den Paaren (V,A) bestehend aus einem k-Vektorraum V und einem Endomorphismus A von V:

• Sei M ein k[X]-Modul. Wir stellen fest, dass M auch ein k-Vektorraum ist, da k in k[X] eingebettet ist. Sei V dieser Vektorraum. Das zu M gehörige Paar ist nun (V,A), wobei dem A durch

$V\to V,\quad v\mapsto X\cdot v.$

gegeben ist.

• Zu einem Paar (V,A) definieren wir eine k[X]-Modulstruktur durch

$X \cdot v := Av$

und setzen das k-linear auf k[X] fort, d.h.:

$p(X)\cdot v=p(A) v=a_0 v + a_1\cdot Av + a_2\cdot A^2v + \ldots + a_n\cdot A^nv$

für $p(X)=a_0+a_1X+a_2X^2+\ldots+a_nX^n\in k[X].$

Ringideale

Jeder Ring ist ein Modul über sich selbst mit der Ringmultiplikation als Operation. Die Untermoduln entsprechen dann genau den Idealen von R (da R in diesem Abschnitt kommutativ ist, brauchen wir nicht zwischen Links- und Rechtsidealen zu unterscheiden).

Moduln über einem beliebigen Ring

Es sei R ein Ring. Ist R nicht kommutativ, so muss man zwischen Links- und Rechtsmoduln unterscheiden.

Ein R-Linksmodul ist eine abelsche Gruppe M zusammen mit einer $\mathbb{Z}$-bilinearen Abbildung

$R\times M\to M,\quad (r,m)\mapsto r\cdot m = rm,$

d.h.

(r₁ + r₂)m = r₁m + r₂m und r(m₁ + m₂) = rm₁ + rm₂,

so dass

r₁(r₂m) = (r₁r₂)m für alle $r_1,r_2\in R,m\in M$

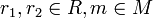
gilt. Wird R als unitär angenommen, so fordert man meist auch, dass M ein unitärer Modul ist, d.h.

$1\cdot m=m.$

Ein R-Rechtsmodul ist eine abelsche Gruppe M zusammen mit einer $\mathbb{Z}$-bilinearen Abbildung

$M\times R\to M,\quad (m,r)\mapsto m\cdot r=mr,$

so dass

(mr₁)r₂ = m(r₁r₂) für alle $r_1,r_2\in R,m\in M.$

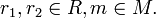
Unitäre Rechtsmoduln sind analog zu unitären Linksmoduln definiert.

Ist R kommutativ, so stimmen die Begriffe Links- und Rechtsmodul (bis auf die Schreibweise) überein, und man spricht einfach von R-Moduln.

Alternative Definitionen

• Ein R-Linksmodul ist eine abelsche Gruppe M zusammen mit einem (ggf. unitären) Ringhomomorphismus

$R\to\mathrm{End}_{\mathbb Z}\,M.$

Dabei ist 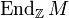$\mathrm{End}_{\mathbb Z}\,M$ der Ring der Endomorphismen von M mit der Verknüpfung als Produkt:

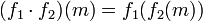$(f_1\cdot f_2)(m) = f_1(f_2(m))$ für $f_1,f_2\in\mathrm{End}_{\mathbb Z}\,M, m\in M.$

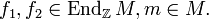
• Ein R-Rechtsmodul ist eine abelsche Gruppe M zusammen mit einem (ggf. unitären) Ringhomomorphismus

$R\to(\mathrm{End}_{\mathbb Z}\,M)^{\mathrm{op}};$

Dabei sei 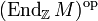$(\mathrm{End}_{\mathbb Z}\,M)^\mathrm{op}$ der Ring der Endomorphismen von M mit der Rechtsverknüpfung als Produkt:

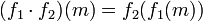$(f_1\cdot f_2)(m) = f_2(f_1(m))$ für $f_1,f_2\in(\mathrm{End}_{\mathbb Z}\,M)^{\mathrm{op}}, m\in M.$

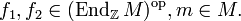
Bimoduln

Es seien R und S Ringe. Dann ist ein R-S-Bimodul eine abelsche Gruppe M zusammen mit einer R-Linksmodul- und einer S-Rechtsmodulstruktur, so dass

(rm)s = r(ms) für $r\in R,s\in S,m\in M$

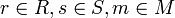
gilt.

Alternativ ist ein R-S-Bimodul eine abelsche Gruppe M zusammen mit einem Ringhomomorphismus

$R\times S^{\mathrm{op}}\to\mathrm{End}_{\mathbb Z}\,M.$

Moduln über einer assoziativen Algebra

Ist R ein kommutativer Ring und A eine assoziative R-Algebra, so ist ein A-Linksmodul ein R-Modul M zusammen mit einem R-Modulhomomorphismus

$A\otimes_RM\to M,\quad a\otimes m\mapsto am,$

so dass

a₁(a₂m) = (a₁a₂)m für $a_1,a_2\in A,m\in M$

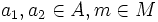
gilt.

Ein A-Rechtsmodul ist ein R-Modul M zusammen mit einem R-Modulhomomorphismus

$M\otimes_RA\to M,\quad a\otimes m\mapsto am,$

so dass

(ma₁)a₂ = m(a₁a₂) für $a_1,a_2\in A,m\in M$

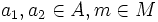
gilt.

Unitäre Moduln und Bimoduln sind analog zum Fall der Ringe definiert.

Moduln über einer Liealgebra

Es sei $\mathfrak g$ eine Liealgebra über einem Körper k. Ein $\mathfrak g$-Modul oder eine Darstellung von $\mathfrak g$ ist ein k-Vektorraum M zusammen mit einer k-bilinearen Abbildung

$\mathfrak g\times M\to M,\quad (X,m)\mapsto X\cdot m = Xm,$

so dass

[X,Y]m = XYm − YXm für $X,Y\in\mathfrak g,m\in M$

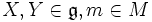
gilt.

Alternativ ist ein $\mathfrak g$-Modul ein k-Vektorraum M zusammen mit einem Homomorphismus von Liealgebren über k

$\mathfrak g\to\mathfrak{gl}(M);$

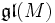dabei ist $\mathfrak{gl}(M)$ die k-Algebra der Endomorphismen von M mit dem Kommutator als Lieklammer.

$\mathfrak g$-Moduln sind dasselbe wie Moduln unter der universellen einhüllenden Algebra von $\mathfrak g$.

Moduln über einer Gruppe

Es sei 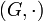$(G,\cdot)$ eine Gruppe. Ein G-Linksmodul ist eine abelsche Gruppe (M, + ) zusammen mit einer Abbildung

$G\times M\to M, (g,m)\mapsto gm:=g\cdot m$,

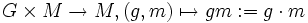so dass

g(m₁ + m₂) = gm₁ + gm₂ für $g\in G,m_1,m_2\in M$

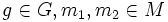
und

(g₁g₂)m = g₁(g₂m) für $g_1,g_2\in G,m\in M$

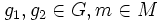
gilt.

Ein G-Rechtsmodul ist analog definiert; die zweite Bedingung ist durch

m(g₁g₂) = (mg₁)g₂ für $g_1,g_2\in G,m\in M$

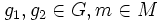
zu ersetzen.

Alternativ dazu ist ein G-Linksmodul eine abelsche Gruppe (M, + ) zusammen mit einem Gruppenhomomorphismus

$G\to\mathrm{Aut}_{\mathbb Z}\,M;$

dabei ist 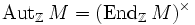$\mathrm{Aut}_{\mathbb Z}\,M = (\mathrm{End}_{ \mathbb Z}\,M )^\times$ die Gruppe der Automorphismen von M mit der Verknüpfung

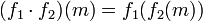$(f_1\cdot f_2)(m)=f_1(f_2(m))$ für $f_1,f_2\in\mathrm{Aut}_{\mathbb Z}\,M,m\in M.$

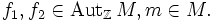
Ein G-Rechtsmodul ist eine abelsche Gruppe (M, + ) zusammen mit einem Gruppenhomomorphismus

$G\to(\mathrm{Aut}_{\mathbb Z}\,M)^{\mathrm{op}};$

das Produkt auf 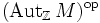$(\mathrm{Aut}_{\mathbb Z}\,M)^{\mathrm{op}}$ ist durch

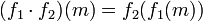$(f_1\cdot f_2)(m)=f_2(f_1(m))$ für $f_1,f_2\in(\mathrm{Aut}_{\mathbb Z}\,M)^{\mathrm{op}},m\in M$

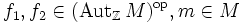
gegeben.

Ist R weiter ein Ring, so ist ein G-R-Modul eine abelsche Gruppe mit einer R-Modul- und einer G-Modulstruktur, die in dem folgenden Sinne kompatibel sind:

r(gm) = g(rm) für $r\in R,g\in G,m\in M.$

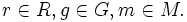
Alternativ ist ein G-R-Modul ein R-Modul zusammen mit einem Gruppenhomomorphismus

$G\to\mathrm{Aut}_R\,M;$

dabei ist Aut_R M die Gruppe der Automorphismen von M als R-Modul.

G-R-Moduln sind dasselbe wie Moduln über dem Gruppenring R[G].

Ist k speziell ein Körper, so stimmt der Begriff des G-k-Moduls mit dem der k-linearen Darstellung von G überein.

Siehe auch

• Einfacher Modul
• Vektorraum
• Moduln über Hauptidealringen

Weblinks

http://www.mathematik-netz.de/pdf/Moduln.pdf Alexander Hölzle: Einführung in die Modultheorie.