Körpertheorie

Körper

berührt die Spezialgebiete

Mathematik Abstrakte Algebra Gruppentheorie Zahlentheorie Lineare Algebra Analysis

ist Spezialfall von

additive Abelsche Gruppe kommutativer Ring Schiefkörper Vektorraum

umfasst als Spezialfälle

endlicher Körper p-adische Zahlen Funktionenkörper rationale Zahlen reelle Zahlen komplexe Zahlen

Ein Körper ist im mathematischen Teilgebiet der Algebra eine ausgezeichnete algebraische Struktur, in der die Addition, Subtraktion, Multiplikation und Division wie bei den „normalen“ (reellen) Zahlen durchgeführt werden können.

Die Bezeichnung Körper wurde im 19. Jahrhundert von Richard Dedekind eingeführt. Bourbaki verwendet die Begriffe anders: er bezeichnet Schiefkörper als Körper und die hier besprochenen Körper als kommutative Körper.

Formale Definition

Ein kommutativer unitärer Ring, der nicht der Nullring ist, heißt ein Körper, wenn in ihm jedes von Null verschiedene Element multiplikativ invertierbar ist.

Anders formuliert, ist ein Körper ein kommutativer unitärer Ring K, in dem die Einheitengruppe K ^* gleich 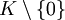$K\setminus\{0\}$, also maximal groß, ist.

Hier eine Einzelaufzählung der benötigten Axiome:

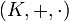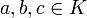Ein Tripel $(K,+,\cdot)$, bestehend aus einer Menge K und zwei binären Verknüpfungen „ + “ und „$\cdot$“ (die üblicherweise Addition und Multiplikation genannt werden), ist genau dann ein Körper, wenn folgende Eigenschaften für alle $a, b, c\in K$ erfüllt sind:

1. Additive Eigenschaften:
   1. a + (b + c) = (a + b) + c (Assoziativität)
   2. a + b = b + a (Kommutativität)
   3. Es gibt ein Element 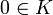$0\in K$ mit 0 + a = a (neutrales Element)
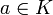   4. Zu jedem $a\in K$ existiert das additive Inverse − a mit ( − a) + a = 0
2. Multiplikative Eigenschaften:
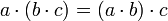   1. $a\cdot(b\cdot c) = (a\cdot b)\cdot c$ (Assoziativität)
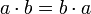   2. $a\cdot b = b\cdot a$ (Kommutativität)
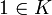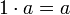   3. Es gibt ein Element $1\in K$ mit $1\cdot a=a$ (neutrales Element), und es ist $1\ne0$.
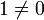   4. Zu jedem 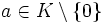$a\in K\setminus\{0\}$ existiert das multiplikative Inverse a ^{− 1} mit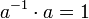 $a^{-1}\cdot a=1$
3. Zusammenspiel von additiver und multiplikativer Struktur:
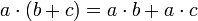   1. $a\cdot (b+c) = a\cdot b+a\cdot c$ (Links-Distributivität)

Das Rechts-Distributivgesetz 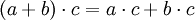$(a+b)\cdot c=a\cdot c+b\cdot c$ folgt dann aus den übrigen Eigenschaften.

Bemerkungen

Die Definition sorgt dafür, dass in einem Körper Addition, Subtraktion und Multiplikation in der „gewohnten“ Weise funktionieren (und die Division mit Ausnahme der verbotenen Division durch 0):

• Das Inverse von a bezüglich der Addition ist − a, und wird meist das Negative von a oder auch das „additiv Inverse“ zu a genannt.
• Das Inverse von a bezüglich der Multiplikation ist a ^{− 1} und wird das multiplikativ Inverse oder nur Inverse oder der Kehrwert von a genannt.
• Die 0 ist das einzige Element des Körpers, das keinen Kehrwert hat, die multiplikative Gruppe eines Körpers ist also $K^\times=K\setminus\{0\}$.

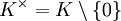Anmerkung: Die Bildung des Negativen eines Elementes hat nichts mit der Frage zu tun, ob das Element selbst negativ ist; beispielsweise ist das Negative der reellen Zahl − 2 die positive Zahl 2. In einem allgemeinen Körper gibt es keinen Begriff von negativen oder positiven Elementen. (Siehe auch geordneter Körper.)

Eigenschaften

Es gibt genau eine „0“ (Null-Element, neutrales Element bzgl. der Körper-Addition) und eine „1“ (Eins-Element, neutrales Element bzgl. der Körper-Multiplikation) in einem Körper.

Jeder Körper ist ein Ring. Die Eigenschaften der multiplikativen Gruppe heben den Körper aus den Ringen heraus. Wenn die Kommutativität der multiplikativen Gruppe nicht gefordert wird, erhält man den Begriff des Schiefkörpers.

Jeder Körper ist ein Vektorraum über sich selbst (das heißt mit sich selbst als zugrundeliegendem Skalarkörper).

Jeder Körper ist nullteilerfrei. Das heißt, dass ein Produkt zweier Elemente des Körpers genau dann 0 ist, wenn mindestens einer der beteiligten Faktoren 0 ist.

Beispiele

Bekannte Beispiele für Körper sind die Menge der rationalen Zahlen 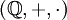$(\Bbb Q,+,\cdot)$, die Menge der reellen Zahlen 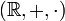$(\R,+,\cdot)$ und die Menge der komplexen Zahlen 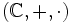$(\Bbb C,+,\cdot)$ jeweils mit der üblichen Addition und Multiplikation. Weitere Beispiele sind endliche Körper und die Körper der p-adischen Zahlen.

Kein Beispiel für einen Körper ist die Menge der ganzen Zahlen 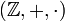$(\Bbb Z,+,\cdot)$: Zwar ist 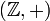$(\Bbb Z,+)$ eine Gruppe mit neutralem Element 0 und jedes 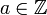$a\in\Bbb Z$ besitzt das additive Inverse − a, aber 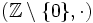$(\Bbb{Z}\setminus \{0\},\cdot)$ ist keine Gruppe. Immerhin ist 1 das neutrale Element, aber außer zu 1 und − 1 gibt es keine multiplikativen Inversen (zum Beispiel ist 3 ^{− 1} = 1 / 3 keine ganze, sondern eine echt rationale Zahl). Die ganzen Zahlen bilden lediglich einen Integritätsring, dessen Quotientenkörper die rationalen Zahlen sind.

Unterkörper

Ein Unter- bzw. Teilkörper ist eine Teilmenge eines Körpers, die mit den Operationen des Oberkörpers wieder einen Körper bildet. Dazu müssen folgende Aussagen für einen Unterkörper U eines Körpers K gelten:

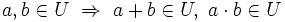• $a,b \in U\ \Rightarrow\ a + b \in U,\ a \cdot b \in U$ (Abgeschlossenheit bezüglich Addition und Multiplikation)
• $1_{K},\ 0_{K} \in U$ (Die neutralen Elemente von K sind in U.)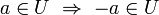
• $a \in U\ \Rightarrow\ -a \in U$ (Jedes additive Inverse von U ist in U.)
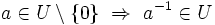• $a \in U \setminus \{0\}\ \Rightarrow\ a^{-1} \in U$ (Das multiplikativ Inverse zu jedem Element aus U mit Ausnahme der Null ist in U.)

Beispiel:

Der Körper der rationalen Zahlen $\mathbb{Q}$ ist ein Unterkörper der reellen Zahlen $\R$.

$\mathbb{Q}$ ist sogar der kleinst mögliche Unterkörper von $\R$, d.h. jeder Unterkörper von $\R$ enthält mindestens $\mathbb{Q}$. Etwas allgemeiner enthält jeder Körper von Charakteristik 0 alle ganzen Zahlen (1+1+···+1) und deren Inverse, also $\mathbb{Q}$.

Endliche Körper

Hauptartikel: Endlicher Körper

Ein Körper ist ein endlicher Körper, wenn seine Grundmenge K endlich ist. Die endlichen Körper sind in folgendem Sinne vollständig klassifiziert: Jeder endliche Körper hat genau q = pⁿ Elemente mit einer Primzahl p und einer positiven natürlichen Zahl n. Bis auf Isomorphie gibt es zu jedem solchen q genau einen endlichen Körper, der mit 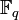$\Bbb F_q$ bezeichnet wird. Jeder Körper 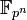$\Bbb F_{p^n}$ hat die Charakteristik p.

Im Spezialfall n = 1 erhalten wir zu jeder Primzahl p den Körper 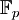$\Bbb F_p$, der isomorph zum Restklassenring 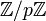$\mathbb{Z}/p \mathbb{Z}$ ist.

Verallgemeinerung: Schiefkörper

Hauptartikel: Schiefkörper

Verzichtet man auf die Bedingung, dass die Multiplikation kommutativ ist, so gelangt man zur Struktur des Schiefkörpers. Es gibt jedoch auch Autoren, die für einen Schiefkörper explizit voraussetzen, dass die Multiplikation nicht kommutativ ist. In diesem Fall ist ein Körper nicht mehr zugleich Schiefkörper. Ein Beispiel ist der Schiefkörper der Quaternionen, der kein Körper ist.

Geschichte

Wesentliche Ergebnisse der Körpertheorie sind Évariste Galois und Ernst Steinitz zu verdanken.

Siehe auch

• Charakteristik
• Vektorraum
• Körpererweiterung
• Formal reelle Körper

Literatur

• Siegfried Bosch: Algebra. 5. Auflage. Springer, 2004, ISBN 3-540-40388-4