Orthodrome

Der kürzeste Weg auf der Kugeloberfläche zwischen Punkt A und B ist eine Orthodrome.

Die Orthodrome (griech. orthos für „gerade“, dromos für „Lauf“) ist die kürzeste Verbindung zweier Punkte auf einer Kugeloberfläche.

Die Orthodrome ist immer ein Teilstück eines Großkreises. In der Luftfahrt fliegt man meist entlang dieser Orthodrome, um die geringste Flugstrecke zurücklegen zu müssen, daher auch die umgangssprachlich häufiger gebrauchte synonyme Bezeichnung Luftlinie.

Loxodrome

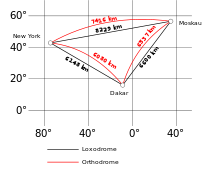Gegenüberstellung von Loxodrome und Orthodrome

Loxodromeverlängerung relativ zur Orthodrome entlang des 50. Breitengrades in Prozent.

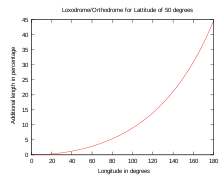
Bei der Navigation von Punkt A nach B mit einem Kompass eignet sich die Loxodrome besser, da sie immer mit dem gleichen Winkel die Meridiane kreuzt. Bei kurzen Strecken ist eine Loxodrome nur unwesentlich länger als eine Orthodrome. Bei hoher Breite und Entfernungen unterhalb von 30 Längengraden liegt der relative Längenunterschied bei weniger als 1%. Danach steigt er deutlich an. Eine Reise entlang des 50. Breitengrades über 180 Längengrade ist 45% länger als der Weg über einen Großkreis.

Berechnung

Grundlage für die folgenden Berechnungen sind die Formeln aus der sphärischen Trigonometrie.

Verwendete Variablen	Bedeutung
$\, \phi$	Geographische Breite
$\, \lambda$	Geographische Länge
$\, A (\phi_A, \lambda_A)$	Anfangspunkt
$\, B (\phi_B, \lambda_B)$	Endpunkt
$\, P_N(\phi_N, \lambda_N)$	Nördlichster Punkt der Orthodrome
$\, \alpha$	Kurswinkel bei A
$\, \beta$	Kurswinkel bei B
$\, \zeta$	Zentriwinkel (Strecke AB, ausgedrückt als Winkel)

Dabei ist $\, \lambda$ in Richtung Westen negativ, Richtung Osten positiv; $\, \phi$ ist positiv für Breiten der Nordhemisphäre und negativ auf der Südhalbkugel.

Nördlichster Punkt

In einer gnomonischen Projektion werden Orthodromen stets als gerade Strecke abgebildet

Berechnung des nördlichsten Punkts einer Orthodrome für einen Anfangspunkt A und einen Anfangs-Kurswinkel α:

$\, \phi_N = \arccos \left( \sin(|\alpha_A|) \cdot \cos(\phi_A) \right)$

$\lambda_N = \operatorname{sgn}(\alpha_A) \cdot \left| \arccos \left( \frac{\tan( \phi_A )}{\tan( \phi_N )}\right) \right|$

Strecke

Als Winkel lässt sich die Strecke folgendermaßen angeben:

$\, \zeta =\arccos\left(\sin(\phi_A) \cdot \sin(\phi_B) + \cos(\phi_A) \cdot \cos(\phi_B) \cdot \cos(\lambda_B - \lambda_A) \right)$

Um die Distanz zwischen den zwei Punkten zu berechnen, muss ζ noch mit dem Erdradius (rund 6.370 km) multipliziert werden (für ζ im Bogenmaß; falls ζ in Grad angegeben ist, muss noch zusätzlich mit 2π / 360 multipliziert werden).

Kurswinkel und rechtweisende Kurse

Kurswinkel

$\alpha = \arccos \left( \frac{\sin(\phi_B) - \sin(\phi_A) \cdot \cos(\zeta)} {\cos(\phi_A) \cdot \sin(\zeta)}\right)$

$\beta = \arccos \left( \frac{\sin(\phi_A) - \sin(\phi_B) \cdot \cos(\zeta)} {\cos(\phi_B) \cdot \sin(\zeta)}\right)$

Die beiden Parameter α und β lassen sich auch direkt aus den Breiten- und Längengraden ϕ_A bzw. ϕ_B und λ_A bzw. λ_B bestimmen:

$\alpha = \arccos \left( \frac{ \cos(\phi_A) \cdot \sin(\phi_B) - \cos(\lambda_A - \lambda_B) \cdot \cos(\phi_B) \cdot \sin(\phi_A) } {\sqrt{1- (\cos(\lambda_A - \lambda_B) \cdot \cos(\phi_A) \cdot \cos(\phi_B) + \sin(\phi_A) \cdot \sin(\phi_B))^2}} \right)$

$\beta = \arccos \left( \frac{ \cos(\phi_B) \cdot \sin(\phi_A) - \cos(\lambda_A - \lambda_B) \cdot \cos(\phi_A) \cdot \sin(\phi_B) } {\sqrt{1- (\cos(\lambda_A - \lambda_B) \cdot \cos(\phi_A) \cdot \cos(\phi_B) + \sin(\phi_A) \cdot \sin(\phi_B))^2}} \right)$

rechtweisende Kurse A → B

$\, rwK_A = \alpha$

$\, rwK_B = 180^\circ - \beta$

rechtweisende Kurse B → A

$\, rwK_B = 360^\circ - \beta$

$\, rwK_A = 180^\circ + \alpha$

Beispiel Berechnung der Entfernung Berlin–Tokio

Geographische Koordinaten der Anfangs- und Endpunkte:

• Berlin
  • 52° 31' 0" N = 52,517°
  • 13° 24' 0" E = 13,40°
• Tokio
  • 35° 42' 0" N = 35,70°
  • 139° 46' 0" E = 139,767°

Winkelberechnung

$\, \phi_A = 52{,}517^\circ$

$\, \lambda_A = 13{,}40^\circ$

$\, \phi_B = 35{,}70^\circ$

$\, \lambda_B = 139{,}767^\circ$

$\, \zeta =\arccos \Big( \sin(\phi_A) \sin(\phi_B) + \cos(\phi_A)\cos(\phi_B)\cos(\lambda_B - \lambda_A) \Big)$

$\, \zeta =\arccos \Big( \sin(52{,}517^\circ) \sin(35{,}70^\circ) + \cos(52{,}52^\circ)\cos(35{,}70^\circ)\cos(139{,}767^\circ - 13,40^\circ) \Big)$

$\, \zeta =\arccos(0{,}79353 \cdot 0{,}58354 + 0{,}60853 \cdot 0{,}81208 \cdot (-0{,}59296) )$

$\, \zeta =\arccos( 0{,}1700)$

$\, \zeta = 80{,}212^\circ$ bzw. $\, \zeta = 1{,}400$ (Bogenmaß)

Streckenberechnung

Zur Vereinfachung wird von einer Erdkugel mit U = 40.000 km bzw. 6.370 km Radius ausgegangen.

$L = \frac{\zeta}{360^\circ} \cdot 40\,000\ \mathrm{km}$

$L = \frac{80{,}212^\circ}{360^\circ} \cdot 40\,000\ \mathrm{km}$

$L = 8912\ \mathrm{km}$

Oder für $\, \zeta$ im Bogenmaß:

$L = \zeta \cdot 6370\ \mathrm{km}$

$L = 8918\ \mathrm{km}$

Das ist aufgrund der idealisierten Geodaten selbstverständlich nur eine Näherung. Die tatsächliche Entfernung zwischen den beiden angegebenen Punkten in Berlin und Tokyo kann bei Verwendung des WGS84-Referenzellipsoids zu 8941,2 km berechnet werden, also mit einer Abweichung von etwa 23 km oder 0,26 %.

Genauere Formel zur Abstandsberechnung auf der Erde

Mit folgenden Formeln kann der Abstand zwischen zwei Standorten auf der Erde auf 50 Meter genau berechnet werden. Dabei wird keine Kugel, sondern das WGS84-Ellipsoid zu Grunde gelegt. Sollten Koordinaten eines anderen Referenzellipsoiden verwendet werden, müssen die Parameter a (Radius) und f (Abplattung) angepasst werden.

Voraussetzung ist, dass der Abstand zwischen beiden Standorten ausreichend groß ist. Andernfalls kann eine Division durch Null auftreten. Außerdem müssen die trigonometrischen Funktionen (sin ,cos ) im Bogenmaß rechnen.

Seien b₁ die geografische Breite von Standort 1, l₁ die geografische Länge von Standort 1, b₂ die geografische Breite von Standort 2, l₂ die geografische Länge von Standort 2 im Gradmaß. Der Abstand zwischen beiden Standorten berechnet sich wie folgt:

Abplattung der Erde: $f := \frac{1}{298{,}257\,223\,563}$

Äquatorradius der Erde in Kilometern: $a := \frac{6\,378\,137}{1000}$

$F := \frac{b_1 + b_2}{2}$, $G := \frac{b_1 - b_2}{2}$, $l := \frac{l_1 - l_2}{2}$

Die Parameter müssen nun in das Bogenmaß umgerechnet werden:

$F := \frac{\pi}{180} \cdot F$, $G := \frac{\pi}{180} \cdot G$, $l := \frac{\pi}{180} \cdot l$

Nun wird der grobe Abstand D ermittelt:

$S := (\sin{G})^2 \cdot (\cos{l})^2 + (\cos{F})^2 \cdot (\sin{l})^2$

$C := (\cos{G})^2 \cdot (\cos{l})^2 + (\sin{F})^2 \cdot (\sin{l})^2$

$w := \arctan{\sqrt{\frac{S}{C}}}$

$D := 2 \cdot w \cdot a$

Der Abstand D muss nun durch die Faktoren H₁ und H₂ korrigiert werden:

$R := \frac{\sqrt{S \cdot C}}{w}$

$H_1 := \frac{ 3 \cdot R - 1}{2 \cdot C}$

$H_2 := \frac{3 \cdot R + 1}{2 \cdot S}$

Der Abstand s in Kilometern berechnet sich abschließend wie folgt:

$s := D \cdot \left(1 + f \cdot H_1 \cdot (\sin{F})^2 \cdot (\cos{G})^2 - f \cdot H_2 \cdot (\cos{F})^2 \cdot (\sin{G})^2 \right)$

Berechnungsbeispiel Berlin – Tokio

   b1 := 52,5167
   l1 := 13,4000
   b2 := 35,7000
   l2 := 139,7667

   f := 0,003352811
   a := 6378,137

   F := 44,10833333
   G := 8,408333333
   l := -63,18333333
   S := 0,414982619
   C := 0,585017381
   w := 0,699965691
   R := 0,703918833
   D := 8928,958342
   H1 := 0,950190999
   H2 := 3,749261245

   s := 8941,201228 km

Siehe auch

• Geodätische Linie
• Abweitung

Weblinks

• Berechnung der Entfernung zwischen zwei geographischen Koordinaten
• Berechnung der Entfernung zwischen zwei oder mehr Orten auf der Erde mit Kartendarstellung (englisch)
• Great Circle Mapper - Great Circle mapper including ETOPS ranges (englisch)
• Abstandsberechnung am WGS84 Ellipsoid - Konkrete Umsetzung des Problems in PHP (als PDF)

Quellen

Formel zur genaueren Abstandsberechnung:

• Meeus, J.: Astronomical Algorithms, S 85, Willmann-Bell, Richmond 2000 (2nd ed., 2nd printing), ISBN 0-943396-61-1

• Loxodrome