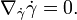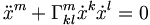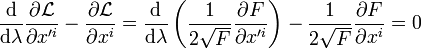Geodätengleichung

Kürzeste Verbindung auf einer Kugeloberfläche, aufgetragen über dem Gradnetz (Orthodrome)

Geodäten (rot) in einem zweidimensionalen gekrümmten Raum, der in einem dreidimensionalen Raum eingebettet ist

Eine Geodäte (Pl. Geodäten), auch Geodätische, geodätische Linie oder geodätischer Weg genannt, ist die lokal kürzeste Verbindungskurve zweier Punkte.

Im euklidischen Raum sind Geodäten stets Geraden. Relevant ist der Begriff „Geodäte“ erst in gekrümmten Räumen (Mannigfaltigkeiten), wie zum Beispiel auf einer Kugeloberfläche oder anderen gekrümmten Fläche oder auch in der gekrümmten Raumzeit der allgemeinen Relativitätstheorie. Man findet die geodätischen Linien mit Hilfe der Variationsrechnung.

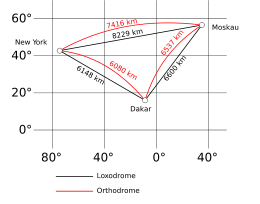
Die Einschränkung „lokal“ in der obigen Definition bedeutet, dass eine Geodäte nur dann die kürzeste Verbindung zwischen zwei Punkten zu sein braucht, wenn diese Punkte nahe genug beieinander liegen; sie muss aber nicht den global kürzesten Weg darstellen. Beispielsweise ist die kürzeste Verbindung zwischen zwei Punkten auf der Erdoberfläche stets Teil eines Großkreises, aber die beiden Teile, in die ein Großkreis durch zwei Punkte unterteilt wird, sind beide Geodäten, obwohl nur einer der beiden die „global“ kürzeste Verbindung darstellt.

• Eine Geodäte auf der (als Kugel genäherten) Erdoberfläche ist stets Teil eines Großkreises; daran orientieren sich transkontinentale Flug- und Schifffahrtsrouten (siehe Orthodrome).

• In der elementaren Differentialgeometrie ist eine Geodäte ein Weg auf einer Fläche, bei dem überall die Hauptnormale mit der Flächennormale zusammenfällt. Diese Bedingung ist genau dann erfüllt, wenn in jedem Punkt die geodätische Krümmung gleich 0 ist.

• Im Sonderfall abwickelbarer Flächen (z. B. Kegel oder Zylinder) sind die Geodäten diejenigen Kurven, die bei der Abwickelung in die Ebene zu Geradenstücken werden.

• In der modernen Sprache der riemannschen Geometrie sind Geodäten γ durch eine Differentialgleichung charakterisiert:

$\nabla_{\dot\gamma}\dot\gamma=0.$

Dabei bezeichnet $\nabla$ den Levi-Civita-Zusammenhang.

Diese Gleichung bedeutet, dass das Geschwindigkeitsvektorfeld der Kurve längs der Kurve konstant ist. Anschaulich ausgedrückt: Wer der Kurve folgt, der geht im Sinne der riemannschen Metrik „geradeaus“.

• In der „klassischen“ Sprache der Differentialgeometrie, die in der allgemeinen Relativitätstheorie benutzt wird, lautet diese Differentialgleichung:

$\ddot x^m+\Gamma^m_{kl}\dot x^k\dot x^l=0$

Dabei sind die 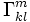$\Gamma^m_{kl}$ die Christoffelsymbole und x eine lokale Koordinatendarstellung des entsprechenden Weges.

Diese Differentialgleichungen ergeben sich mit Hilfe der Variationsrechnung.

Die Geodätengleichung

Mit Hilfe der Variationsrechnung lässt sich die Geodätengleichung herleiten. Ausgangspunkt ist dabei die Eigenschaft einer Geodäte, die kürzeste Verbindung zweier Punkte zu sein. Im gekrümmten Raum fragen wir also nach derjenigen Kurve, deren Bogenlänge s bei gegebenen Anfangs- und Endpunkt ein Minimum annimmt, also

$s=\int\limits_{P_A}^{P_E}\mathrm{d}s\stackrel{!}=\text{Extremum}$.

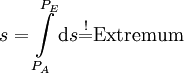Die Kurve sei mit dem Parameter λ parametrisiert und das Linienelement ist allgemein gegeben durch ds² = g_ikdxⁱdx^k. Dabei erhält der Raum, welcher die Kurve beinhaltet, durch den metrischen Tensor g_ik ein Maß für Winkel und Abstände. Somit erhalten wir aus obigem Ansatz

$s=\int\limits_{\lambda_E}^{\lambda_A}\frac{\mathrm{d}s}{\mathrm{d}\lambda}\mathrm{d}\lambda=\int\limits_{\lambda_E}^{\lambda_A}\sqrt{g_{ik}\frac{\mathrm{d}x^{i}}{\mathrm{d}\lambda}\frac{\mathrm{d}x^{k}}{\mathrm{d}\lambda}}\mathrm{d}\lambda=\text{Extremum}$.

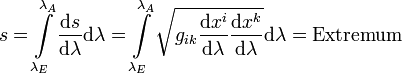Diese Gleichung ist in ihrer Form analog dem Hamiltonprinzip mit einer Lagrangefunktion

$\mathcal{L}=\sqrt{g_{ik}\frac{\mathrm{d}x^{i}}{\mathrm{d}\lambda}\frac{\mathrm{d}x^{k}}{\mathrm{d}\lambda}}=\sqrt{g_{ik}x'^{i}x'^{k}}=\sqrt{F},\quad\text{mit}\quad x'^{i}=\frac{\mathrm{d}x^{i}}{\mathrm{d}\lambda}$.

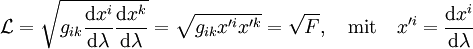Sie muss demnach die Euler-Lagrange-Gleichung erfüllen, also

$\frac{\mathrm{d}}{\mathrm{d}\lambda}\frac{\partial\mathcal L}{\partial x'^{i}}-\frac{\partial\mathcal{L}}{\partial x^{i}}=\frac{\mathrm{d}}{\mathrm{d}\lambda}\left(\frac{1}{2\sqrt{F}}\frac{\partial F}{\partial x'^{i}}\right)-\frac{1}{2\sqrt{F}}\frac{\partial F}{\partial x^{i}}=0$

Siehe auch

• Riemannsche Mannigfaltigkeit