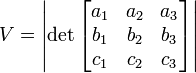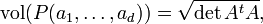Parallelotop

Unter einem Parallelepiped (von griechisch επίπεδο, epipedo = Fläche) (Synonyme: Spat, Parallelflach, Parallelotop) versteht man einen geometrischen Körper, der von sechs paarweise kongruenten (deckungsgleichen) in parallelen Ebenen liegenden Parallelogrammen begrenzt wird. Die Bezeichnung Spat rührt vom Kalkspat (Calcit, chemisch: CaCO₃) her, dessen Kristalle die Form eines Parallelflachs aufweisen.

Ein Parallelepiped hat zwölf Kanten, von denen je vier parallel verlaufen und untereinander gleich lang sind. Stellt man drei an einem Eckpunkt zusammentreffende Kanten als Vektoren $\vec a, \vec b, \vec c$ dar, so ergibt sich das Volumen des Parallelflachs aus dem Betrag des Spatproduktes (gemischtes Skalar- und Kreuzprodukt)

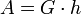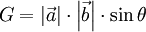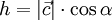Das Volumen A ist das Produkt der Grundfläche G und der Parallelepiped-Höhe h, $A = G \cdot h$ mit $G = \left|\vec a \right| \cdot \left|\vec b \right| \cdot \sin \theta$ (mit θ als Winkel zwischen $\vec a$ und $\vec b$) und der Höhe $h = \left| \vec c \right| \cdot \cos \alpha$. Dabei ist α der Winkel zwischen 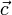$\vec c$ und der Höhe h.

Das Volumen kann man auch als Determinante einer 3×3-Matrix ansehen, das man auch Spatprodukt nennt.

$V = \left| \det \begin{bmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{bmatrix} \right|$

Die Oberfläche ergibt sich aus der Summe der einzelnen Parallelogrammflächen: $A_O = 2 \cdot \left(\left| \vec a \times \vec b \right|+\left| \vec a \times \vec c \right|+\left| \vec b \times \vec c \right|\right)$.

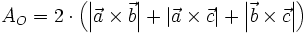Quader und Würfel sind Sonderformen des Parallelflachs.

Das Parallelepiped ist ein spezielles (schiefes) Prisma mit einem Parallelogramm als Grundfläche. Sind die Parallelogramme sogar Rauten, spricht man von einem Rhomboeder.

Jedes Parallelepiped ist ein Raumfüller, das heißt der Raum lässt sich mit parallelverschobenen Exemplaren von P so überdecken, dass je zwei unter ihnen höchstens Randpunkte gemein haben.

Verallgemeinerung auf den n-dimensionalen Raum (n > 1)

Ein n-dimensionales Parallelepiped P ist ein affines Bild des Einheitswürfels E (der aus allen Punkten mit Koordinaten zwischen 0 und 1 (einschließlich) besteht). P ist insbesondere ein konvexes Polytop mit 2ⁿ Ecken. Für m < n sind seine m-dimensionalen Seiten selbst m-dimensionale Parallelepipede. Da P aus E durch eine affine Abbildung entsteht, ist sein orientiertes, also positives oder negatives, Volumen gleich der Determinante dieser Abbildung. Auch in diesem allgemeinen Fall ist P ein Raumfüller. Für n=2 ergibt sich das Parallelogramm.

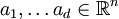Wenn $P(a_1, \dots , a_d) := \Biggl\{ \sum^{d}_{i=1} t_i a_i | t_1, \dots , t_d \in [0,1] \Biggr\}$ das von $a_1, \dots a_d \in \R^n$ aufgespannte d-dimensionale Parallepiped ist, dann gilt für das Volumen von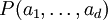 $P(a_1, \dots , a_d)$

$\mathrm{vol}(P(a_1, \dots , a_d))=\sqrt{ \det A^t A },$

wobei die Spalten der Matrix A durch die Vektoren 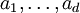$a_1, \dots , a_d$ gegeben sind.

Literatur

• Konrad Königsberger: Analysis. Band 2. Springer, Berlin 2004, ISBN 3-540-20389-3.