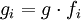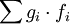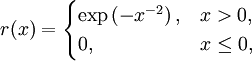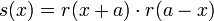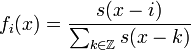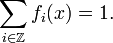Partition der Eins

In der Mathematik gibt es oft Situationen, in welchen zwischen einer lokalen und einer globalen Perspektive unterschieden werden muss, aber zwischen beiden hin- und hergewechselt werden soll. Zum Beispiel:

• Um in der Analysis das Flächenintegral zu definieren, oder allgemein über Mannigfaltigkeiten zu integrieren, müssen Koordinaten gewählt werden, was nur lokal möglich ist. Der Integrand muss also so zerlegt werden, dass er lokal integrabel bleibt, außerhalb des Geltungsbereiches des Koordinatensystems aber zu Null wird.

• In der Differentialgeometrie werden auf Flächen oder Mannigfaltigkeiten Vektorfelder konstruiert. Es gibt oft nur lokal gültige Konstruktionen, die aber zu einer globalen zusammengefügt werden sollen. Zum Beispiel soll das Normalenfeld einer Untermannigfaltigkeit auf die gesamte Mannigfaltigkeit fortgesetzt werden,...

• In der Lösungstheorie partieller Differentialgleichungen kann die Lösung einer partiellen Differentialgleichung auf einem beliebigen Gebiet häufig mit Hilfe der Zerlegung der Eins durch Lösungen der Gleichung auf dem Ganzraum und dem (gestörten) Halbraum zusammengesetzt werden (sog. Lokalisierung).

Eine Zerlegung der Eins (auch: Unterteilung der Einheit oder Teilung der Eins) über einem topologischen Raum E ist eine Familie (f_i) stetiger Funktionen von E in das Intervall [0,1], so dass für jeden Punkt x aus E gilt:

• x hat eine Umgebung, in der nur endlich viele Funktionen einen von 0 verschiedenen Wert haben; und
• die Summe aller Funktionswerte im Punkt x ist 1.

Die Zerlegung der Eins ist ein wichtiges Hilfsmittel der Analysis. Dort wird meist noch verlangt, dass die Funktionen differenzierbar sind und kompakten Träger haben. Damit kann dann eine Funktion g in Funktionen

$g_i = g\cdot f_i$

zerlegt werden, welche alle einen kompakten Träger haben. Ist hingegen eine Familie (g_i) vorgegeben, welche nur auf den jeweiligen Trägern der f_i definiert und differenzierbar sind, so ist die Summe

$\sum g_i \cdot f_i$

eine konvexe Linearkombination, überall definiert und differenzierbar.

In parakompakten Hausdorff-Räumen ist eine (stetige) Zerlegung der Eins immer möglich. Jede parakompakte C^k-Mannigfaltigkeit (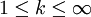$1\leq k\leq \infty$) besitzt auch eine C^k-Zerlegung der Eins.

Analytische Zerlegungen der Eins sind jedoch nicht möglich, da eine analytische Funktion, die in einer nichtleeren, offenen Menge (wie etwa dem Komplement ihres Trägers) konstant 0 ist, bereits überall konstant 0 ist.

Beispiele

Sei $a \in \left]\frac{1}{2};1\right[$ beliebig (z.B. a = 0,9). Die Funktion

$r(x)=\begin{cases} \exp \left(- x^{-2} \right), & x > 0,\\ 0, & x \le 0,\end{cases}$

ist beliebig oft differenzierbar. Die Funktion s mit

$s(x) = r (x+a) \cdot r(a-x)$

ist dann ebenfalls beliebig oft differenzierbar, strikt positiv im Intervall (-a; a) und gleich null außerhalb. Die Funktionen 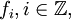$f_i, i \in \mathbb{Z},$ mit

$f_i(x)= \frac{s(x-i)}{\sum_{k \in \mathbb{Z}} s(x-k)}$

bilden nun eine beliebig oft differenzierbare Zerlegung der Eins auf der reellen Achse, die der offenen Überdeckung 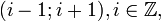$(i - 1; i + 1), i \in \mathbb{Z},$ untergeordnet ist; es gilt also an jedem Punkt x:

$\sum_{i \in \Z} f_i(x)=1.$

Man beachte, dass in der Definition von f_i an jeder Stelle x immer mindestens ein Summand und höchstens zwei Summanden im Nenner ungleich null sind (nur die zu x benachbarten ganzen Zahlen k können überhaupt einen positiven Summanden liefern).