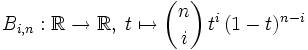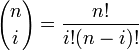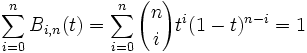- Bernsteinpolynome
-
Die Bernsteinpolynome sind eine Familie reeller Polynome mit ganzzahligen Koeffizienten. Sie haben ihren Ursprung in der Approximationstheorie. Mit ihrer Hilfe konnte ihr Entdecker Sergei Natanowitsch Bernstein im Jahre 1911 einen konstruktiven Beweis für den Approximationssatz von Weierstraß angeben. Ende der 1950er Jahre gab es erste Versuche, auf Bernsteinpolynomen basierende Methoden im Design von Kurven und Flächen einzusetzen. Paul de Faget de Casteljau bei Citroën und Pierre Bézier bei Renault nutzten die Bernsteinpolynome bei ihrer Entwicklung von Bézierkurven und legten damit den Grundstein des heutigen Computer Aided Design (CAD).
Inhaltsverzeichnis
Definition
Für
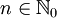 heißen die reellen Polynome
heißen die reellen Polynome(mit
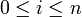 ) die Bernsteinpolynome vom Grad n.
) die Bernsteinpolynome vom Grad n.Durch affine Transformation (Abbildung des Intervalls [0,1] auf ein beliebiges Intervall [a,b]) erhält man die verallgemeinerten Bernsteinpolynome
![B_{i,n}^{[a,b]}:\R \to \R,\; t \mapsto \frac{1}{(b-a)^n} {n \choose i} (t-a)^i\, (b-t)^{n-i}](/pictures/dewiki/53/54f0c5e0cbc9e61ceaddb61054ae6ea2.png) .
.
Dabei bezeichnet
Beispiel
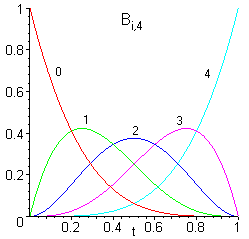
Die folgende Abbildung zeigt die Bernsteinpolynome Bi,4,
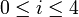 vom Grad 4:
vom Grad 4:Eigenschaften
Die Bernsteinpolynome bezüglich des Intervalls [0,1] haben folgende Eigenschaften:
- Basiseigenschaft: Die Bernsteinpolynome
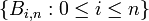 sind linear unabhängig und bilden eine Basis von Πn, dem Raum der Polynome vom Grad kleiner oder gleich n.
sind linear unabhängig und bilden eine Basis von Πn, dem Raum der Polynome vom Grad kleiner oder gleich n. - Positivität:
- Bi,n(t) > 0 für alle
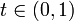 .
.
- Bi,n(t) > 0 für alle
- Extrema: Bi,n besitzt im Intervall [0,1] genau ein (absolutes) Maximum. Es befindet sich an der Stelle
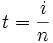 . Man erhält insbesondere:
. Man erhält insbesondere:
- B0,n(0) = Bn,n(1) = 1
- Zerlegung der Eins (auch Partition der Eins):
- (Ergibt sich mit Hilfe des binomischen Lehrsatzes aus (t + (1 − t))n.)
- Symmetrie:
- Bi,n(t) = Bn − i,n(1 − t)
- Rekursionsformel:
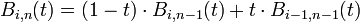 , mit der Definition
, mit der Definition- Bi,n: = 0 für i < 0 oder i > n
- B0,0: = 1
- Gradanhebung:
- Ableitungen:
![B'_{i,n}(t) = n \left[ B_{i-1,n-1}(t) - B_{i,n-1}(t) \right]](/pictures/dewiki/56/8842b4e01045d4c83f901ad7ad0c8a31.png) , mit der Definition
, mit der Definition- B − 1,n − 1 = Bn,n − 1: = 0
Approximation durch Bernsteinpolynome
Für eine Funktion
![f: [0,1] \to \R](/pictures/dewiki/101/e1e8eaf7fd9f12d440ba424134f0b3b8.png) heißt das durch
heißt das durch 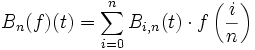 definierte Polynom Bn(f) das n-te Bernsteinpolynom der Funktion f.
definierte Polynom Bn(f) das n-te Bernsteinpolynom der Funktion f.Ist f eine stetige Funktion auf dem Interval [0,1], so konvergiert die Folge ihrer Bernsteinpolynome Bn(f) gleichmäßig gegen f.
Weblinks
Literatur
- Bernstein, S.N., Démonstration du Théorème de Weierstrass fondée sûr le calcul dés Probabilités, Commun. Soc. Math. Kharkow, Vol. 12, No. 2, pp. 1-2, 1912.
Wikimedia Foundation.