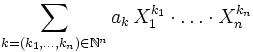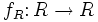- Polynomalgebra
-
Unter dem Polynomring R[X] versteht man anschaulich die Menge aller Polynome mit Koeffizienten aus einem Ring R und der Variablen X. Da man, wie in den Beispielen erläutert, nicht immer alle Polynome mit Polynomfunktionen identifizieren kann, muss im folgenden exakt definiert werden, was ein Polynomring sein soll.
Inhaltsverzeichnis
Definition
Ausgehend von einem kommutativen Grundring R kann man den Polynomring als den Raum
der endlichen Folgen in R definieren, ausgestattet mit der komponentenweisen Addition
und der durch die Faltung definierten Multiplikation
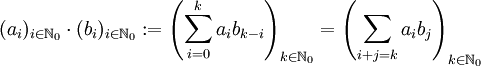 .
.
Durch diese Verknüpfungen wird auf dem Raum der endlichen Folgen eine Ringstruktur definiert.
Falls R unitär ist (d. h. ein Einselement 1 besitzt), so ist die Folge
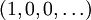 das Einselement in
das Einselement in 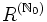 , außerdem besitzt der Polynomring dann einen multiplikativen Erzeuger
, außerdem besitzt der Polynomring dann einen multiplikativen Erzeuger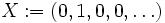 .
.
Mit dem Erzeuger X kann nun jedes Element f aus
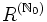 eindeutig in der geläufigen Polynomschreibweise
eindeutig in der geläufigen Polynomschreibweisedargestellt werden.
Damit erhält man den Polynomring R[X] über R in der Unbestimmten X; generell wird anstelle der Schreibweise
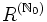 die Bezeichnung R[X] bevorzugt. Die einzelnen Folgenglieder ai nennt man die Koeffizienten des Polynoms; als den Grad des Polynoms bezeichnet man den größten Index n, für den der Koeffizient an nicht 0 ist.
die Bezeichnung R[X] bevorzugt. Die einzelnen Folgenglieder ai nennt man die Koeffizienten des Polynoms; als den Grad des Polynoms bezeichnet man den größten Index n, für den der Koeffizient an nicht 0 ist.Ist R faktoriell, so auch R[X] (Satz von Gauß), ist R ein Körper, so ist insbesondere R[X] ein Hauptidealring.[1]
Eigenschaften
Elementare Operationen, Polynomalgebra
In der Polynomschreibweise sehen Addition und Multiplikation für Elemente
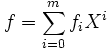 und
und 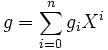 des Polynomrings R[X] wie folgt aus:
des Polynomrings R[X] wie folgt aus: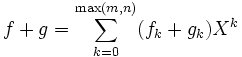 ,
,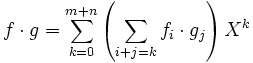 .
.
Der Polynomring R[X] ist nicht nur ein kommutativer Ring, sondern auch ein Modul über R, wobei die skalare Multiplikation gliedweise definiert ist. Damit ist R[X] sogar eine kommutative assoziative Algebra über R.
Homomorphismen
Falls A und B kommutative Ringe sind und
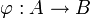 ein Homomorphismus ist, dann ist auch
ein Homomorphismus ist, dann ist auch![\phi:A[X]\to B[X],\quad \sum_{i=1}^{n} {a_iX^i}\,\mapsto\,\sum_{i=1}^{n} \varphi (a_i)X^i](/pictures/dewiki/98/b199900bb539f466504ca980ff775acf.png) ein Homomorphismus.
ein Homomorphismus.
Falls A und B kommutative Ringe sind und
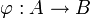 ein Homomorphismus ist, dann gibt es für jedes
ein Homomorphismus ist, dann gibt es für jedes 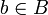 einen eindeutigen Homomorphismus
einen eindeutigen Homomorphismus ![\psi:A[X]\to B](/pictures/dewiki/55/7363742ec86e32bf43fc27ea3349bcb3.png) , der eingeschränkt auf A gleich
, der eingeschränkt auf A gleich  ist und für den ψ(X) = b gilt, nämlich
ist und für den ψ(X) = b gilt, nämlich 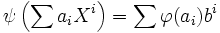 .
.Polynomfunktion und Einsetzungshomomorphismus
Ist
ein Polynom aus R[X], so nennt man
die zu f gehörende Polynomfunktion. Allgemeiner definiert f auch für jede Erweiterung S von R eine Polynomfunktion
 Der Index wird oft weggelassen.
Der Index wird oft weggelassen.Umgekehrt gibt es für ein festes Element
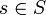 bei variablem Polynom einen Ringhomomorphismus
bei variablem Polynom einen Ringhomomorphismusbzw.
der Auswertung(-shomomorphismus) für s oder Einsetzung(-shomomorphismus) von s genannt wird.
Beispiele
- Setzen wir S = R[X] und s = X, so ist
![\Phi_X\colon R[X] \rightarrow R[X],\ f\mapsto f_{R[X]}(X)=f](/pictures/dewiki/101/eb1785188f36119bf80d6415153d0223.png) die identische Abbildung;
die identische Abbildung; ![\Phi_X = \operatorname{Id}_{R[X]}.](/pictures/dewiki/99/c03f0a0dd7ad1487796e13772f64dde1.png)
- Betrachten wir einen Polynomring
![R[X, X_1, X_2, \ldots, X_n]](/pictures/dewiki/102/f37e80d68c642da8671c27ec82d2ee5b.png) mit zusätzlichen Unbestimmten
mit zusätzlichen Unbestimmten 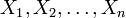 (s. Polynome mit mehreren Veränderlichen) als Erweiterung von R[X], ergibt sich analog zur Konstruktion aus vorigem Beispiel der Einsetzungshomomorphismus
(s. Polynome mit mehreren Veränderlichen) als Erweiterung von R[X], ergibt sich analog zur Konstruktion aus vorigem Beispiel der Einsetzungshomomorphismus ![\Phi_X\colon R[X] \rightarrow R[X,Y],\ f\mapsto f_{R[X,Y]}(X)=f](/pictures/dewiki/52/4919d5be208ff314e48a1764bb2e2a8e.png) als Monomorphismus von R[X] in
als Monomorphismus von R[X] in ![R[X, X_1, X_2, \ldots, X_n].](/pictures/dewiki/54/660733580e936e30d462c6de4feb5067.png)
Polynome mit mehreren Veränderlichen
In vielen Fällen, zum Beispiel in der algebraischen Geometrie, benötigt man Polynome mit mehreren unabhängigen Veränderlichen. Den dafür zugrundeliegenden Polynomring kann man iterativ so definieren:
Man betrachtet hier also Polynome in der Variablen Xn mit Koeffizienten aus dem Polynomring
![R[X_1,\ldots X_{n-1}]](/pictures/dewiki/50/2ab7e8d0ecd145ce35f29c74be7fcefc.png) , wobei dieser wieder genauso definiert ist. Dies kann man solange fortsetzen, bis man bei der Definition des Polynomrings in einer Veränderlichen angekommen ist. Einsetzungshomomorphismus und Polynomfunktion werden hier analog definiert, und in
, wobei dieser wieder genauso definiert ist. Dies kann man solange fortsetzen, bis man bei der Definition des Polynomrings in einer Veränderlichen angekommen ist. Einsetzungshomomorphismus und Polynomfunktion werden hier analog definiert, und in ![R[X_1,\ldots X_n]](/pictures/dewiki/98/bf88059e49f3486b6276678c083a3b88.png) kann man jedes Element eindeutig als
kann man jedes Element eindeutig alsschreiben.
Der Polynomring in beliebig vielen Unbestimmten (mit einer Indexmenge J) kann entweder als der Monoidring über dem freien kommutativen Monoid über J oder als die Vereinigung (der Kolimes) der Polynomringe für endliche Teilmengen von J definiert werden.
Beispiele
Ein Polynom über einem endlichen Körper
Sei p eine Primzahl und
![R=\mathbb{Z}/p\mathbb{Z},~f(X)=X^p-X\in R[X]](/pictures/dewiki/53/52a10d579404c0a3205d28070c956455.png) . Dann ist f nicht das Nullpolynom, aber die zugehörige Polynomfunktion
. Dann ist f nicht das Nullpolynom, aber die zugehörige Polynomfunktionist die Nullfunktion, da in
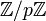 für jedes Element x die Gleichung xp = x gilt (kleiner fermatscher Satz).
für jedes Element x die Gleichung xp = x gilt (kleiner fermatscher Satz).Grundsatz nach Assoziativität!
Ein Polynom mit zwei Veränderlichen
Sei
![f=X^2+Y^2-1 \in \mathbb{R}[X,Y]](/pictures/dewiki/52/4d4e54b165f5bbaacb451edf9e4ef0a4.png) . Die reellen Nullstellen dieses Polynoms sind alle Punkte der Einheitskreislinie, in Formeln
. Die reellen Nullstellen dieses Polynoms sind alle Punkte der Einheitskreislinie, in Formeln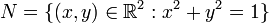 .
.
Es gibt hier also unendlich viele Nullstellen, anders als in
![\mathbb{Z}[X]](/pictures/dewiki/56/8948f9796109cbb4f99d4dd5ba0b3b82.png) oder
oder ![\mathbb{R}[X]](/pictures/dewiki/53/5e11093b37fd30fbaa413f6bdf9647c4.png) , wo jedes Polynom nur endlich viele Nullstellen hat.
, wo jedes Polynom nur endlich viele Nullstellen hat.Polynome im Komplexen
Jedes komplexe Polynom
![f\in \Bbb C[X]](/pictures/dewiki/49/1c6a2a1fa6637cdb5a91c0162d564662.png) vom Grad n hat genau n Nullstellen in
vom Grad n hat genau n Nullstellen in  , wenn man jede Nullstelle gemäß ihrer Vielfachheit zählt. Dabei heißt eine Nullstelle z k-fach, falls (x − z)k ein Teiler von f ist, (x − z)k + 1 dagegen nicht mehr.
, wenn man jede Nullstelle gemäß ihrer Vielfachheit zählt. Dabei heißt eine Nullstelle z k-fach, falls (x − z)k ein Teiler von f ist, (x − z)k + 1 dagegen nicht mehr.Insbesondere gilt dieser Fundamentalsatz der Algebra auch für reelle Polynome
![f\in\R[X]](/pictures/dewiki/53/5cb4b687c86294d1beb3c0aacf0dfbf7.png) , wenn man diese als Polynome in
, wenn man diese als Polynome in ![\Bbb C[X]](/pictures/dewiki/52/430f7f19a53d123a7bed1a449b2a7c87.png) auffaßt. Zum Beispiel hat das Polynom X2 + 1 die Nullstellen i und − i, da i2 = − 1 und ebenso ( − i)2 = − 1, also gilt X2 + 1 = (X + i)(X − i).
auffaßt. Zum Beispiel hat das Polynom X2 + 1 die Nullstellen i und − i, da i2 = − 1 und ebenso ( − i)2 = − 1, also gilt X2 + 1 = (X + i)(X − i).Polynomringe über Körpern
Ein Polynomring in einer Variablen über einem Körper ist ein Hauptidealring. Ein Polynomring in mehreren Variablen über einem Körper ist ein noetherscher Ring. Dies folgt aus dem hilbertschen Basissatz.
Verallgemeinerung
Den Begriff des Polynomrings kann man zu einem Monoidring verallgemeinern.
Literatur
- Albrecht Beutelspacher: Lineare Algebra (Vieweg 2003, 6. Auflage, ISBN 352856508X )
- ↑ Gerd Fischer: Lehrbuch der Algebra. Vieweg, Wiesbaden 2008, ISBN 9783834802262
Wikimedia Foundation.

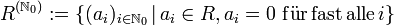
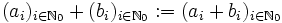
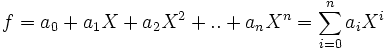
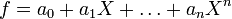
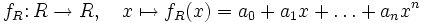
![\Phi_s\colon R[X] \rightarrow S,\quad f\mapsto f_S(s)](/pictures/dewiki/56/8e3735efe017f2d1a4d272308c758359.png)
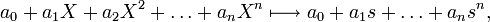
![R[X_1,\ldots,X_n]:=R[X_1,\ldots,X_{n-1}][X_n]](/pictures/dewiki/56/8d30198726af86934025a751e7568a4b.png)