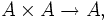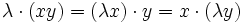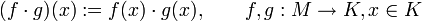Unteralgebra

Algebra über einem Körper

berührt die Spezialgebiete

Mathematik Abstrakte Algebra Lineare Algebra Kommutative Algebra

ist Spezialfall von

Algebraische Struktur Vektorraum

umfasst als Spezialfälle

Assoziative Algebra Kommutative Algebra Lie-Algebra Divisionsalgebra Banachalgebra und viele andere

Eine Algebra A über einem Körper K oder kurz K-Algebra ist ein K-Vektorraum mit einer K-bilinearen Verknüpfung

$A\times A\to A,$

Multiplikation genannt, die durch x · y oder xy symbolisiert wird. (Diese Verknüpfung ist unabhängig von der Multiplikation im Körper und derjenigen von Körperelementen mit Vektoren; die Verwendung desselben Symbols führt jedoch nicht zu Verwechslungen, da aus dem Kontext hervorgeht, welche Verknüpfung gemeint ist.) In älteren Algebra-Büchern wird eine Algebra über einem Körper auch als lineare Algebra bezeichnet^[1].

Allgemeiner kann K ein kommutativer Ring sein, dann ist „Vektorraum“ durch „Modul“ zu ersetzen, und man erhält eine Algebra über einem kommutativen Ring.

Explizit bedeutet das für Elemente x, y, z von A und Skalare λ in K:

• $(x+y)\cdot z = xz + yz$
• $x\cdot(y+z) = xy + xz$
• $\lambda\cdot(xy) = (\lambda x)\cdot y = x\cdot (\lambda y)$

Weitere Attribute und Beispiele

Eine assoziative Algebra ist eine K-Algebra, in der für die Multiplikation das Assoziativgesetz gilt. Beispiele:

• Die Algebra der 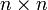$n\times n$ Matrizen über einem Körper; die Multiplikation ist hierbei die Matrizenmultiplikation.
• Die Inzidenzalgebra einer partiell geordneten Menge.
• Algebren von linearen Operatoren von einem K-Vektorraum in sich selbst; die Multiplikation ist hier die Hintereinanderausführung.
• Die Gruppenalgebra K[G] zu einer Gruppe G; hierbei bilden die Gruppenelemente eine K-Basis_(Vektorraum) des K-Vektorraums K[G], und die Algebra-Multiplikation ist die bilineare Fortsetzung der Gruppenmultiplikation.

Eine kommutative Algebra ist eine K-Algebra, in der für die Multiplikation das Kommutativgesetz gilt. Beispiele:

• Die (assoziative) Algebra K[x] der Polynome mit Koeffizienten in K in einer Unbekannten x.
• Die (ebenfalls assoziative) Algebra K[x₁,...,x_n] der Polynome mit Koeffizienten in K in mehreren Unbekannten x₁,...,x_n.
• Eine Funktionenalgebra erhält man, indem man einen Funktionenraum von Funktionen von einer Menge M in einen Körper K mit folgender punktweisen Multiplikation versieht:

$(f\cdot g)(x) := f(x)\cdot g(x),\qquad f,g:M\to K, x\in K$

Funktionenalgebren sind assoziativ, weil die zugrunde liegende Körpermultiplikation assoziativ ist.

• Genetische Algebren sind kommutative Algebren mit einigen zusätzlichen Eigenschaften, in denen das Assoziativgesetz im Allgemeinen nicht erfüllt ist.

Eine unitäre Algebra ist eine Algebra mit einem neutralen Element der Multiplikation, dem Einselement (vgl. unitärer Ring. Beispiele:

• Matrizenalgebren mit der Einheitsmatrix als Einselement.
• Jede Gruppenalgebra ist unitär: das Einselement der Gruppe ist auch Einselement der Algebra.
• Das konstante Polynom 1 ist Einselement einer Polynomalgebra.
• Der Körper K mit seiner Körpermultiplikation als Algebra-Multiplikation ist als K-Algebra assoziativ, kommutativ und unitär.

Wenn das aus dem jeweiligen Kontext klar ist, werden die Eigenschaften „assoziativ“, „kommutativ“ und „unitär“ in der Regel nicht explizit genannt.

Manche Autoren bezeichnen eine K-Algebra als nicht-assoziativ, wenn das Assoziativgesetz nicht vorausgesetzt wird^[2]. (Diese Begriffsbildung führt allerdings zu der etwas verwirrenden Konsequenz, dass insbesondere jede assoziative Algebra auch nicht-assoziativ ist.) Einige Beispiele für Algebren, die nicht notwendigerweise assoziativ sind:

• Eine Divisionsalgebra ist eine Algebra, in der man „dividieren“ kann, d.h. in der alle Gleichungen ax = b und ya = b für a ≠ 0 stets eindeutig lösbar sind. Eine Divisionsalgebra muß weder kommutativ noch assoziativ noch unitär sein.
• Der reelle Vektorraum 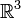$\mathbb{R}^3$ mit dem Kreuzprodukt. Diese reelle Algebra ist insbesondere eine Lie-Algebra.
• Eine Lie-Algebra ist eine Algebra, in der die beiden folgenden Bedingungen gelten (in Lie-Algebren wird das Produkt meist als [x,y] geschrieben):
  • [x,x] = 0
  • [x,[y,z]] + [y,[z,x]] + [z,[x,y]] = 0 (Jacobi-Identität)
• Eine Baric-Algebra.

Einzelnachweise

1. ↑ siehe z.B. bei Dickson (1905), http://www-groups.dcs.st-and.ac.uk/~history/Extras/Dickson_linear_algebras.html
2. ↑ siehe z.B. R. Lidl und J. Wiesenbauer, Ringtheorie und ihre Anwendungen, Wiesbaden 1980, ISBN 3-400-00371-9, Seite