Porous-Medium-Gleichung

Die Poröse-Medien-Gleichung (auch englisch als porous medium equation bezeichnet) ist eine nichtlineare degenerierte parabolische partielle Differentialgleichung. Sie besitzt die Form

$\frac{\partial u}{\partial t} = \Delta u^m$,

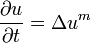worin m > 1 ist und 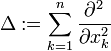$\Delta := \sum_{k=1}^n \frac{\partial^2}{\partial x_k^2}$ den räumlichen Laplace-Operator bezeichnet.

Die Poröse-Medien-Gleichung wird beispielsweise verwendet, um den Fluss eines idealen Gases in einem homogenen porösen Medium zu beschreiben. In diesem Falle ist dann die Dichte des Gases eine Lösung der Poröse-Medien-Gleichung.

Sie wird auch gelegentlich als nichtlineare Wärmeleitungsgleichung bezeichnet, da man diese bei Einsetzen von m = 1 erhalten würde. Die Wärmeleitungsgleichung besitzt jedoch unphysikalische Eigenschaften, insbesondere eine unendliche Ausbreitungsgeschwindigkeit. Durch die Degeneriertheit (m > 1) erhalten die Lösungen aber wesentlich andere Eigenschaften, nämlich beispielsweise eine endliche Ausbreitungsgeschwindigkeit (englisch: finite speed of propagation).

Literatur

• Lawrence Craig Evans: Partial Differential Equations. In: Graduate Studies in Mathematics. Band 19, American Mathematical Society, Providence, Rhode Island, 1999, ISBN 0-8218-0772-2.
• Juan Luis Vázquez: The Porous Medium Equation. In: Oxford Mathematical Monographs. Clarendon Press, Oxford 2007, ISBN 0-19-856903-3.