Gitterparameter

Ein Gitterparameter oder eine Gitterkonstante, manchmal auch Zellparameter genannt, ist entweder eine Längenangabe oder ein Winkel, der zur Beschreibung eines Gitters, insbesondere der kleinsten Einheit des Gitters, der Elementarzelle, benötigt wird. Der Gitterparameter ist entweder eine Seitenlänge der Elementarzelle oder ein Winkel zwischen den Kanten der Zelle. Gitterparameter sind bedeutend in der Kristallographie und der Optik.

Definition Gitterparameter

Die Gitterkonstanten eines dreidimensionalen Gitters

Das Gitter wird durch periodisches Verschieben einer Elementarzelle um jeweils denselben Abstand in eine bestimmte Raumrichtung (Gittervektor) erzeugt.

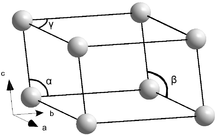
Für ein eindimensionales (optisches) Gitter genügt ein Gitterparameter, die Angabe des Abstandes benachbarter (paralleler) Gitterelemente. In zwei Dimensionen gibt es zwei verschiedene Gittervektoren und drei notwendige Gitterparameter - zwei Längen und der Winkel zwischen den Gittervektoren. Für die Beschreibung eines dreidimensionalen Gitters werden maximal sechs Parameter, drei Längen und drei Winkel benötigt. Diese sechs Parameter, die die Elementarzelle definieren, werden oft mit a, b, c und α, β, γ bezeichnet. Drei davon, die Längen a, b, und c, beschreiben den Abstand zweier Gitterebenen, die mit den Seitenflächen der Elementarzellen zusammenfallen. Die anderen drei, α, β, γ benennen die Winkel zwischen den Gittervektoren, die durch Translation der Elementarzelle die Struktur aufbauen und zwar α den Winkel zwischen b und c, β den WInkel zwischen a und c sowie γ den Winkel zwischen a und b. Die Beschreibung eines Gitters durch Gitterparameter ist nicht eindeutig. Verschiedene Sätze von Gitterparametern können dasselbe Gitter beschreiben. Daher wird in der Regel als Einheitszelle die konventionelle Zelle verwendet. Bei dieser Wahl der Einheitszelle können in den einzelnen Kristallsystemen bereits einzelne Gitterprameter festliegen, so dass die Anzahl der unabhängigen Gitterparameter verringert ist. Daher benötigt man zur Beschreibung des kubischen Gitters nur einen Gitterparameter, zur Beschreibung des tetragonalen, hexagonalen und trigonalen zwei, für das orthogonale drei, das monokline vier und das trikline sechs.

Bestimmung von Gitterparametern

Gitterparameter können im einfachsten Fall direkt oder mit dem Mikroskop gemessen werden. Beispielsweise besitzt ein Gitter mit 250 Linien pro Zentimeter eine Gitterkonstante von $g = \tfrac{1\ \mathrm{cm}}{250} = 0{,}004\ \mathrm{cm}$.

Zum direkten Vermessen der Parameter von kristallinen Stoffen können das Transmissionselektronenmikroskop oder das Rastertunnelmikroskop verwendet werden. Zumeist erfolgt die Ermittlung der Gitterparameter aber mittels Beugungsmethoden, beispielsweise mit der Röntgenbeugung. Bei der Röntgenstrukturanalyse ist die Bestimmung der Gitterparameter der erste Schritt zur Bestimmung der vollständigen Kristallstruktur.

Die Zellparameter von Oberflächenstrukturen können mit Hilfe der Beugung langsamer Elektronen (LEED, Low Energy Electron Diffraction) bestimmt werden.

Beispiele von Gitterparametern

Der Gitterparameter von Silicium, das eine Diamant-Kristallstruktur ausbildet, wurde mit sehr großer Genauigkeit gemessen und beträgt 543,102 0504 (89) pm^[1][2] Die genaue Vermessung wurde im Hinblick auf eine mögliche neue Festlegung des Kilogramms und des Mols durchgeführt.

Die Massendichte eines kristallinen Stoffs lässt sich aus den Gitterparametern bestimmen. Im einfachen Fall kubischer Gitter ist die Dichte: $\rho = n \frac{A_r \, u}{a^3}$ mit der Zahl n der Atome je Elementarzelle, der relativen Atommasse A_r, der atomaren Masseneinheit u und dem Gitterparameter a berechnen. Die Zahl n ist 8 für Diamant-Gitter, 4 für kubisch flächenzentrische Gitter, 2 für kubisch raumzentrische Gitter und eins für einfach kubische Gitter.

Die Bindungslänge im Diamant-Gitter ist $l = a \cdot \tfrac{\sqrt{3}}{4}$ , im kubisch flächenzentrischen Gitter $l = a \cdot \tfrac{\sqrt{2}}{2}$, im kubisch raumzentrischen Gitter $l = a \cdot \tfrac{\sqrt{3}}{2}$ und im einfach kubischen Gitter l = a.

Der Gitterparameter von Eisen mit einem kubisch raumzentrischen Gitter ist 286,65 pm. Für den Gitterparameter kubisch flächenzentrierter Strukturen seien die Beispiele Nickel 352,4 pm, Kupfer 361,48 pm, Silber 408,53 pm, und Gold 407,82 pm genannt.

Siehe auch

• Kristall
• Elementarzelle
• Millersche Indizes
• Optisches Gitter
• Vegardsche Regel

Einzelnachweise

1. ↑ CODATA Recommended Values. National Institute of Standards and Technology, abgerufen am 21. Juni 2011.  Gitterparameter von Silicium. Die eingeklammerten Ziffern geben die geschätzte Standardabweichung für den Mittelwert an, der den beiden letzten Ziffern vor der Klammer entspricht.
2. ↑ Die Messung der Gitterkonstante erfolgte mit Silicium natürlich vorkommender Isotopenzusammensetzung bei einer Temperatur von 22,5°C im Vakuum, vgl. S. 33 und S. 676.