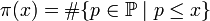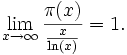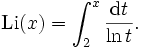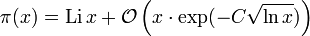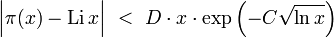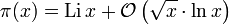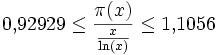- Primzahlfunktion
-
Der Primzahlsatz erlaubt eine endliche Abschätzung der Verteilung der Primzahlen. Der Zusammenhang zwischen Primzahlen und Logarithmen wurde bereits von dem 15-jährigen Carl Friedrich Gauß 1793 und unabhängig von ihm durch Adrien-Marie Legendre 1798 vermutet, aber erst 1896 unabhängig von Jacques Salomon Hadamard und Charles-Jean de La Vallée Poussin bewiesen.
Inhaltsverzeichnis
Die Primzahlfunktion
Im weiteren sei π(x) die Primzahlfunktion, die für beliebige reelle Zahlen x definiert ist als die Anzahl der Primzahlen
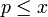 . Formal kann man schreiben:
. Formal kann man schreiben:Dabei bezeichnet das Symbol
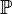 die Menge der Primzahlen, die Schreibweise
die Menge der Primzahlen, die Schreibweise 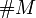 steht für die Anzahl der Elemente der Menge M.
steht für die Anzahl der Elemente der Menge M.Der Primzahlsatz
Der Primzahlsatz besagt:
Nennt man zwei reelle Funktionen f(x) und g(x) asymptotisch äquivalent, in Formelschreibweise
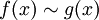 , wenn der Quotient f(x) / g(x) für
, wenn der Quotient f(x) / g(x) für 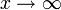 gegen 1 konvergiert, so kann man den Primzahlsatz auch so formulieren:
gegen 1 konvergiert, so kann man den Primzahlsatz auch so formulieren:- Die Funktionen π(x) und x / lnx sind asymptotisch äquivalent.
Stärkere Formen des Primzahlsatzes
Bessere Approximationen als x / lnx liefert der so genannte europäische Integrallogarithmus, der definiert wird als
(Die Integraldarstellung für Li(x) wird gewählt, weil die Stammfunktion von 1/ln(x) nicht elementar ist.)
Der Integrallogarithmus ist asymptotisch äquivalent zu x / lnx, also auch zu π(x).
Man kann sogar zeigen:
-
- mit einer positiven Konstanten C.
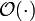 ist dabei ein Landau-Symbol, d.h., es gibt eine Konstante D, so dass
ist dabei ein Landau-Symbol, d.h., es gibt eine Konstante D, so dassfür alle x gilt.
Unter Annahme der Riemannschen Vermutung, und nur unter dieser, kann man die Fehlerabschätzung zuverbessern.
Geschichte
- Legendre veröffentlichte 1798 als erster in seiner Théorie des nombres (Abhandlung über Zahlentheorie) unabhängig den von Gauß vermuteten Zusammenhang zwischen Primzahlen und Logarithmen. In der zweiten Auflage dieses Werks 1808 verbesserte er die Abschätzung der Anzahl der Primzahlen π(x) zu ungefähr gleich
- Tschebyschow zeigte 1851 die folgende schwächere Form des Primzahlsatzes:
-
- für alle hinreichend großen x.
- In seiner berühmten Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe (1859) hat Bernhard Riemann den Zusammenhang zwischen der Verteilung der Primzahlen und den Eigenschaften der Riemannschen Zetafunktion aufgezeigt. Später wurde bewiesen, dass der Primzahlsatz dem Satz äquivalent ist, dass die riemannsche Zetafunktion keine Nullstellen mit Realteil 1 hat.
- Sowohl Hadamard als auch de la Vallée Poussin haben 1896 die Nichtexistenz solcher Nullstellen bewiesen. Ihre Beweise des Primzahlsatzes sind also nicht „elementar“, sondern verwenden funktionentheoretische Methoden.
- Lange Jahre galt ein elementarer Beweis des Primzahlsatzes für unmöglich, was 1949 durch die von Atle Selberg und Paul Erdős gefundenen Beweise widerlegt wurde (wobei „elementar“ hier keineswegs „einfach“ bedeutet). Später wurden noch zahlreiche Varianten und Vereinfachungen dieser Beweise gefunden.
Zahlenbeispiele
Die folgende Tabelle zeigt konkrete Werte des Primzahlsatzes im Vergleich mit den Logarithmen, Legendres Formel sowie dem Integrallogarithmus. x π(x) π(x) / x x / ln(x) π(x)·ln(x) / x Legendre Li(x) 10 4 0,400000 4 0,921034 8 6 102 25 0,250000 22 1,151292 28 30 103 168 0,168000 145 1,160503 172 178 104 1.229 0,122900 1.086 1,131951 1.231 1.246 105 9.592 0,095920 8.686 1,104320 9.588 9.630 106 78.498 0,078498 72.382 1,084490 78.543 78.628 107 664.579 0,066458 620.421 1,071175 665.140 664.918 108 5.761.455 0,057615 5.428.681 1,061299 5.768.004 5.762.209 109 50.847.534 0,050848 48.254.942 1,053727 50.917.519 50.849.235 1010 455.052.511 0,045505 434.294.482 1,047797 455.743.004 455.055.615 1011 4.118.054.813 0,041181 3.948.131.654 1,043039 4.124.599.869 4.118.066.401 1012 37.607.912.018 0,037608 36.191.206.825 1,039145 37.668.527.415 37.607.950.281 1013 346.065.536.839 0,034607 334.072.678.387 1,035899 346.621.096.885 346.065.645.810 1014 3.204.941.750.802 0,032049 3.102.103.442.166 1,033151 3.210.012.022.164 3.204.942.065.692 1015 29.844.570.422.669 0,029845 28.952.965.460.217 1,030795 29.890.794.226.982 29.844.571.475.288 1016 279.238.341.033.925 0,027924 271.434.051.189.532 1,028752 279.660.033.612.131 279.238.344.248.557 1017 2.623.557.157.654.233 0,026236 2.554.673.422.960.305 1,026964 2.627.410.589.445.923 2.623.557.165.610.822 1018 24.739.954.287.740.860 0,024740 24.127.471.216.847.324 1,025385 24.775.244.142.175.635 24.739.954.309.690.415 1019 234.057.667.276.344.607 0,023406 228.576.043.106.974.646 1,023982 234.381.646.366.460.804 234.057.667.376.222.382 1020 2.220.819.602.560.918.840 0,022208 2.171.472.409.516.259.138 1,022725 2.223.801.523.570.829.204 2.220.819.602.783.663.484 1021 21.127.269.486.018.731.928 0,021127 20.680.689.614.440.563.222 1,021594 21.154.786.057.670.023.133 21.127.269.486.616.126.182 1022 201.467.286.689.315.906.290 0,020147 197.406.582.683.296.285.296 1,020570 201.721.849.105.666.574.218 201.467.286.691.248.261.498 1023 1.925.320.391.606.803.968.923 0,019253 1.888.236.877.840.225.337.614 1,019639 1.927.681.221.597.738.628.080 1.925.320.391.614.054.155.139 Die Größe π(x) / x heißt Primzahldichte.
Vergleicht man Li(x) mit den Werten von π(x) in der Tabelle, scheint es so, als ob stets Li(x) > π(x) gelten würde. Tatsächlich wechselt die Differenz Li(x) − π(x) bei größer werdendem x das Vorzeichen unendlich oft, wie J. E. Littlewood 1914 zeigen konnte. Die gaußsche Formel unterschätzt also die Anzahl der Primzahlen in einem hinreichend großen Zahlenbereich, den Stanley Skewes 1933 mit der nach ihm benannten Skewes-Zahl nach oben abschätzen konnte.
Literatur
- E. Freitag, R. Busam: Funktionentheorie. 3. Aufl., Springer-Verlag, Berlin 2000. ISBN 3540676414
- G. H. Hardy, E. M. Wright, An Introduction to the Theory of Numbers, 5. Auflage, Oxford University Press, Oxford 1979. ISBN 0198531710
Weblinks
Einzelnachweise
Wikimedia Foundation.