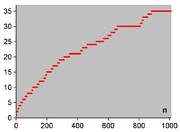
Primzahlenzwillinge

Anzahl der Primzahl-Zwillingspaare kleiner gleich n

Ein Primzahlzwilling ist ein Paar aus zwei Primzahlen, deren Abstand 2 ist. Die kleinsten Primzahlzwillinge sind (3 und 5), (5 und 7) und (11 und 13).

Geschichtliches

Der Begriff Primzahlzwilling wurde erstmals von Paul Stäckel benutzt.

Definition

Primzahlzwillinge nennt man zwei Primzahlen p₁ und p₂, deren Differenz p₂ − p₁ = 2 ist. Die Primzahl p₂ = p₁ + 2 wird dabei auch als Primzahlzwilling zur Primzahl p₁ bezeichnet.

Eigenschaften

Mit Ausnahme des Primzahlzwillings (3,5) liegt zwischen den beiden Primzahlen eines Primzahlzwillings immer eine durch 6 teilbare Zahl. Jede ganze Zahl lässt sich nämlich in der Form 6n − 2, 6n − 1, 6n, 6n + 1, 6n + 2 oder 6n + 3 darstellen, wobei n eine ganze Zahl ist. Zahlen der Form 6n − 2, 6n und 6n + 2 sind durch 2 teilbar und können deswegen mit Ausnahme der Zwei keine Primzahlen sein. Zahlen der Form 6n + 3 sind durch 3 teilbar und können deswegen mit Ausnahme der Drei auch keine Primzahlen sein. Somit haben alle Primzahlen über 3 die Form 6n − 1 oder 6n + 1. Daraus folgt, dass jeder Primzahlzwilling mit Ausnahme von (3,5) die Darstellung (6n − 1,6n + 1) hat.

Des Weiteren folgt auch

$(6n-1) \cdot (6n+1) + 1 = 36n^2 - 1 + 1 = 36n^2 = (6n)^2$.

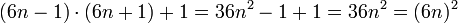n (6n-1) (6n+1) 1 5 7 2 11 13 3 17 19 5 29 31 7 41 43 10 59 61 12 71 73 17 101 103 18 107 109 23 137 139 25 149 151 30 179 181

n (6n-1) (6n+1) 32 191 193 33 197 199 38 227 229 40 239 241 45 269 271 47 281 283 52 311 313 58 347 349 70 419 421 72 431 433 77 461 463 87 521 523

n (6n-1) (6n+1) 95 569 571 100 599 601 103 617 619 107 641 643 110 659 661 135 809 811 137 821 823 138 827 829 143 857 859 147 881 883 170 1019 1021 172 1031 1033

n (6n-1) (6n+1) 175 1049 1051 177 1061 1063 182 1091 1093 192 1151 1153 205 1229 1231 213 1277 1279 215 1289 1291 217 1301 1303 220 1319 1321 238 1427 1429 242 1451 1453 247 1481 1483

n (6n-1) (6n+1) 248 1487 1489 268 1607 1609 270 1619 1621 278 1667 1669 283 1697 1699 287 1721 1723 298 1787 1789 312 1871 1873 313 1877 1879 322 1931 1933 325 1949 1951 333 1997 1999

Mit Ausnahme von n=1 ist die letzte Ziffer eines n eine 0, 2, 3, 5, 7 oder eine 8, da im anderen Fall eine der beiden Zahlen 6n-1 bzw. 6n+1 durch 5 teilbar und damit keine Primzahl wäre.

Mit einer ganzen Zahl n lässt sich jede ungerade Zahl in der Form 30n+1, 30n+3, 30n+5, 30n+7, ..., 30n+25, 30n+27, 30n+29 (letztere auch als 30n-1) darstellen. Primzahlen (außer 3 und 5) sind aber nie von einer der 7 Formen 30n+3, 30n+5, 30n+9, 30n+15, 30n+21, 30n+25 und 30n+27, da Zahlen dieser 7 Formen stets durch 3 oder durch 5 teilbar sind.

Daher hat jedes Primzahlzwillingspaar (außer (3,5) und (5,7)) mit einer ganzen Zahl n genau eine der drei Formen

(30n-1, 30n+1), (30n+11, 30n+13), (30n+17, 30n+19)

bzw. die letztere Darstellung, um die Symmetrie zu (30n+11, 30n+13) zu verdeutlichen, alternativ geschrieben als (30n-13, 30n-11).

Sonstiges

Das kleinste Paar von Primzahlzwillingen ist (3; 5).

Das größte derzeit bekannte Paar von Primzahlzwillingen ist

$2003663613 \cdot 2^{195.000} \pm1$,

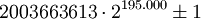das sind Zahlen mit 58.711 Ziffern. Das Zahlenpaar wurde von Twin Prime Search mit Unterstützung des DC-Projekts PrimeGrid gefunden. Der bisherige Rekord aus dem Jahr 2006 wurde damit um gut 7000 Ziffern übertroffen.

Zwei Primzahlzwillinge mit dem Abstand von vier, also Folgen der Form 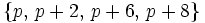$\{p,\, p+2,\, p+6,\, p+8\}$, nennt man Primzahlvierlinge.

Offene Fragestellung

Je größere Zahlen man betrachtet, desto weniger Primzahlen findet man dort. Obwohl unendlich viele Primzahlen existieren, ist es ungewiss, ob es unendlich viele Primzahlzwillinge gibt.

Zwar veröffentlichten die Mathematiker Dan Goldston und Cem Yıldırım 2003 einen Beweis, mit dem sie zeigen wollten, dass es in der unendlichen Folge der Primzahlen immer wieder kleine Abstände zwischen zwei aufeinander folgenden Primzahlen gibt, doch Andrew Granville fand noch im selben Jahr einen Fehler in dem 25-seitigen Beweis. Im Mai 2005 konnten Goldston und Yıldırım et al. eine Korrektur vorlegen. Diese wurde von den damaligen Fehlerfindern überprüft und als korrekt gewertet. Der neue, nun saubere Beweis zeigt zudem eine neue Methode auf, die es ermöglichen sollte, den endgültigen Beweis zur Anzahl der Primzahlzwillinge abzuschließen und gilt daher als großer Durchbruch.

Die Summe der Kehrwerte der Primzahlen ist divergent, jedoch hat Viggo Brun im Jahr 1919 bewiesen, dass die Summe der Kehrwerte der Primzahlzwillinge konvergiert. Aus dieser Tatsache kann man nicht schließen, ob es endlich oder unendlich viele Primzahlzwillinge gibt. Der Grenzwert der Summe wird Brunsche Konstante genannt und beträgt nach der neuesten Schätzung von 2002 etwa 1,902160583104.

Weblinks

• Die 20 größten bekannten Primzahlzwillinge