Prädikatssymbol

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite, Abschnitt "Überarbeitungsbedarf (war: Überschneidung mit Quantor)" angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Artikel Prädikatenlogik und Prädikat (Logik) überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Hafenbar 23:35, 2. Mai 2008 (CEST)

Prädikat (von lat. praedicare = zusprechen) nennt man in der Logik den Teil einer logischen Aussage - d.h. eines Satzes, der wahr oder falsch sein kann -, durch den etwas von etwas anderem ausgesagt (prädiziert), d.h. zu- oder abgesprochen wird.

Dabei wird der Ausdruck "Prädikat" vielfach sowohl für einen Ausdruck als auch für dessen Inhalt verwendet. Erst Frege führte die Trennung zwischen „Begriffsausdruck“ und „Begriff“ konsequent durch^[1]. Dies verschärft die erkenntnistheoretische Frage, ob die "prädikative Struktur von Aussagen"^[2] primär eine Eigenschaft des Denkens oder der Sprache ist^[3]. In der logischen Praxis kann dies offen bleiben.

Das Prädikat im Sinne der Logik (logisches Prädikat) ist zu unterscheiden vom Prädikat im Sinne der Grammatik (grammatisches Prädikat) (siehe: Prädikat (Grammatik)). Unter dem Einfluss der modernen Logik orientieren sich manche neuere grammatische Prädikatstheorien jedoch am logischen Prädikatsbegriff.

Das logische Prädikat wird in der modernen Logik auch als Prädikator ^[4] oder genereller Term(inus)^[5] bezeichnet, um es vom grammatischen Prädikat terminologisch abzugrenzen.

In der Logik ist zwischen dem traditionellen und dem modernen logischen Prädikatsbegriff zu unterscheiden.

• Der traditionelle Prädikatsbegriff wurde von Aristoteles begründet und herrschte bis ins 19. Jahrhundert vor. Danach ist logisches Prädikat das, von einem Subjekt ausgesagt wird.

• In der modernen Logik ist das logische Prädikat seit Frege das, was von einem oder mehreren Gegenständen ausgesagt wird.^[6]

Das Prädikat in der traditionellen Logik

In der traditionellen Logik (vor allem der Syllogistik) wird bei der Analyse von Aussagen (traditionell kategorische Urteile genannt) unterschieden zwischen dem, worüber etwas ausgesagt wird (dem Subjekt), und dem, das darüber ausgesagt wird (dem Prädikat). Das Subjekt ist der Gegenstand, über den etwas ausgesagt wird, und Prädikat das, was ihm in der Aussage zugeschrieben wird, zum Beispiel eine Eigenschaft. Der Teil der Aussage, der auf den Gegenstand verweist, ist der Subjektsterm und der Teil der Aussage, die dem Subjekt das Prädikat zuschreibt, der Prädikatsterm. Faktisch wird aber (anders als in diesem Artikel) in der Regel „Subjekt“ auch im Sinne von „Subjektsterm“ und „Prädikat“ im Sinne von „Prädikatsterm“ verwendet. Der Sprechakt der Zuschreibung selbst ist die Prädikation.

Beispiele von einfachen Aussagen sind (vgl. Wittgensteins Elementarsatz):

1. Sokrates ist ein Mensch.
2. Der Hund meines Nachbarn schläft.
3. Sokrates liebt es, bei langen Weinabenden über Philosophie zu diskutieren.

In den Beispielen 1 und 3 ist der Mensch Sokrates das Subjekt, der Ausdruck „Sokrates“ (der erste Teil der Aussagen 1 und 3) der Subjektsterm. Im Beispiel 2 ist der Hund meines Nachbarn (das Tier, das mich jeden morgen anbellt) das Subjekt und der Ausdruck „Der Hund meines Nachbarn“ der Subjektsterm.

Beispiel 2 zeigt, dass grammatisches Subjekt („Der Hund“) und logisches Subjekt (genauer: Subjektsterm) nicht übereinstimmen müssen: Grammatisch ist „meines Nachbarn“ ein konstitutives Attribut zum Subjekt.

Die Prädikate in den Beispielsätzen sind die Eigenschaften ein Mensch zu sein, zu schlafen und es zu lieben, bei langen Weinabenden über Philosophie zu diskutieren. Die Prädikatsterme sind „Mensch“, „schläft“ und „liebt es, bei langen Weinabenden über Philosophie zu diskutieren“.

Das erste und letzte Beispiel zeigen, dass das logische Prädikat (genauer: der Prädikatsterm) nicht mit dem grammatischen Prädikat („ist“ bzw. „liebt“) übereinstimmen muss: Grammatisch ist „ein Mensch“ ein Gleichsetzungsnominativ, „bei langen Weinabenden über Philosophie zu diskutieren“ ein Akkusativobjekt.

Als Teile einer einfachen Aussage sind Prädikatsterm und Subjektsterm unvollständig und selbst keine Aussagen. Sie können nicht für sich wahr oder falsch sein.

Im Beispiel 1 ist der Prädikatsterm aus zwei Teilen zusammengesetzt: der Kopula „ist“ und dem Prädikatsnomen „der Mensch“. In der Syllogistik hat es sich eingebürgert, auch die Prädikate in Beispielen 2 und 3 in dieser Form zu schreiben, weil sie nur dann im Rahmen des formalen, syllogistischen Schließens unmittelbar verwendbar sind. Also etwa:

• Der Hund meines Nachbarn ist ein Schlafender.
• Sokrates ist ein Liebender des Diskutierens über Philosophie bei langen Weinabenden.

Unter Zugrundelegung des traditionellen Subjekts- und Prädikatsbegriffs unterscheidet Immanuel Kant zwischen analytischen Urteilen, bei denen das Prädikat bereits im Subjekt enthalten sei (z. B. bei der Aussage „Alle Kreise sind rund“) und synthetischen Urteilen, bei denen das Prädikat dem Subjekt etwas hinzufüge (z. B bei der Aussage „Der Hund schläft“). Zu dieser kantischen Unterscheidung siehe Synthetisches Urteil a priori.

Der moderne Prädikatsbegriff

Begriff

Ein Prädikat im Sinne der modernen Logik ist "ein Ausdruck, aus dem man durch Einsetzen von Individuennamen für Individuenvariablen einen Satz bilden kann."^[7].

Anders gewendet: Ein Prädikat ist der Ausdruck, der übrigbleibt, wenn man in einem Satz die in ihm vorkommenden Namen wegstreicht^[8].

Grundlegend für den modernen Prädikatsbegriff ist die Einsicht von Frege, dass der beurteilbare Inhalt einer Aussage ein Ganzes ist, "das logisch auf verschiedene Weise zerlegt werden kann, jedoch immer so, dass von einem Gegenstand Beziehungen oder Eigenschaften ausgesagt werden."^[9]. In Anwendung und Erweiterung des Funktionsbegriffs der Analysis wird die Aussage nicht mehr in Subjekt und Prädikat, sondern in Funktion und Argument zerlegt^[10]. Das Subjekt-Prädikat-Schema der Umgangssprache wird für die Logik durch ein Argument-Funktion-Schema ersetzt^[11]. Dabei vertritt das Argument einen Gegenstand, von dem bestimmte Eigenschaften oder Beziehungen gelten, die durch eine Funktion (d.h. ein logisches Prädikat) ausgedrückt werden.^[12]

Prädikate als Satzfunktionen

Das Prädikat im Sinne der modernen Logik ist eine Satzfunktion, die auch als Aussagefunktion, Aussageform oder (engl.) propositional function bezeichnet wird. Von jeder Satzfunktion wird gefordert, dass sie für jedes Argument (jeden singulären Ausdruck), das man in sie einsetzt, einen Wahrheitswert ergibt.

In treffender Formulierung heißt es: „n-stellige Prädikate sind eigentlich n-stellige Funktionen, deren Funktionswerte nichts mit Zahlen zu tun haben. Vielmehr geben sie Wahrheitswerte. Einstellige Prädikate nehmen als Argumente einzelne Gegenstände und geben Wahrheitswerte. Zweistellige Prädikate nehmen als Argumente geordnete Paare von Gegenständen und geben Wahrheitswerte ... kurz: n-stellige Prädikate nehmen n-Tupel als Argumente und geben Wahrheitswerte.“^[13] Die Extension eines n-stelligen Prädikats ist dabei die Menge der n-Tupel, für die das Prädikat den Wahrheitswert "wahr" ergibt^[14].

Es gibt zwei Möglichkeiten, aus Prädikaten Sätze (d.h. Aussagesätze) zu gewinnen: (1) zum einen dadurch, dass man das Prädikat „auf bestimmte einzelne Gegenstände oder auf bestimmte n-Tupel von Gegenständen anwendet, oder (2) dadurch, dass man das Prädikat „auf den Gegenstandsbereich oder eine seiner Produktmengen anwendet“^[15], d.h. dadurch, dass man die Variablen (bzw. Leerstellen) durch Individuennamen ersetzt oder durch Quantifizierung bindet.

Prädikate, Relationen und Existenzaussagen

Der moderne Prädikatsbegriff macht den Weg frei, auch Beziehungen (Relationen) sowie Existenzaussagen logisch adäquat zu erfassen.

Prädikate und Relationen

Der moderne Prädikatsbegriff ermöglicht eine Mehrstelligkeit des Prädikats und dadurch eine logische Behandlung von Relationen.

• Beispiel: „Sokrates ist ein Schüler von Platon“

traditionelle Analyse: "Sokrates" (Subjekt) "ist" (Kopula) "ein Schüler von Platon" (Prädikat)

moderne Analyse: Die Beziehung des „Schülerseins von“ wird als Prädikatsterm „_₁ ist Schüler von _₂“ analysiert; die Ausdrücke „_₁“ und „_₂“ markieren dabei die Stellen, an denen die Individuen benannt werden, über die diese Beziehung ausgesagt werden soll – im Beispiel sind das die Individuen (Argumente, Gegenstände) Sokrates und Platon.

Im Fall von „_₁ ist Schüler von _₂“ handelt es sich um eine Beziehung zwischen zwei Gegenständen, weshalb das Prädikat (bzw. der Prädikatsterm) zweistellig genannt wird. Abhängig von der Zahl der Gegenstände zwischen denen eine Beziehung ausgesagt wird, spricht man auch von drei-, vier-, usw. stelligen Prädikaten, oder allgemeiner von n- oder unbestimmt mehrstelligen.

Prädikate und Existenzaussagen

Der moderne Prädikatsbegriff ermöglicht auch Existenzaussagen adäquater zu erfassen.

• Beispiel: (1) "Es gibt violette Ameisen"; (2) „Einige Ameisen sind violett“; (3) „Violette Ameisen existieren“^[16]

traditionelle Logik: Bei (1) ist "Es" grammatisch ein Schein-Subjekt, was für die traditionelle Logik ein Problem darstellt. Formuliert man (1) und (3) in "Violette Ameisen sind existierend" um, kann man diesen Satz in "Violette Ameisen" (Subjekt) + "sind" (Kopula) und "existierend" (Prädikat) analysieren. Dieser Satz unterscheidet sich von (2): "Einige Ameisen" (Subjekt) + "sind" (Kopula) + "violett" (Prädikat).

moderne Logik: Für die moderne Logik sind die Sätze (1) - (3) gleichbedeutend und "existieren" ist nur in einem grammatischen, nicht aber in einem logischen Sinn ein Prädikat.^[17]. Die Einzelheiten sind umstritten. Nach Frege ist Existenz die Eigenschaft eines Begriffs, einen nicht-leeren Umfang zu haben^[18]. Als locus classicus für die moderne Auffassung von Existenz gilt Russells Aufsatz „On Denoting“ (1905).^[19]

Begriffe als Bedeutungen von Prädikaten

Sieht man mit Frege in Prädikaten Satzfunktionen, verwendet man den Ausdruck "Begriff" mit ihm in einem nur logischen Sinn^[20] und sieht man in Begriffen die Bedeutung von Prädikaten^[21], so kommt man zu seiner klassischen Begriffsdefinition: „ein Begriff ist eine Funktion, deren Wert immer ein Wahrheitswert ist“^[22].

Dies gilt als „der erste standfeste Begriff des Begriffs in der europäischen Philosophiegeschichte“^[23].

Prädikate als Namen für Eigenschaften und Relationen

Zwischen den Prädikaten als sprachlichen Ausdrücken und ihren Bedeutungen ist streng zu unterscheiden^[24].

So bedeutet z.B. das Prädikat "ist weiß" die Eigenschaft, weiß zu sein, und das Prädikat "Freund sein" die Beziehung der Freundschaft^[25].

Die Bedeutung n-stelliger Prädikate bezeichnet man auch als n-stellige Begriffe^[26].

Prädikate sind "Bezeichnungen für Eigenschaften und Relationen, die von den Individuen ausgesagt werden sollen"^[27]. Einstellige Prädikate sind "ein Zeichen für ein einstelliges Attribut (d.i. eine Eigenschaft)“ ^[28]. Je nach relationslogischer Terminologie kann man n-stellige Prädikate auch als einstellige Beziehungsausdrücke bezeichnen^[29].

Prädikatsbegriff und Ontologie

Vereinzelt wird davor gewarnt, den Ausdruck Prädikat mit den Ausdrücken „Eigenschaft“ oder „Beziehung“ in Zusammenhang zu bringen, da dies zu „ontologisch-philosophischen Problemen“ führe^[30].

Für den aristotelischen Prädikatsbegriff heißt es resümierend: "Die Relation von Subjekt und Prädikat im Satz spiegelt das Grundverhältnis der Wirklichkeit: die Substanz (Subjekt) mit ihren Eigenschaften (Prädikate). Jedes wahre Urteil spiegelt ein Seinsverhältnis."^[31]

Es ist hier nicht zu vertiefen, inwieweit die klassische Ontologie mit ihrem Substanz- und Akzidenz-Denken den klassischen Prädikatsbegriff notwendig hat.

Einteilungen der Prädikate

Einstellige und mehrstellige Prädikate

Nach der Anzahl der einsetzbaren Individuennamen (Argumente) kann zwischen ein- und mehrstellige Prädikaten unterschieden werden.

Ein Prädikat mit n Leerstellen nennt man n-stelliges Prädikat.^[32]

Statt von ein-, zwei- oder dreistelligen Prädikaten wird auch von monadischen, dyadischen, triadischen Prädikaten (Prädikatoren) gesprochen.

Mehrstellige Prädikate (Prädikatoren) werden mitunter auch Relatoren" genannt.^[33]

Ein Wort kann Ausdruck von Prädikaten verschiedener Stellenzahl sein.^[34]

• Beispiel (liegen)^[35]:

• • (1) einstellig (f (a)): „Anton liegt“ (= ".. liegt" ("Anton"));

• • (2) zweistellig (f (a,b)): Anton liegt unter einer Eiche (= ".. liegt unter .." ("Anton", "Eiche").

• • (3) dreistellig (f (a, b, c)): Anton liegt zwischen einer Eiche und einer Birke (= ".. liegt zwischen .. und .." ("Anton", "Eiche", "Birke")

"Im übrigen steckt in jedem mehrsteligen Prädikat auch ein solches mit weniger Leerstellen und immer ein einstelliges."^[36]

Die Leerstellen des Prädikats entsprechen in anderer Terminologie seiner syntaktischen Valenz. ^[37]

Atomare / molekulare Prädikate

Ein atomares Prädikat (semantischer Baustein; semantisches Primitiv; engl.: semantic primitive^[38]) ist ein Prädikat, das keine Junktoren enthält^[39].

Ein molekulares Prädikat ist ein "Prädikat, das durch die Verbindung mehrerer atomarer Prädikate durch Junktoren entstanden ist"^[40].

Prädikate als Ausdrücke von Eigenschaften und Beziehungen

Einstellige Prädikate sind Ausdrücke für Eigenschaften und mehrstellige Prädikate Ausdrücke für Beziehungen - wenn man terminologisch Eigenschaften nicht als einstellige Beziehungen auffasst.

Im Einzelnen siehe schon oben.

Prädikate erster und zweiter Stufe

Prädikate erster Stufe sind "Prädikate, deren Argumentausdrücke Individuenzeichen sind"^[41]

Prädikate zweiter Stufe sind Prädikate, deren "Argumentausdrücke Prädikate erster Stufe sind^[42]

Von Carnap werden die Individuenzeichen als Zeichen nullter Stufe bezeichnet^[43]

Leeres/ nichtleeres Prädikat

„Ein Prädikat heißt leer, wenn es auf kein Individuum zutrifft.“^[44] (Beispiel: Einhorn). Das Gegenteil ist ein nichtleeres Prädikat.

Die Formalisierung des Prädikats in der mathematischen Logik

Anders als die traditionelle Syllogistik untersucht die moderne mathematische Logik nicht das logische Schließen mit Hilfe normalsprachiger Sätze, sondern das Schließen in genau beschriebenen formalen Sprachen beziehungsweise Systemen. Für Prädikatenkalküle gehören zu den beschriebenen Ausdrücken der Sprache ein- und mehrstellige Prädikatensymbole, auch Prädikatenkonstanten, Prädikatbuchstaben oder Prädikatoren genannt, oft geschrieben als Großbuchstaben, gefolgt von den Argumenten des Prädikats oder von Leerstellen als Platzhalter für solche Argumente. Oft werden die Argumente in Klammern gesetzt und durch Beistriche voneinander getrennt. Zum Beispiel würde ein einstelliges Prädikat mit dem Prädikatensymbol „P“ als „P_“ oder als „P(_)“ geschrieben, ein zweistelliges Prädikat mit dem Prädikatensymbol „S“ würde als „S_₁_₂“ oder als „S(_₁, _₂)“ geschrieben. Die einstelligen Prädikatensymbole entsprechen den Prädikatstermen der syllogistischen Logik.

In der Interpretation einer formalen Sprache eines Prädikatenkalküls wird jedem einstelligen Prädikatensymbol die Menge der Individuen (Gegenstände, Entitäten im weitesten Sinn) zugeordnet, auf die das betroffene Prädikat zutrifft; jedem zweistelligen Prädikatensymbol die Menge geordneter Paare von Individuen, auf die das Prädikat zutrifft; und allgemein jedem n-stelligen Prädikatensymbol die Menge aller n-Tupel (in der Mathematik auch als Relation bezeichnet) von Individuen, auf die das jeweilige Prädikat zutrifft. Die Gesamtheit aller Gegenstände, von denen in der betrachteten Interpretation die Rede ist, wird Diskursuniversum (engl. universe of discourse oder domain) genannt.

Der Begriff Prädikat wird formal als eine Funktion in die Menge der Wahrheitswerte definiert: Ein n-stelliges Prädikat ist eine n-stellige Funktion aus dem n-fachen kartesischen Produkt des Diskursuniversums D 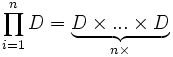$\prod_{i=1}^n D = \underbrace {D \times ... \times D}_{n \times}$ – das heißt aus der Menge aller n-Tupel von Individuen – in die Menge der Wahrheitswerte. Somit kann jedem n-stelligen Prädikatensymbol P(_₁, _₂,... __n) eine solche Funktion – ein Prädikat – P(x₁, x₂,... x_n) zugeordnet werden, sodass P(x₁, x₂,... x_n) =wahr  genau dann, wenn das n-Tupel (x₁, x₂,... x_n) ein Element der dem Prädikatensymbol zugeordneten Menge von n-Tupeln ist, mit anderen Worten:

Für alle x₁, x₂,... x_n ∈ D gilt:

(x₁, x₂,... x_n) ∈ P ⇔ P(x₁, x₂,... x_n) = Wahr

Aus diesem Grund werden die Aussagen (x₁, x₂,... x_n) ∈ P und P(x₁, x₂,... x_n) auch gleichbedeutend verwendet.

Als einfaches Beispiel eine Dreiecksgeschichte. Das universe of discourse U besteht aus Ulrich, Heiner und Anna:

U = {Ulrich, Heiner, Anna}

Wir haben zwei Prädikatssymbole "F( )" (einstellig) und "L( , )" (zweistellig). Wir ordnen das Prädikatensymbol "F( )" der einstelligen Relation (d.h. einer Teilmenge von U) {Anna} zu. Das Prädikatensymbol "L( , )" der zweistelligen Relation {(Anna, Heiner), (Heiner, Anna), (Ulrich, Anna)}. Unsere Prädikate sind F(x) und L(x₁, x₂). F(x) ist genau dann wahr, wenn x = Anna. In unserer Interpretation gilt also: F(Anna).

Einzelnachweise

1. ↑ Mayer, Der Wert der Gedanken (1989), S. 40 f. Fn. 25
2. ↑ Hoyningen-Huene, Logik (1998), S. 171
3. ↑ Hoyningen-Huene, Logik (1998), S. 171
4. ↑ z.B. von Menne, Logik, 6. Aufl. (2001), S.58; Seiffert, Logik (1973), S. 23
5. ↑ So Quine nach Tugendhat/Wolf, Logisch-semantische Propädeutik (1983), S. 94
6. ↑ Vgl. Ruppen, Einstieg in die formale Logik (1996), S. 157: "Ein Prädikat ist ein Ausdruck, den wir von einem oder mehreren Gegenständen aussagen."
7. ↑ E. von Savigny, Grundkurs im logischen Schließen, 2. Aufl. (1984), S. 85
8. ↑ Vgl. (für den einfachen Satz) Kutschera/Breitkopf, Einführung in die moderne Logik, 8. Aufl. (2007), ISBN 978-3-495-482711, S. 84
9. ↑ Mayer, Der Wert der Gedanken (1989), S. 70
10. ↑ Mayer, Der Wert der Gedanken (1989), S. 68
11. ↑ Frege, Vorwort zu Begriffsschrift, in: Meixner, (Hrsg.), Philosophie der Logik (2003), S. 27 (31)
12. ↑ Mayer, Der Wert der Gedanken (1989), S. 70
13. ↑ Strobach, Einführung in die Logik (2005), S. 83
14. ↑ Vgl. Strobach, Einführung in die Logik (2005), S. 83
15. ↑ Czayka, Logik (1991), S. 36
16. ↑ Beispiel nach Tugendhat/Wolf, Logisch-semantische Propädeutik (1983), S. 94
17. ↑ Tugendhat/Wolf, Logisch-semantische Propädeutik (1983), S. 185
18. ↑ Tatievskaya, Aussagenlogik (2003), S. 48 („vermutlich“)
19. ↑ Tugendhat/Wolf, Logisch-semantische Propädeutik (1983), S. 191 ff.
20. ↑ Vgl. R. Haller, „Begriff“, in: HWPH Bd. 1 (1971), Sp. 780 (785)
21. ↑ Mayer, Der Wert der Gedanken (1989), S. 10; ebenso Kutschera/Breitkopf, Einführung in die moderne Logik, 8. Aufl. (2007), ISBN 978-3-495-482711, S. 85
22. ↑ Frege, Funktion und Begriff [1891], in: Meixner, (Hrsg.), Philosophie der Logik [2003], S. 32 (43)
23. ↑ So Patzig, Sprache und Logik, 2. Aufl. (1981), S. 97
24. ↑ Kutschera/Breitkopf, Einführung in die moderne Logik, 8. Aufl. (2007), ISBN 978-3-495-482711, S. 85
25. ↑ Vgl. Kutschera/Breitkopf, Einführung in die moderne Logik, 8. Aufl. (2007), ISBN 978-3-495-482711, S. 85
26. ↑ Kutschera/Breitkopf, Einführung in die moderne Logik, 8. Aufl. (2007), ISBN 978-3-495-482711, S. 85
27. ↑ Carnap, Einführung in die symbolische Logik, 3. Aufl. (1968), S. 4
28. ↑ Carnap, Einführung in die symbolische Logik, 3. Aufl. (1968), S. 5
29. ↑ So z.B. Essler/Martínez, Grundzüge der Logik I, 4. Aufl. (1991), S. 174
30. ↑ Czayka, Logik (1991), S. 32 Fn. 47
31. ↑ Brandt/Dietrich/Schön, Sprachwissenschaft, 2. Aufl. (2006), S. 49
32. ↑ Kutschera/Breitkopf, Einführung in die moderne Logik, 8. Aufl. (2007), ISBN 978-3-495-482711, S. 85
33. ↑ Seiffert, Logik (1973), S. 28
34. ↑ Hoyningen-Huene, Logik (1998), S. 173
35. ↑ vgl. Hoyningen-Huene, Logik (1998), S. 173
36. ↑ Hilbert/Ackermann, Grundzüge der theoretischen Logik, 6. Aufl., Berlin u.a.. (1972), ISBN 3-540-05843-5, S. 69
37. ↑ So Bußmann, Lexikon der Sprachwissenschaft, 3. Aufl. (2002)/Argument
38. ↑ Bußmann, Lexikon der Sprachwissenschaft, 3. Aufl. (2002)/Atomares Prädikat
39. ↑ Czayka, Logik (1991), S. 36
40. ↑ Herberger/Simon, Wissenschaftstheorie für Juristen, S. 94
41. ↑ Carnap, Einführung in die symbolische Logik, 3. Aufl. (1968), S. 66; vgl. auch Menne, Logik, 6. Aufl. (2001), S. 68: „Prädikatoren 1. Stufe“ = „Prädikatoren, die Individuen als Argumente haben“
42. ↑ Carnap, Einführung in die symbolische Logik, 3. Aufl. (1968), S. 65 f.; Menne, Logik, 6. Aufl. (2001), S. 68
43. ↑ Carnap, Einführung in die symbolische Logik, 3. Aufl. (1968), S. 66
44. ↑ Menne, Logik, 6. Aufl. (2001), S. 61

Siehe auch

Prädikation