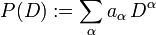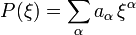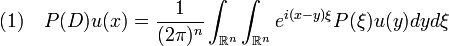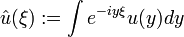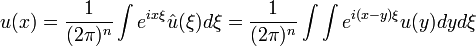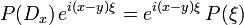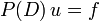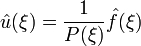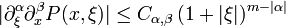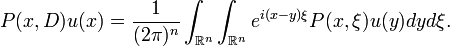Pseudo-Differentialoperator

Ein Pseudo-Differentialoperator ist eine Erweiterung des Konzepts des Differentialoperators. Sie sind ein wichtiger Bestandteil der Theorie der partiellen Differentialgleichungen. Die Grundlagen der Theorie stammen von Lars Hörmander.

Motivation

Lineare Differentialoperatoren mit konstanten Koeffizienten

Man betrachte den linearen Differentialoperator mit konstanten Koeffizienten

$P(D) := \sum_\alpha a_\alpha \, D^\alpha$

der auf dem Raum der glatten Funktionen mit kompaktem Träger (Definitionsbereich, englisch compact support) in $\mathbb{R}^n$ operiert. Er kann als Komposition einer Fouriertransformation, einer einfachen Multiplikation mit dem Polynom (dem sogenannten Symbol)

$P(\xi) = \sum_\alpha a_\alpha \, \xi^\alpha$

und der inversen Fouriertransformation:

$(1) \quad P(D) u (x) = \frac{1}{(2 \pi)^n} \int_{\mathbb{R}^n} \int_{\mathbb{R}^n} e^{i (x - y) \xi} P(\xi) u(y) dy d\xi$

geschrieben werden. Dabei ist

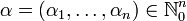$\alpha = (\alpha_1,\dots, \alpha_n) \in \mathbb{N}_0^n$ ein Multiindex, 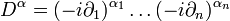$D^\alpha = (-i \partial_1)^{\alpha_1} \dots (-i \partial_n)^{\alpha_n}$ ein Differentialoperator, 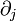$\partial_j$ steht für Ableitung nach der j-ten Variable und 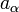$a_\alpha \,$ sind komplexe Zahlen.

Analog ist ein Pseudo-Differentialoperator P(x,D) auf $\mathbb{R}^n$ ein Operator der Form

$(2) \quad P(x,D) u (x) = \frac{1}{(2 \pi)^n} \int_{\mathbb{R}^n} \int_{\mathbb{R}^n} e^{i (x - y) \xi} P(x,\xi) u(y) dy d\xi$,

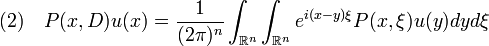mit einer allgemeineren Funktion P im Integranden, wie unten weiter ausgeführt wird.

Herleitung von Formel (1)

Die Fouriertransformation einer glatten Funktion u, mit kompaktem Träger in $\mathbb{R}^n$, ist

$\hat u (\xi) := \int e^{- i y \xi} u(y) dy$

und umgekehrte Fouriertransformation ergibt

$u (x) = \frac{1}{(2 \pi)^n} \int e^{i x \xi} \hat u (\xi) d\xi = \frac{1}{(2 \pi)^n} \int \int e^{i (x - y) \xi} u (y) dy d\xi$

Wendet man P(D) auf diese Darstellung von u an und benutzt

$P(D_x) \, e^{i (x - y) \xi} = e^{i (x - y) \xi} \, P(\xi)$

erhält man (1).

Darstellung von Lösungen von partiellen Differentialgleichungen

Um eine partielle Differentialgleichung

$P(D) \, u = f$

zu lösen werden beide Seiten (formal) fouriertransformiert, wobei sich algebraische Gleichungen ergeben:

$P(\xi) \, \hat u (\xi) = \hat f(\xi)$.

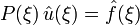Falls das Symbol P(ξ) immer ungleich Null ist für 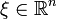$\xi \in \mathbb{R}^n$, kann man durch P(ξ):

dividieren:

$\hat u(\xi) = \frac{1}{P(\xi)} \hat f(\xi)$

Die Lösung lautet dann mit Anwendung der umgekehrten Fouriertransformation:

$u (x) = \frac{1}{(2 \pi)^n} \int e^{i x \xi} \frac{1}{P(\xi)} \hat f (\xi) d\xi$.

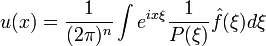Dabei wurden folgende Voraussetzungen gemacht:

1. P(D) ist ein linearer Differentialoperator mit konstanten Koeffizienten,
2. sein Symbol P(ξ) ist niemals Null,
3. sowohl u als auch f haben wohldefinierte Fouriertransformierte.

Die letzte Annahme kann mit der Theorie der Distributionen abgeschwächt werden. Die ersten beiden Annahmen können wie folgt abgeschwächt werden:

Man setze in der letzten Formel die Fouriertransformation von f ein:

$u (x) = \frac{1}{(2 \pi)^n} \int \int e^{i (x-y) \xi} \frac{1}{P(\xi)} f (y) dy d\xi$.

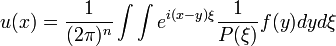Das ist ähnlich Formel (1), nur dass 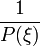$\frac{1}{P(\xi)}$ kein Polynom ist, sondern eine Funktion allgemeinerer Art.

Formale Definitionen

Symbol-Klassen

Ist P(x,ξ) eine unendlich oft differenzierbare Funktion auf 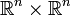$\mathbb{R}^n \times \mathbb{R}^n$ mit

$|\partial_\xi^\alpha \partial_x^\beta P(x,\xi)| \leq C_{\alpha,\beta} \, (1 + |\xi|)^{m - |\alpha|}$

für alle x,ξ, alle Multiindices α,β, eine Konstante C_α,β und reelle Zahlen m, so gehört P zur Symbolklasse $S^m_{1,0}$.

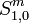Pseudo-Differentialoperatoren

Sei wieder P eine glatte Funktion aus der Symbolklasse 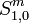$S^m_{1,0}$. Ein Pseudo-Differentialoperator der Ordnung m wird dann definiert durch

$P(x,D) u (x) = \frac{1}{(2 \pi)^n} \int_{\mathbb{R}^n} \int_{\mathbb{R}^n} e^{i (x - y) \xi} P(x,\xi) u(y) dy d\xi.$

Die Menge der Pseudo-Differentialoperator der Ordnung m wird mit 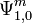$\Psi^m_{1,0}$ bezeichnet.

Eigenschaften

Lineare Differentialoperatoren der Ordnung m mit glatt beschränkten Koeffizienten sind Pseudo-Differentialoperatoren der Ordnung m.

Pseudo-Differentialoperatoren bilden den Schwartz-Raum 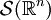$\mathcal{S}(\R^n)$ in sich ab, daher ist die Komposition PQ zweier Pseudo-Differentialoperatoren P, Q wieder ein Pseudo-Differentialoperator. Das Symbol von PQ kann aus dem von P und Q berechnet werden. Die Adjungierte und Transponierte eines Pseudo-Differentialoperators ist ebenfalls wieder ein Pseudodifferentialoperator.

Falls ein Differentialoperator der Ordnung m (gleichmäßig) elliptisch (von der Ordnung m) und invertierbar ist, ist sein Inverses ein Pseudodifferentialoperator der Ordnung -m, und sein Symbol kann berechnet werden. Man kann also lineare elliptische Differentialgleichungen mehr oder weniger explizit mit Hilfe der Theorie der Pseudodifferentialoperatoren lösen.

Differentialoperatoren sind lokal in dem Sinne, dass man nur den Wert einer Funktion in der Umgebung eines Punktes zu kennen braucht, um die Wirkung des Operators zu bestimmen. Pseudo-Differentialoperatoren sind pseudo-lokal, was grob gesagt bedeutet, dass sie auf eine Distribution angewandt keine Singularitäten an Punkten erzeugen, an denen die Distribution stetig ist.

Genauso wie ein Differentialoperator durch die D = -i * d/dx in der Form

p(x, D)

für ein Polynom p in D, genannt Symbol, ausgedrückt werden kann, hat ein Pseudodifferentialoperator ein Symbol aus einer allgemeineren Klasse von Funktionen. Häufig kann man ein analytisches Problem in der Theorie der Pseudo-Differentialoperatoren auf ein algebraisches Problem in den Symbolen reduzieren. Das ist das Wesen der mikrolokalen Analysis (microlocal analysis).

Literatur

• Michael E. Taylor, Pseudodifferential Operators, Princeton Univ. Press 1981, ISBN 0-691-08282-0
• ders. Partial differential equations, Bd. 1,2, Springer 1996, 1997, Bd.1 ISBN 0387946535, Bd.2 ISBN 0387946519
• M. A. Shubin Pseudodifferential Operators and Spectral Theory, Springer-Verlag 2001. ISBN 3-540-41195-X
• Francois Treves Introduction to Pseudo Differential and Fourier Integral Operators, Plenum 1981. ISBN 0-306-40404-4
• F. G. Friedlander, M. Joshi Introduction to the Theory of Distributions, Cambridge University Press 1999. ISBN 0-521-64971-4
• José García-Cuerva Fourier Analysis and Partial Differential Equations, CRC Press 1995. ISBN 084937877X

Weblink

• Mark Joshi, Vorlesungen über Pseudodifferentialoperatoren, englisch

• Jörg Seiler, Skriptum zu einer Vorlesung über Pseudodifferentialoperatoren