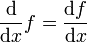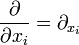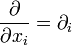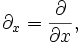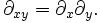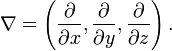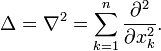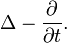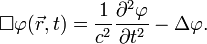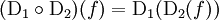Differenzialoperator

Ein Differentialoperator ist in der Mathematik eine Abbildung, die einer Funktion eine Funktion zuordnet und die Ableitung nach einer oder mehreren Variablen enthält. So ist d / dx in

${\mathrm d \over \mathrm d x}f={ \mathrm d f \over \mathrm d x}$

ein Differentialoperator. Differentialoperatoren lassen sich miteinander verknüpfen. Durch Weglassen der Funktion, auf die sie wirken, erhält man auf diese Weise reine Operatorgleichungen (Operatorkalkül).

Aus der Sicht der Mathematik führt das Studium der Differentialoperatoren zur Verallgemeinerung der Ableitung durch die schwache Ableitung und damit letztendlich zur Konstruktion von Sobolevräumen. Damit sind Ableitungen als Sonderfälle in die umfangreichere Welt der Linearen Operatoren eingebettet.

Eine Erweiterung des Konzepts ist der Begriff des Pseudo-Differentialoperators.

Notation

Neben den ausführlichen Schreibweisen

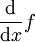$\frac{\mathrm{d}}{\mathrm{d}x}f$ (totale Ableitung nach $x\,$)

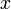bzw.

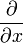$\frac{\partial}{\partial x}$ (partielle Ableitung nach $x\,$)

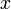haben sich weitere Schreibweisen eingebürgert, die insbesondere in der Theoretischen Physik in Verbindung mit der Einsteinschen Summenkonvention gerne verwendet werden. So wird oft äquivalent verwendet

$\frac{\partial}{\partial x_i}=\partial_{x_i}$

und, falls aus dem Kontext ersichtlich,

$\frac{\partial}{\partial x_i}=\partial_{i}$

Es ist anzumerken, dass eine gewisse Verwechslungsgefahr bezüglich des Zeichens '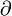$\partial$' besteht, da es neben der Verwendung als Differentialoperator auch als Randoperator verwendet wird.

Beispiele aus der Theorie partieller Differentialgleichungen

Differentialoperatoren der partiellen Ableitung einer Funktion nach einer von mehreren Variablen, beispielsweise

$\partial_x={\partial \over \partial x},$

sowie Kombinationen, wie beispielsweise

$\partial_{xy}=\partial_x\partial_y.$

Der Nabla-Operator $\nabla$ aus der Vektoranalysis, manchmal auch als $\vec\nabla$ geschrieben. Er hat für den dreidimensionalen Fall mit kartesischen Koordinaten die Gestalt des formalen Vektors

$\nabla = \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right).$

Er wird für die Formulierung des Gradienten, der Divergenz und der Rotation verwendet.

Der Laplace-Operator oder Deltaoperator

$\Delta=\nabla^2= \sum_{k=1}^n {\partial^2\over \partial x_k^2}.$

Er ist das einfachste Beispiel eines elliptischen Differentialoperators, was sich auf die Vorzeichen und die Struktur der - da die Differentialgleichung 2.Ordnung ist - quadratischen Form nach Fouriertransformation der Gleichung bezieht (ebenso wie die Begriffe hyperbolisch, parabolisch, siehe unten).

Der der Wärmeleitungs- oder Diffusionsgleichung entsprechende Operator

$\Delta - \frac{\partial}{\partial t}.$

Er ist ein Beispiel eines Operators vom parabolischen Typ.

Der d’Alembertoperator auch Quabla genannt

$\Box\varphi(\vec r, t)=\frac{1}{c^2}\frac{\partial^2\varphi}{\partial t^2}-\Delta\varphi.$

wobei c einer Geschwindigkeit entspricht. Er ist das einfachste Beispiel für eine Wellengleichung und von hyperbolischem Typ.

Lineare Differentialoperatoren

Alle oben angegebenen Beispiele von Differentialoperatoren D sind linear, das heißt es gilt

$\mathrm{D}\,(f+g) = (\mathrm{D}f) + (\mathrm{D}g)$

$\mathrm{D}\,(cf) = c\,(\mathrm{D}f)$.

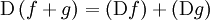
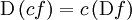mit Funktionen f, g und Konstanten c.

Viele in der Physik wichtige Differentialoperatoren wie z.B. die Schrödingergleichung in der Quantenmechanik sind linear, so dass ihre Lösungen Vektorräume bilden. Nach Fouriertransformation lassen sie sich häufig auf algebraische Gleichungen und Konzepte der linearen Algebra zurückführen. Nichtlineare Differentialoperatoren sind wesentlich schwieriger zu behandeln.

Algebra der Differentialoperatoren

Die Kombination von Differentialoperatoren lässt sich

$(\mathrm{D}_1\circ \mathrm{D}_2)(f) = \mathrm{D}_1(\mathrm{D}_2(f))$

schreiben. Damit ist eine Multiplikation der Differentialoperatoren erklärt, die mit dieser Operation und der üblichen Addition einen Ring bilden. Die Multiplikation ist aber im Allgemeinen nicht mehr kommutativ. Eine Ausnahme sind beispielsweise Differentialoperatoren mit konstanten Koeffizienten, wo die Kommutativität aus der Vertauschbarkeit der partiellen Ableitungen folgt. Man kann auch formal Potenzreihen mit den Differentialoperatoren D bilden und darüber z.B. Exponentialfunktionen exp(D). Für das Rechnen mit solchen Exponentialausdrücken von linearen Operatoren gelten die Baker-Campbell-Hausdorff-Formeln.

Symbol eines Differentialoperators

Die in den Beispielen angegebenen Differentialoperatoren 2. Ordnung entsprechen, wenn man die partiellen Ableitungen 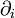$\partial_i$ formal durch Variablen y_i ersetzt und nur die Terme höchster - also zweiter - Ordnung betrachtet, einer quadratischen Form in den y_i. Im elliptischen Fall haben alle Koeffizienten der Form ein Vorzeichen, im hyperbolischen Fall wechselt das Vorzeichen, im parabolischen Fall fehlt für eines der y_i der Term höchster Ordnung. Die partiellen Differentialgleichungen zeigen jeweils sehr unterschiedliches Verhalten. Die Namen kommen von den Analoga zu Kegelschnittgleichungen.

Das lässt sich durch den Begriff des Symbols des Differentialoperators auch auf andere Fälle erweitern. Man behält nur Terme der höchsten Ordnung bei, ersetzt Ableitungen durch neue Variable y_i und erhält ein Polynom in diesen neuen Variablen, mit dem man den Differentialoperator charakterisieren kann. Beispielsweise ist er vom elliptischen Typ, wenn gilt: das Symbol ist ungleich Null, wenn mindestens ein y_i ungleich Null ist. Es gibt aber schon bei Differentialoperatoren 2. Ordnung „gemischte“ Fälle, die keiner der drei Klassen zuzuordnen sind.