Quotientengruppe

Die Faktorgruppe ist eine Gruppe, die mittels einer Standardkonstruktion aus einer gegebenen Gruppe G unter Zuhilfenahme eines Normalteilers 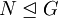$N \trianglelefteq G$ gebildet wird. Sie wird mit G / N bezeichnet.

Konstruktion

Die Elemente von G / N sind hierbei die Nebenklassen bezüglich N, also

$G/N := \{ gN : g \in G \}$.

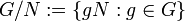Schließlich benötigt man noch eine innere Verknüpfung 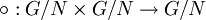$\circ: G/N \times G/N \rightarrow G/N$, nämlich

$(gN) \circ (hN) := (gh)N$.

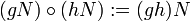Man kann aus der Normalteilereigenschaft von N zeigen, dass 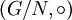$(G/N, \circ)$ eine Gruppe ist, die sogenannte Faktorgruppe, und dass 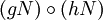$(gN) \circ (hN)$ mit dem Komplexprodukt 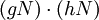$(gN)\cdot(hN)$ übereinstimmt. Die Ordnung der Faktorgruppe G / N wird der Index von N in G genannt und mit (G:N) bezeichnet.

In abelschen Gruppen ist jede Untergruppe Normalteiler. Somit lässt sich dort nach jeder Untergruppe die Faktorgruppe bilden, welche dann wiederum abelsch ist.

Beispiel

Restklassengruppe der additiven Gruppe der ganzen Zahlen

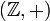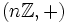Die Gruppe $(\mathbb{Z}, +)$ ist eine abelsche Gruppe. Für jedes $n \in \mathbb{N}$ ist $(n\mathbb{Z}, +)$ eine Untergruppe, also ein Normalteiler von 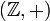$(\mathbb{Z},+)$. Die Faktorgruppe 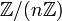$\mathbb{Z}/(n\mathbb{Z})$ wird als Restklassengruppe modulo n bezeichnet.

Ihre Elemente werden als

$[k] := k + (n\mathbb{Z}) = \{k+m\ :\ m \in n\mathbb{Z}\} = \{k+nz\ :\ z \in \mathbb{Z}\}$

geschrieben und heißen Kongruenzklassen bezüglich der Addition modulo n. Es ist also

$\mathbb{Z}/(n\mathbb{Z}) = \{[0], [1], \ldots, [n-1]\}$.

Die innere Verknüpfung von 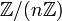$\mathbb{Z}/(n\mathbb{Z})$ wird üblicherweise wieder mit + bezeichnet. In 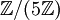$\mathbb{Z} /(5\mathbb{Z})$ gilt beispielsweise

$\ [3] + [4] = [2]$,

da 3 + 4 = 7 = 2 + 5, also $(3+4) + 5\mathbb{Z} = 2 + 5\mathbb{Z}$.

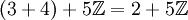Faktorgruppe nach Kernen von Homomorphismen

Im Falle eines Gruppenhomomorphismus 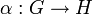$\alpha: G \rightarrow H$ zwischen zwei Gruppen G und H ist der Kern von α ein Normalteiler von G und das Bild von α eine Untergruppe von H. Daher ist 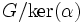$\ G/{\rm ker}(\alpha)$ eine Faktorgruppe. Der Homomorphiesatz für Gruppen besagt, dass diese Faktorgruppe isomorph zum Bild von α ist.

Literatur

• Kurt Meyberg: Algebra, Teil 1. 2. Auflage, Carl Hanser Verlag 1980, ISBN 3-446-13079-9

Siehe auch

Gruppentheorie-Glossar, Gruppe