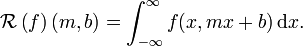- Radontransformation
-
Die Radon-Transformation (benannt nach dem österreichischen Mathematiker Johann Radon, der sie 1917 in einer Veröffentlichung Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten einführte) ist die folgende Integraltransformation:
Hierbei ist f eine Funktion in der Ebene, wobei vorausgesetzt wird, dass die Funktion stetig und außerhalb eines Kreises von endlichem Radius identisch Null ist.
Das Problem ist ein schlecht gestelltes Problem[1]. In diesem Fall hängt die Lösung des Problems nicht stetig von den Eingangsdaten ab. Um das Problem dennoch hinreichend genau zu lösen, können Regularisierungstechniken angewandt werden.
Anwendung der Radon-Transformation
Die Umkehrung der Radon-Transformation wird in der Tomographie, etwa in der Computertomographie verwendet, um aus den gemessenen Projektionen das zweidimensionale Bild zurückzugewinnen.
Bei der Computer-Tomographie wird ein dreidimensionales Objekt mit Strahlen aus unterschiedlichen Richtungen durchstrahlt. Das am Detektor ankommende Signal ist jeweils die Radon-Transformierte des durchleuchteten Objektes. Diese lässt sich mit mathematischen Methoden (insbesondere aus der Fourieranalyse) umkehren, so dass ein Bild des Objektes errechnet wird. Das Objekt wird dabei schichtenweise untersucht. Am Ende lässt sich aus den Bildern der Schichten ein dreidimensionales Bild des Objektes erzeugen.
Einzelnachweise
- ↑ A.K. Louis, Inverse und schlecht gestellte Probleme, Teubner, 1989 (Kap. 6.1. und 6.2)
Weblinks
Wikimedia Foundation.