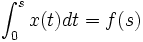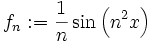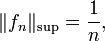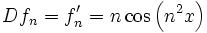- Integralgleichungen 1. Art
-
In der Mathematik wird eine Integralgleichung, bei der die gesuchte Funktion nur unter dem Integralzeichen vorkommt, als Integralgleichung 1. Art bezeichnet. Sind beispielsweise
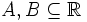 ,
, 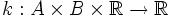 und
und 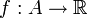 gegeben, so ist
gegeben, so isteine Integralgleichung der 1. Art für die unbekannte Funktion
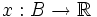 .
.Inhaltsverzeichnis
Einteilung
Sind die Grenzen des Integrals fix, so wird die Integralgleichung Fredholmsch genannt; tritt die freie Variable in den Integralgrenzen auf, so heißt die Integralgleichung Volterrasch.
Ein einfaches Beispiel einer Volterraschen Integralgleichung 1. Art ist die Gleichung
deren Lösung offensichtlich die erste Ableitung ist:
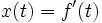 .
.Lösbarkeit
Integralgleichungen 1. Art sind in der Regel sogenannte inkorrekt gestellte Probleme, also Probleme, die nicht in kanonischer Weise gelöst werden können. Ist nämlich
ein kompakter Operator zwischen Banachräumen X und Y und hat K unendlich-dimensionalen Bildraum, dann ist das Bild von K von erster Kategorie in Y. Das bedeutet, dass K nicht stetig invertierbar oder wenigstens offen sein kann. Zur Lösung von Integralgleichungen 1. Art sind daher Regularisierungsverfahren erforderlich.
Beispiel
Auch das bereits erwähnte Bilden der ersten Ableitung ist ein inkorrekt gestelltes Problem: Betrachtet man beispielsweise den normierten Vektorraum
der unendlich oft stetig differenzierbaren Funktionen des Intervalls
![[0,1]\;](/pictures/dewiki/48/0ccfe73327271e91a28e86855315af81.png) bezüglich der Supremumsnorm, so ist der Operator
bezüglich der Supremumsnorm, so ist der Operatorwelcher der Funktion
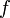 die Lösung der Integralgleichung
die Lösung der Integralgleichungzuordnet, ein unstetiger linearer Operator:
ist im Sinne der Supremumsnorm eine Nullfolge, da
aber für
gilt:
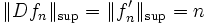 .
.
Die Funktionenfolge
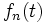 konvergiert also gegen die Funktion
konvergiert also gegen die Funktion 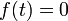 , aber die Folge
, aber die Folge 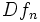 der Bilder divergiert.
der Bilder divergiert.Numerisches Differenzieren
Diese Eigenschaft spiegelt sich auch wider, wenn man versucht, näherungsweise gegebene Funktionen numerisch zu differenzieren. Berechnet man beispielsweise numerisch die Ableitung von ex an der Stelle x = 0,5 durch Bilden der Differenzenquotienten
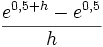 für unterschiedliche Schrittweiten h, so erhält man typischerweise folgendes Ergebnis:
für unterschiedliche Schrittweiten h, so erhält man typischerweise folgendes Ergebnis: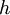
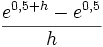
1 2,83297 0,1 1,73398 0,01 1.65699 0,001 1,64955 0,0001 1,6488 10 − 5 1,64873 10 − 6 1,64872 10 − 7 1,64872 10 − 8 1,64872 10 − 9 1,64872 10 − 10 1,64872 10 − 11 1,64873 10 − 12 1,64868 10 − 13 1,64979 10 − 14 1,64313 10 − 15 1,55431 10 − 16 2,22045 Der exakte Wert der Ableitung ist
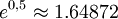 . Der Fehler nimmt für immer kleinere Schrittweiten h also zuerst ab bis man praktisch den korrekten Wert erhält, für noch kleinere h nimmt der Fehler aber überraschenderweise wieder zu. Dies erklärt sich damit, dass für kleine h zwar der Diskretisierungsfehler, also der Unterschied zwischen dem Differenzenquotienten und der Ableitung, immer kleiner wird, dafür aber nimmt der Fehler zu, der dadurch entsteht, dass man ja ex nicht exakt zur Verfügung hat, sondern nur eine numerische Approximation dieser Funktion. Da Differenzieren ein unstetiger linearer Operator ist, kann dieser zweite Fehler beliebig groß werden.
. Der Fehler nimmt für immer kleinere Schrittweiten h also zuerst ab bis man praktisch den korrekten Wert erhält, für noch kleinere h nimmt der Fehler aber überraschenderweise wieder zu. Dies erklärt sich damit, dass für kleine h zwar der Diskretisierungsfehler, also der Unterschied zwischen dem Differenzenquotienten und der Ableitung, immer kleiner wird, dafür aber nimmt der Fehler zu, der dadurch entsteht, dass man ja ex nicht exakt zur Verfügung hat, sondern nur eine numerische Approximation dieser Funktion. Da Differenzieren ein unstetiger linearer Operator ist, kann dieser zweite Fehler beliebig groß werden.Dieses Verhalten ist generell typisch für inkorrekt gestellte Probleme.
Weitere Beispiele
Andere Beispiele von Integralgleichungen 1. Art sind die inverse Laplacetransformation sowie die nach Johann Radon benannte inverse Radontransformation, die in der Computertomografie eine wichtige Rolle spielt. Beides sind inkorrekt gestellte Probleme.
Die inverse Fouriertransformation ist ebenfalls eine Integralgleichung 1. Art, im Gegensatz zu den anderen Beispielen allerdings ein korrekt gestelltes Problem.
Wikimedia Foundation.

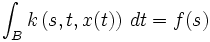
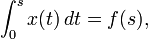
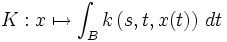
![\left(C^\infty\left([0,1]\right),\|.\|_{\sup} \right)](/pictures/dewiki/98/b2cd39041ff182489f6c95a81c210848.png)
![D:\begin{cases} C^\infty\left([0,1]\right) \to C^\infty\left([0,1]\right)\\ f\mapsto f'\end{cases},](/pictures/dewiki/54/6d8e1e4f52a8546d1300d36bf28939c7.png)