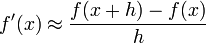Auslöschung (Numerik)

Unter Auslöschung (engl. cancellation) versteht man in der Numerik den Verlust an Genauigkeit bei der Subtraktion fast gleichgroßer Gleitkommazahlen.

Beispiele

Zahlenbeispiel

Will man die Zahlen a=2,345678 und b=2,346789 voneinander subtrahieren so erwartet man als Ergebnis

b-a=0,001111

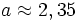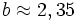Rechnet man allerdings mit 2 Nachkommastellen Genauigkeit so erhält man: $a\approx2,35$ und $b\approx2,35$ und somit als Ergebnis

b-a=0

Wünschenswert wäre es, bei dieser Rechnung 3 gültige Stellen (z.B. 1.11e-3 oder 0.00111) zu erhalten. Das berechnete Ergebnis enthält aber keine gültigen Stellen mehr. Dieser Effekt wird als Auslöschung bezeichnet.

Beispiel: Algorithmus des Archimedes zur Kreiszahlberechnung

Berechnung von pi nach Archimedes

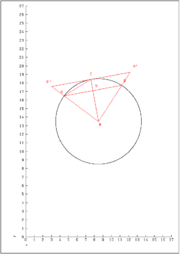
Archimedes von Syrakus bewies, dass sich der Umfang eines Kreises zu seinem Durchmesser genauso verhält, wie die Fläche des Kreises zum Quadrat des Radius. Er nannte dieses (heute als Kreiszahl bezeichnete) Verhältnis noch nicht π, gab aber eine Anleitung, wie man sich mit Hilfe von ein- und umschriebenen Vielecken dem Verhältnis bis zu einer beliebig hohen Genauigkeit nähern kann, vermutlich eines der ältesten numerischen Verfahren der Geschichte. Und er führte die Berechnung bis zum 96-Eck mit dem folgenden Resultat durch:

$3{,}1408450 \dots = 3 + \frac{10}{71} <\pi< 3 + \frac{10}{70} = 3{,}1428571 \dots$

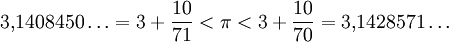
Wie man dem Zahlenbeispiel entnehmen kann, hatte Archimedes keine Chance, beim 96-Eck die Auslöschung überhaupt nur wahrzunehmen.

In heutiger Sprache beginnt man mit direkt berechenbaren Seitenlängen s_n = AB von in einem Einheitskreis (MA = MB = MC = 1) einbeschriebenen Vielecken, z. B. dem Zweieck s₂ = 2, dem Dreieck 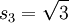$s_3 = \sqrt{3}$, dem Viereck 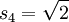$s_4 = \sqrt{2}$ oder dem Sechseck s₆ = 1.

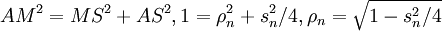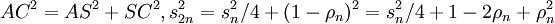Dann ist für Vielecke mit doppelter Eckenzahl deren Seitenlänge s_2n = AC mit der Hilfsstrecke ρ_n = MS und zweimaliger Anwendung des Satzes von Pythagoras ($AM^2 = MS^2 + AS^2, 1 = \rho_n^2 + s_n^2/4, \rho_n = \sqrt{1-s_n^2/4}$ und $AC^2 = AS^2 + SC^2, s_{2n}^2 = s_n^2/4 + (1-\rho_n)^2 = s_n^2/4 + 1 - 2 \rho_n + \rho_n^2$) leicht herleitbar: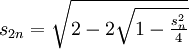

$s_{2n}=\sqrt{2-2\sqrt{1-\tfrac{s_n^2}{4}}}$

Mit den vier Grundrechenarten und der Quadratwurzel kann man also beginnend mit dem Zweieck die Seitenlänge und den Umfang eines einbeschriebenen Vielecks und damit indirekt eine Näherung für π berechnen. In der Praxis ist das Ergebnis jedoch enttäuschend. Die folgende Tabelle zeigt beginnend mit n=2 den Abstand 1 − ρ_n der Seitenmitte S zum Kreisrand, die Seitenlängen s_n des eingeschriebenen und 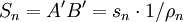$S_n = A'B' = s_n \cdot 1 / \rho_n$ des umschriebenen n-Ecks und deren Flächen a_n = ns_nρ_n / 2 und A_n = nS_n / 2, die beim Einheitskreis gegen π konvergieren sollten. Die Rechnung wurde in C mit double nach IEEE 754 und somit ca 15 Dezimalstellen durchgeführt. Die Zahlenwerte sind aber auch mit jedem Taschenrechner, der Quadratwurzeln beherrscht, nachvollziehbar:

n             1 − ρn        sn         Sn            an                 An
2          1.000e+00  2.00e+00       Inf  0.00000000000000               Inf
4          2.929e-01  1.41e+00  2.00e+00  2.00000000000000  4.00000000000000
8          7.612e-02  7.65e-01  8.28e-01  2.82842712474619  3.31370849898476
16         1.921e-02  3.90e-01  3.98e-01  3.06146745892072  3.18259787807453
32         4.815e-03  1.96e-01  1.97e-01  3.12144515225805  3.15172490742926
64         1.205e-03  9.81e-02  9.83e-02  3.13654849054593  3.14411838524589
128        3.012e-04  4.91e-02  4.91e-02  3.14033115695474  3.14222362994244
256        7.530e-05  2.45e-02  2.45e-02  3.14127725093262  3.14175036916881
512        1.882e-05  1.23e-02  1.23e-02  3.14151380114509  3.14163208070397
1024       4.706e-06  6.14e-03  6.14e-03  3.14157294036989  3.14160251025961
2048       1.177e-06  3.07e-03  3.07e-03  3.14158772527060  3.14159511774302
4096       2.941e-07  1.53e-03  1.53e-03  3.14159142155216  3.14159326967027
8192       7.353e-08  7.67e-04  7.67e-04  3.14159234553025  3.14159280755978
1.638e+04  1.838e-08  3.83e-04  3.83e-04  3.14159257570956  3.14159269121694
3.277e+04  4.596e-09  1.92e-04  1.92e-04  3.14159264036917  3.14159266924601
6.554e+04  1.149e-09  9.59e-05  9.59e-05  3.14159264171161  3.14159264893082
1.311e+05  2.872e-10  4.79e-05  4.79e-05  3.14159260647332  3.14159260827812
2.621e+05  7.181e-11  2.40e-05  2.40e-05  3.14159291071407  3.14159291116527
5.243e+05  1.795e-11  1.20e-05  1.20e-05  3.14159169662728  3.14159169674009
1.049e+06  4.488e-12  5.99e-06  5.99e-06  3.14159655369072  3.14159655371892
2.097e+06  1.122e-12  3.00e-06  3.00e-06  3.14159655370129  3.14159655370834
4.194e+06  2.804e-13  1.50e-06  1.50e-06  3.14151884046467  3.14151884046643
8.389e+06  7.017e-14  7.49e-07  7.49e-07  3.14120796828205  3.14120796828249
1.678e+07  1.754e-14  3.75e-07  3.75e-07  3.14245127249408  3.14245127249419
3.355e+07  4.441e-15  1.87e-07  1.87e-07  3.14245127249412  3.14245127249415
6.711e+07  1.110e-15  9.42e-08  9.42e-08  3.16227766016838  3.16227766016838
1.342e+08  2.220e-16  4.71e-08  4.71e-08  3.16227766016838  3.16227766016838
2.684e+08  0.000e+00  2.11e-08  2.11e-08  2.82842712474619  2.82842712474619
5.369e+08  0.000e+00  0.00e+00  0.00e+00  0.00000000000000  0.00000000000000

Man erkennt deutlich am Anfang die Konvergenz gegen pi. Nach Erreichen etwa der halben Stellenzahl beim 32768-Eck macht sich jedoch die Auslöschung bei der Subtraktion der fast gleichgroßen Zahlen 2 und 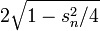$2\sqrt{1-s_n^2/4}$ bemerkbar. Das Ergebnis wird jetzt wieder ungenauer und am Ende falsch (2-2.000...000xxx = 0).

In vielen Fällen, so auch hier, kann man die Auslöschung vermeiden, einfach indem man die betroffenen Subtraktionen vermeidet. Hier gelingt das mit einer Umformung der Formel in eine äquivalente Form ohne Subtraktion unter Anwendung von

$a^2 - b^2 = (a+b)(a-b); a-b = \frac{a^2-b^2}{a+b}$

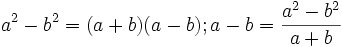
mit $a=2, b=2\sqrt{1-\tfrac{s_n^2}{4}}$

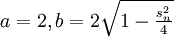
Es ergibt sich:

$s_{2n}=\sqrt{2-2\sqrt{1-\frac{s_n^2}{4}}}=\sqrt{\frac{4-4(1-\frac{s_n^2}{4})}{2+2\sqrt{1-\frac{s_n^2}{4}}}}=\sqrt{2\frac{1-1+\frac{s_n^2}{4}}{1+\sqrt{1-\frac{s_n^2}{4}}}}=\sqrt{\frac{1}{2}s_n^2\frac{1}{1+\sqrt{1-\frac{s_n^2}{4}}}}$

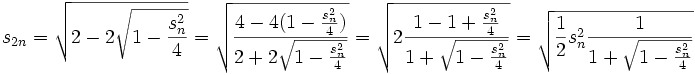
Natürlich ist es ein glücklicher Zufall, dass sich im Zähler die Subtraktion „weghebt“. Jetzt verläuft die Rechnung wie erwünscht:

n             1 − ρn        sn         Sn            an                 An
2.000e+00  1.000e+00  2.00e+00       Inf  0.00000000000000               Inf
4.000e+00  2.929e-01  1.41e+00  2.00e+00  2.00000000000000  4.00000000000000
8.000e+00  7.612e-02  7.65e-01  8.28e-01  2.82842712474619  3.31370849898476
1.600e+01  1.921e-02  3.90e-01  3.98e-01  3.06146745892072  3.18259787807453
3.200e+01  4.815e-03  1.96e-01  1.97e-01  3.12144515225805  3.15172490742926
6.400e+01  1.205e-03  9.81e-02  9.83e-02  3.13654849054594  3.14411838524590
1.280e+02  3.012e-04  4.91e-02  4.91e-02  3.14033115695475  3.14222362994246
2.560e+02  7.530e-05  2.45e-02  2.45e-02  3.14127725093277  3.14175036916897
5.120e+02  1.882e-05  1.23e-02  1.23e-02  3.14151380114430  3.14163208070318
1.024e+03  4.706e-06  6.14e-03  6.14e-03  3.14157294036709  3.14160251025681
2.048e+03  1.177e-06  3.07e-03  3.07e-03  3.14158772527716  3.14159511774959
4.096e+03  2.941e-07  1.53e-03  1.53e-03  3.14159142151120  3.14159326962931
8.192e+03  7.353e-08  7.67e-04  7.67e-04  3.14159234557012  3.14159280759964
1.638e+04  1.838e-08  3.83e-04  3.83e-04  3.14159257658487  3.14159269209225
3.277e+04  4.596e-09  1.92e-04  1.92e-04  3.14159263433856  3.14159266321541
6.554e+04  1.149e-09  9.59e-05  9.59e-05  3.14159264877699  3.14159265599620
1.311e+05  2.872e-10  4.79e-05  4.79e-05  3.14159265238659  3.14159265419140
2.621e+05  7.181e-11  2.40e-05  2.40e-05  3.14159265328899  3.14159265374019
5.243e+05  1.795e-11  1.20e-05  1.20e-05  3.14159265351459  3.14159265362739
1.049e+06  4.488e-12  5.99e-06  5.99e-06  3.14159265357099  3.14159265359919
2.097e+06  1.122e-12  3.00e-06  3.00e-06  3.14159265358509  3.14159265359214
4.194e+06  2.804e-13  1.50e-06  1.50e-06  3.14159265358862  3.14159265359038
8.389e+06  7.017e-14  7.49e-07  7.49e-07  3.14159265358950  3.14159265358994
1.678e+07  1.754e-14  3.75e-07  3.75e-07  3.14159265358972  3.14159265358983
3.355e+07  4.441e-15  1.87e-07  1.87e-07  3.14159265358978  3.14159265358980
6.711e+07  1.110e-15  9.36e-08  9.36e-08  3.14159265358979  3.14159265358980
1.342e+08  2.220e-16  4.68e-08  4.68e-08  3.14159265358979  3.14159265358979
2.684e+08  0.000e+00  2.34e-08  2.34e-08  3.14159265358979  3.14159265358979

Schon bei dem 268435456-Eck erreicht man die volle Genauigkeit von knapp 16 Dezimalstellen. Das Abbruchsignal gibt die 0 in der zweiten Spalte.

Faustregel

Subtrahiert man zwei fast gleichgroße Zahlen, die in den ersten k Stellen übereinstimmen, so gehen im Ergebnis von den eigentlich möglichen p Stellen k verloren. Es sind also nur noch p − k Stellen vertrauenswürdig.

Differentialrechnung

Bei der numerischen Berechnung von Ableitungen durch Differenzenquotienten wie zum Beispiel

$f'(x) \approx \frac{f(x+h)-f(x)}{h}$

tritt bei zu kleinem h Auslöschung auf, da die Funktionswerte dann nahezu gleich sind.