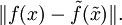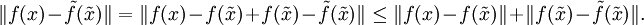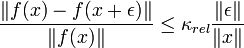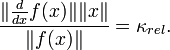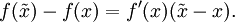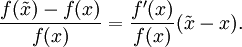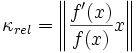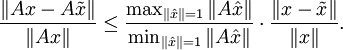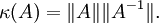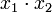- Konditionszahl
-
In der numerischen Mathematik beschreibt man mit der Kondition die Abhängigkeit der Lösung eines Problems von der Störung der Eingangsdaten. Die Konditionszahl stellt ein Maß für diese Abhängigkeit dar; sie beschreibt den Faktor, um den der Eingangsfehler im ungünstigsten Fall verstärkt wird. Sie ist unabhängig von konkreten Lösungsverfahren.
Inhaltsverzeichnis
Einleitung
In der Numerik unterscheidet man zwischen den drei Größen eines Verfahrens: Kondition, Stabilität und Konsistenz, die untereinander stark verwandt sind. Die Beziehung zwischen Kondition eines Problems und Stabilität lässt sich wie folgt modellieren:
Es sei
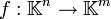 das mathematische Problem in Abhängigkeit von der Eingabe x, und es sei
das mathematische Problem in Abhängigkeit von der Eingabe x, und es sei 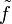 der numerische Algorithmus sowie
der numerische Algorithmus sowie 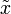 die gestörten Eingabedaten. So möchte man den folgenden Fehler abschätzen:
die gestörten Eingabedaten. So möchte man den folgenden Fehler abschätzen:Mit der Dreiecksungleichung gilt:
Hierbei bezeichnet man mit
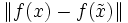 die Kondition des Problems und mit
die Kondition des Problems und mit 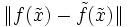 die Stabilität. Man spricht dann davon, dass Kondition die Eigenschaft des Problems und Stabilität die Eigenschaft des Algorithmus ist.
die Stabilität. Man spricht dann davon, dass Kondition die Eigenschaft des Problems und Stabilität die Eigenschaft des Algorithmus ist.Absolute Kondition
Die absolute Kondition κabs ist definiert als
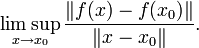
Also ist die absolute Kondition κabs genau die kleinste Zahl, für die gilt:
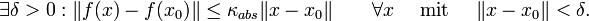
Relative Kondition
Die relative Kondition wird definiert als kleinste Zahl
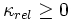 mit der Eigenschaft: Es gibt ein δ > 0, so dass für alle 0 < ε < δ die Ungleichung
mit der Eigenschaft: Es gibt ein δ > 0, so dass für alle 0 < ε < δ die Ungleichunggilt.
Dabei ist
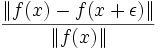 die relative Änderung des Funktionswertes und
die relative Änderung des Funktionswertes und 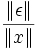 die relative Änderung des Parameters.
die relative Änderung des Parameters.Aus der Definition folgt durch Umstellen, dass für eine in x differenzierbare Funktion κrel gegeben ist durch
Herleitung der relativen Konditionszahl aus der Taylor-Reihe
Lässt man in der Taylorreihe Terme höherer Ordnung unberücksichtigt, so ergibt sich
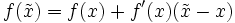 ,
,
folglich
Hierbei stellt
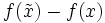 den absoluten Fehler in der Ausgabe dar. Durch Division durch f(x) ergibt sich sofort der relative Ausgabefehler:
den absoluten Fehler in der Ausgabe dar. Durch Division durch f(x) ergibt sich sofort der relative Ausgabefehler:Um den relativen Fehler in der Eingabe auf der rechten Seite sichtbar zu machen, wird nun noch mit x erweitert:
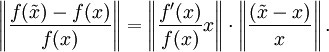
Somit ist alleine aus der Taylorreihe ersichtlich, dass die Fehlerverstärkung durch
in guter Näherung (Terme höherer Ordnung wurden vernachlässigt!) beschrieben ist.
Kondition von Linearen Abbildungen
Die Kondition von linearen Abbildungen lässt sich mithilfe der relativen Kondition herleiten. Setzt man für f(x) in obiger Definition die Funktion f(x) = Ax ein, so gilt:
Damit ist die Kondition von Matrizen die größtmögliche Verzerrung der Einheitskugel:
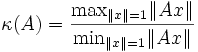 .
.
Ist der Kern der Matrix nicht trivial, d. h. gibt es von Null verschiedene Vektoren, die auf die Null abgebildet werden, dann ist
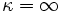 . Umgekehrt kann man zeigen, dass für reguläre Matrizen gilt:
. Umgekehrt kann man zeigen, dass für reguläre Matrizen gilt:Interpretation
Ist die Konditionszahl κ deutlich größer als 1, spricht man von einem schlecht konditionierten Problem, sonst von einem gut konditionierten Problem und ist die Konditionszahl unendlich, so handelt es sich um ein schlecht gestelltes Problem.
Die Bedeutung der Kondition wird deutlich, wenn man sich den Unterschied zwischen den realen Eingangsdaten (beispielsweise reelle Zahlen) und den tatsächlichen Eingangsdaten in Form von Maschinenzahlen klar macht. Es liegen also einem Computerprogramm stets bereits verfälschte Daten vor. Das Computerprogramm sollte nun ein brauchbares Ergebnis liefern. Wenn aber das Problem bereits schlecht konditioniert ist, darf man nicht erwarten, dass der Algorithmus brauchbare Ergebnisse liefert.
Beispiele
Multiplikation
Die Multiplikation ist eine Abbildung
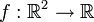 gegeben durch
gegeben durch 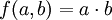 . Die partiellen Ableitungen nach a,b führen zu
. Die partiellen Ableitungen nach a,b führen zu 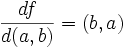 . Damit ergibt sich für die Kondition der Multiplikation nach obiger Formel
. Damit ergibt sich für die Kondition der Multiplikation nach obiger Formel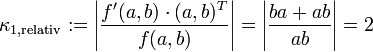 .
.Die Multiplikation kann als gut konditioniert angesehen werden.
Addition
Addition: x1 + x2
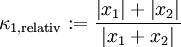
Die Addition ist daher für
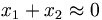 , die Subtraktion entsprechend im Fall
, die Subtraktion entsprechend im Fall 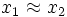 , sehr schlecht konditioniert. In diesem Fall spricht man von Auslöschung.
, sehr schlecht konditioniert. In diesem Fall spricht man von Auslöschung.Numerische Aspekte
Eines der Aufgabengebiete der Numerik ist die Untersuchung und Optimierung der Kondition für gegebene Probleme wie das Lösen von Gleichungssystemen. Bei der numerischen Lösung wird nun ein Problem in Teilprobleme zerlegt. Oft kann ein in schlecht konditionierte Probleme zerlegter Lösungsweg so durch eine geschicktere Zerlegung ersetzt werden, dass sich die Gesamt-Kondition entscheidend verbessert. So erreicht man bei Matrizen durch geschickte Zeilenvertauschung eine bessere Gesamt-Kondition (hierbei wird die Kondition der Matrix an sich nicht verändert); bei längeren Berechnungen versucht man Additionen sehr kleiner Zahlen oder Subtraktionen annähernd gleich großer Zahlen zur Vermeidung von Auslöschung zu umgehen.
Die äquivalente Umformulierung eines Problems mit dem Ziel der Konditionsverbesserung nennt man Vorkonditionierung.
Zum Testen numerischer Verfahren an Matrizen mit besonders schlechter Kondition eignen sich die Hilbert-Matrizen.
Literatur
- Deuflhard, Hohmann: Numerische Mathematik I. 3. Auflage. Gruyter, 2002, ISBN 978-3110171822.
Wikimedia Foundation.