Archimedes

Archimedes, Domenico Fetti, 1620, Gemäldegalerie Alte Meister, Dresden

Archimedes (griechisch ᾿Αρχιμήδης) von Syrakus (* um 287 v. Chr. vermutlich in Syrakus auf Sizilien; † 212 v. Chr. ebenda) war ein antiker griechischer Mathematiker, Physiker und Ingenieur. Er gilt als einer der bedeutendsten Mathematiker der Antike. Seine Werke waren auch noch im 16. und 17. Jahrhundert bei der Entwicklung der höheren Analysis von Bedeutung.

Leben

Archimedes war der Sohn des Hetophoras, eines Astronomen am Hof des Hieron von Syrakus. Bei einem längeren Aufenthalt in Alexandria lernte Archimedes die dortigen Mathematiker Konon, Dositheos und Eratosthenes kennen, mit denen er später weiter korrespondierte. In Syrakus war er mit König Hieron II. und dessen Sohn und Mitregent Gelon II. befreundet.

Archimedes war an der Verteidigung von Syrakus gegen die römische Belagerung im Zweiten Punischen Krieg beteiligt. Bei der Eroberung von Syrakus – nach dreijähriger Belagerung durch den römischen Feldherrn M. Claudius Marcellus – wurde Archimedes von einem römischen Soldaten getötet.

Die erhaltenen Traktate

• De planorum equilibris
• De quadratura parabolae (Quadratur der Parabel), Inhalt: Fläche eines Parabelsegments.
• De sphaera et cylindro (Kugel und Zylinder), Inhalt: Volumen von Kugel und Zylinder.
• De spiralibus (Über Spiralförmige Linien), Inhalt: Fläche eines von ihm erfundenen Objekts, der Spirallinie.
• De conoidibus et sphaeroidibus (Über Konoide und Sphäroide), Inhalt: Volumina von Hyberbeln und Ellipsen.
• De corporibus natantibus (Über schwimmende Körper), Inhalt: Volumen und spezifisches Gewicht von Körpern.
• Dimensio circuli
• Arenarius (Griech. Psammites, deutsch: die Sandrechnung), Inhalt: Darstellung beliebig großer Zahlen, Heliozentrisches Weltbild des Aristarchos von Samos
• Problema boum
• De methodo (Fragment)
• Ostomachion (Fragment, Zuschreibung fraglich)
• Liber assumptorum (wohl nicht archimedisch)

siehe auch: Das Palimpsest des Archimedes

Werk

Mittelalterliches Idealporträt von Archimedes

Archimedes war sowohl in der Mathematik als auch im Bereich der heutigen Physik gleichermaßen schöpferisch tätig. Ihm zu Ehren wurde auf dem Mare Imbrium ein Mondkrater Archimedes genannt; siehe Archimedes (Mondkrater).

Physik

Hebelgesetz

Archimedes formulierte die Hebelgesetze und schuf dadurch die theoretische Grundlage für die spätere Entwicklung der Mechanik. Er selbst entwickelte aus dem Hebelgesetz bereits die wissenschaftlichen Grundlagen der Statik für statisch bestimmte Systeme.

Er soll angeblich gesagt haben: „Gib mir einen Punkt, auf dem ich stehen kann, und ich werde dir die Welt aus den Angeln heben“. Darauf gründet sich der Begriff des archimedischen Punktes.

Archimedisches Prinzip

Archimedes sollte den Gold-Gehalt der Krone des Herrschers Hieron II. prüfen, ohne sie jedoch zu beschädigen. Um die gestellte Aufgabe zu lösen, tauchte er einmal die Krone und dann einen Goldbarren, der genauso viel wog wie die Krone, in einen vollen Wasserbehälter und maß die Menge des überlaufenden Wassers. Die Krone verdrängte mehr Wasser als der Goldbarren. Dadurch war bewiesen, dass die Krone ein kleineres spezifisches Gewicht hatte und daher nicht ganz aus Gold gefertigt war. Archimedes soll das Auftriebsprinzip durch einen Geistesblitz beim Baden entdeckt haben, als aus dem randvollen Wasserbehälter plötzlich jene Wassermenge auslief, die er beim Hineinsteigen ins Bad mit seinem Körpervolumen verdrängte. Vor Freude glücklich über seine Entdeckung, lief er mit dem Ausruf „Heureka!“ (altgriechisch: εὕρηκα /hɛːǔ̯rɛːka/, „Ich hab’s gefunden!“) nackt auf die Straße.

Das Auftriebsprinzip wird nach seinem Entdecker archimedisches Prinzip genannt. Es kann bei jedem schwimmenden Körper Anwendung finden und stellt beim Schiffbau eine zwingend zu berücksichtigende Tatsache dar. Damit begründete Archimedes das hydrostatische Grundgesetz, dessen Wissen jedoch wieder verloren ging und erst um 1750 von Leonhard Euler und Bouguer wiederentdeckt und angewendet wurde. Archimedes war auch die unterschiedliche Dichte von Flüssigkeiten bekannt, so unterschied er z. B. zwischen Meeresschiffen und solchen, die im Süßwasser eingesetzt werden sollten.

Bei seinen hydrostatischen Experimenten entdeckte er das Prinzip der kommunizierenden Gefäße.

Mathematik

Bronzeskulptur von Archimedes im Treptower Park bei der Archenhold-Sternwarte in Berlin (Gerhard Thieme 1972)

Flächenberechnungen

Archimedes bewies, dass sich der Umfang eines Kreises zu seinem Durchmesser genauso verhält, wie die Fläche des Kreises zum Quadrat des Radius. Er nannte dieses (heute als Pi oder Kreiszahl bezeichnete) Verhältnis noch nicht π (Pi), gab aber eine Anleitung, wie man sich dem Verhältnis bis zu einer beliebig hohen Genauigkeit nähern kann, vermutlich das älteste numerische Verfahren der Geschichte. Mit seinen Überlegungen zur Flächen- und Volumenberechnung (u. a. mit einer exakten Quadratur der Parabel) nahm Archimedes Ideen der Integralrechnung viel später folgender Denker vorweg. Er ging dabei über die Eudoxos von Knidos zugeschriebene Exhaustionsmethode (Ausschöpfungsmethode) hinaus, beispielsweise wandte er bereits eine Form des Prinzips von Cavalieri an.

Archimedes benutzte auch eine damals neue Methode, um Hypothesen zum Flächeninhalt krummlinig begrenzter Flächen (z. B. von Parabeln und Quadraten) praktisch zu überprüfen. Er zeichnete die entsprechenden Flächen auf dünne Tafeln (z. B. aus Holz, mehrlagigem Papyrus oder vielleicht auch Ton) auf und schnitt sie anschließend aus. Danach verglich er das Gewicht der ausgeschnittenen Flächenstücke. Dadurch konnte er falsche Hypothesen durch Messung des Gewichts bereits von vorneherein ausschließen.

1906 fand Johan Ludvig Heiberg (1854–1928), ein dänischer Philologe und Professor an der Universität Kopenhagen in Istanbul ein auf das 10. Jahrhundert datiertes Manuskript, das unter anderem eine Abschrift von Archimedes’ Schrift Die Methode enthielt.^[1][2]

Stellenwertbasiertes Zahlensystem

Außerdem entwickelte Archimedes ein stellenwertbasiertes Zahlensystem mit der Basis 10⁸.

Er benutzte es, um astronomisch große Zahlen (bis zur Größe von 10⁶⁴) mathematisch fassen zu können – dies in einer Zeit, in der seine Mitwelt eine Myriade (lit. 10.000) bereits mit „unendlich“ gleichsetzte. Anlass dafür war die Abhandlung Über schwimmende Körper und die Sandzahl, auch kurz Sandrechner genannt, die er König Geleon widmete. Darin heißt es: „Es gibt Leute, König Geleon, die der Meinung sind, die Zahl des Sandes sei unendlich groß […] Andere glauben zwar nicht, dass die Zahl unendlich sei, aber doch, dass noch keine Zahl genannt worden sei, die seine Menge übertreffen könnte.“ ^[3]

Er widerlegte diese Vorstellungen, indem er in der Abhandlung die Anzahl der Sandkörner, die alle Strände der Erde bedeckten, abschätzte und benannte. Er ging sogar noch weiter und berechnete die Anzahl der Sandkörner, die man benötigte, um das ganze Universum mit Sand anzufüllen. Damals stellte man sich das Universum allerdings noch wesentlich kleiner vor – nämlich als Kugel von etwa der Größe unseres Sonnensystems. Archimedes’ Rechnung besagt demnach, dass in eine gedachte Kugel von der Größe unseres Sonnensystems etwa 10⁶⁴ Sandkörner hineinpassen würden.

Archimedisches Axiom

Archimedische Schraube

Obwohl nach ihm benannt, stammt das archimedische Axiom nicht von Archimedes, sondern geht auf Eudoxos von Knidos zurück, der dieses Prinzip im Rahmen seiner Größenlehre einführte.

Technik

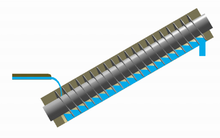
Archimedes hat die Technik seiner Zeit und die spätere Entwicklung der Technik, insbesondere der Mechanik maßgeblich beeinflusst. Er selbst konstruierte allerlei mechanische Geräte – nicht zuletzt auch Kriegsmaschinen – und benutzte Hohlspiegel^[Quelle?] zur Bündelung von Licht. Außerdem wird ihm die Erfindung der sogenannten archimedischen Schraube zugeschrieben.

Legende

Kupferstich auf dem Titelblatt der lateinischen Ausgabe des Thesaurus opticus, einem Werk des arabischen Gelehrten Alhazen. Die Darstellung zeigt, wie Archimedes römische Schiffe mit Hilfe von Parabolspiegeln in Brand gesetzt haben soll.

Archimedes wird nachgesagt, die Römer bei ihrer langwierigen Belagerung mit den von ihm entwickelten Kriegsmaschinen aufgehalten zu haben: So entwickelte er beispielsweise Wurfmaschinen und Katapulte oder auch Seilwinden, welche ein komplettes Schiff, voll beladen und mit gesamter Besatzung, durch Ziehen an einem einzigen Seil bewegten. Auch mächtige Greifarme, die feindliche Boote packten und angeblich in Stücke rissen, gehörten dazu.

Außerdem soll Archimedes die Schiffe der Römer sogar über große Entfernung in Brand gesteckt haben. Mit Hilfe von Spiegeln soll er das Sonnenlicht umgelenkt und auf die angreifenden Schiffe konzentriert haben, so dass ganze Flotten vernichtet wurden. Dazu gibt es eine über 300 Jahre währende, heftige Kontroverse. Historisch sprechen die Quellenlage, Übersetzungsfragen (pyreia wurde oft mit Brennspiegel übersetzt, obwohl es nur „Entzündung“ heißt und auch Brandpfeile umfasst) und das erst Jahrhunderte spätere Auftauchen der Legende dagegen. Physikalische Gegenargumente sind die notwendige Mindestgröße und Brennweite eines solchen Spiegels, die zu erreichende Mindesttemperatur zur Entzündung von Holz und die Zeit, die das zu entzündende Holzstück konstant beleuchtet bleiben muss. Technische Gegenargumente diskutieren die Herstellbarkeit solcher Spiegel zur damaligen Zeit, die Montage eines Spiegels oder Spiegelsystems und die Bedienbarkeit. Ein moderner Kritiker der Legende war der Pyrotechniker Dennis L. Simms^[4]. Forscher des Massachusetts Institute of Technology und der University of Arizona haben 2005 erfolgreich mit 127 kleinen Spiegeln ein 30 Meter entferntes Modell einer Schiffswand entzündet, nachdem der Versuch zuvor mit zwei Spiegeln misslungen war.^[5]

Archimedes’ Legende nach soll er nach der Eroberung von Syrakus dem römischen Soldaten, der ihn festnehmen sollte und ihn gerade beim Zeichnen geometrischer Figuren im Sand störte, zugerufen haben: Noli turbare circulos meos (lateinisch für: Störe meine Kreise nicht!), worauf dieser dermaßen in Rage geriet, dass er Archimedes erschlug.

Nach Plutarch (Marc. 17,12) hatte Archimedes sich testamentarisch ein Grab mit der Darstellung von Kugel und Zylinder gewünscht, da er offensichtlich auf seine Abhandlung „perì sphaíras kaì kylíndrou“ (Über Kugel und Zylinder), besonders stolz war.

Einzelnachweise

1. ↑ Archimedes. In: MacTutor History of Mathematics archive (englisch)
2. ↑ NOVA | Infinite Secrets | TV Program Description | PBS
3. ↑ Archimedes: Über schwimmende Körper und die Sandzahl. in: Ostwalds Klassiker der exakten Wissenschaften. Nr. 213. Leipzig 1925.
4. ↑ Archimedes
5. ↑ Newsoffice 2005: Archimedes

Literatur

Werkausgaben

• Archimedis opera (editio princeps), ed. Th. Gechauff, Basel 1544
• Archimedis opera omnia (3 vol.), ed. J. L. Heiberg, Lipsiae 1881/1915
• Archimède (4 vol.), ed. Ch. Mugler, Paris 1971

Übersetzungen und Sekundärliteratur

• Ivo Schneider: Archimedes. Ingenieur, Naturwissenschaftler und Mathematiker. Wissenschaftliche Buchgesellschaft, Darmstadt 1979. ISBN 3-534-06844-0
• Paul Strathern: Archimedes und der Hebel. Fischer, Frankfurt/M. 2002. ISBN 3-596-14117-6.
• Thuillier, P. – D’Archimède à Einstein (1988), éd. Fayard
• Reviel Netz (Herausgeber und Übersetzer): Works of Archimedes (with a critical edition of the diagrams and a translation of Eutocius commentary), Bd.1, Cambridge University Press 2004 (mit Kommentar, auf drei Bände angelegt), ISBN 0-521-66160-9.
• Reviel Netz, William Noel „Der Codex des Archimedes- das berühmteste Palimpsest der Welt wird entschlüsselt“, C. H. Beck 2007, ISBN 3-406-56336-8 (englisch: The Archimedes Codex, Weidenfeld and Nicholson 2007)
• Thomas Little Heath (Hrsg.): The Works of Archimedes. Cambridge 1897, Dover Publications, Mineola NY 1953, 2002. ISBN 0-486-42084-1.
• Heiberg (Hrsg.): Geometrical Solutions Derived from Mechanics. Open Court Publ., Chicago/La Salle Ill. 1909, 1942.
• István Száva, Heinrich Weissling (Übers.): Der Gigant von Syrakus. Roman. Prisma, Leipzig 1960, Corvina, Budapest 1960, 1968, 1978.
• Plutarch: Marcellus (17, 12)
• Klaus Geus: Mathematik und Biografie: Anmerkungen zu einer Vita des Archimedes. In: Erler, Michael; Schorn, Stefan (Hrsg.): Die griechische Biographie in hellenistischer Zeit: Akten des internationalen Kongresses vom 26.–29. Juli 2006 in Würzburg. Berlin; New York: Walter de Gruyter, 2007. S. 319–33 (Beiträge zur Altertumskunde; 245).

Weblinks

 Commons: Archimedes – Album mit Bildern und/oder Videos und Audiodateien

 Wikiquote: Archimedes – Zitate

Digitalisate:

• Archimdus tu Syrakusiu ta mechri nyn szomena, hapanta. Basileae 1544, Online-Ausgabe der Sächsischen Landesbibliothek – Staats- und Universitätsbibliothek Dresden
• Des Unvergleichlichen Archimedis Sand-Rechnung, Oder Tiefsinnige Erfindung einer, mit verwunderlicher Leichtigkeit aussprechlichen, Zahl. Nürnberg 1667, Online-Ausgabe der Sächsischen Landesbibliothek – Staats- und Universitätsbibliothek Dresden
• Des Unvergleichlichen Archimedis Kunst-Bücher Oder Heutigs Tags befindliche Schrifften. Nürnberg 1670, Online-Ausgabe der Sächsischen Landesbibliothek – Staats- und Universitätsbibliothek Dresden

Von Archimedes

• Archimedes in der „Bibliotheca Augustana“
  • Darunter besonders hervorzuheben ist: Die Messung des Kreises
• Archimedes über die Parabel

Über Archimedes

• Fakten über Archimedes (englisch)
• Archimedes – Das Genie der Antike
• Archimedes’ Leben und Werk

Normdaten: PND: 118503863 (PICA) | LCCN: n80104666 | VIAF: 29547910 | WorldCat | WP-Personeninfo