Raumfüllung

Raumfüllung bezieht sich auf das Ausfüllen von (in der Regel) 3-dimensionalen euklidischen Räumen mit Gebilden, die höchstens dieselbe Dimension besitzen wie dieser Raum. Raumfüllungen können trivialerweise vollständig sein, d. h. das gesamte Volumen wird belegt (wie bei einem vollständig gefüllten Glas), oder teilweise, was zu dem interessanten Problem der räumlich dichtesten Kugelpackung führt. In vielen praktischen Anwendungen ist man daran interessiert, die Dichte der Füllung zu optimieren, zum Beispiel in der Verpackungsindustrie. Raumfüllungen mathematisch abstrahiert findet man u. a. bei den raumfüllenden Kurven, wo fraktale Gebilde mit einer gebrochenzahligen Dimension kleiner der Raumdimension n und größer als n−1 zur Füllung benutzt werden. Natürliche Quasi-Fraktale dieser Art finden sich häufig als Versorgungsnetzwerke in biologischen Organismen (Blutgefäßsystem, Tracheensystem).

Raumfüllung mit Polyedern

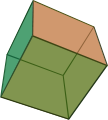
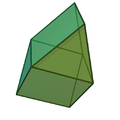
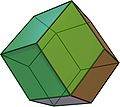
Eine lückenlose Raumfüllung durch Polyeder wird auch als Parkettierung des (dreidimensionalen) Raumes bezeichnet. Versucht man den Raum mit Polyedern einer Art zu füllen, gibt es unter den konvexen Polyedern, die durch regelmäßige Vielecke begrenzt sind, genau fünf, die den Raum alleine füllen: Würfel, dreieckiges und sechseckiges Prisma, Oktaederstumpf und der verdrehte Doppelkeil (Johnson-Körper J₂₆, auch Gyrobifastigium). Unter den sogenannten Catalanischen Körpern ist lediglich der Rhombendodekaeder raumfüllend.

• 

  Würfel

• 

  sechseckiges Prisma

• 

  dreieckiges Prisma

• 

  verdrehter Doppelkeil

• 

  Oktaederstumpf

• 

  Rhombendodekaeder

Siehe auch

• Kristallgitter
• 3D-Parkettierung