Catalanische Körper

Ein catalanischer Körper oder auch dual-archimedischer Körper ist ein Körper, der sich zu einem archimedischen Körper dual verhält. So ist zum Beispiel das Rhombendodekaeder dual zum Kuboktaeder. Benannt sind catalanische Körper nach dem belgischen Mathematiker Eugène Charles Catalan.

Die dual-archimedischen Körper bestehen nur aus einer Flächenart, nämlich identischen nichtregelmäßigen Vielecken, haben aber mindestens zwei verschiedene Arten von Ecken (das Rhombendodekaeder hat zum Beispiel Ecken, an die drei Rhomben, und solche, an die vier Rhomben grenzen). Damit sind sie keine archimedischen Körper im ursprünglichen Sinne mehr. Es gibt 13 catalanische Körper.

Siehe auch: platonischer Körper

Übersicht der catalanischen Körper

Catalanischer Körper	Bild	Dualer Körper	Flächen	Ecken	Kanten	Flächenform	Symmetrie
Triakistetraeder	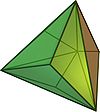(abgestumpftes Tetraeder	12	8	18	gleichschenkliges Dreieck	$T_d\$
Rhombendodekaeder	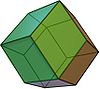(Kuboktaeder	12	14	24	Rhombus	$O_h\$
Triakisoktaeder	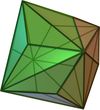(abgestumpftes Hexaeder	24	14	36	gleichschenkliges Dreieck	$O_h\$
Tetrakishexaeder	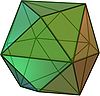(abgestumpftes Oktaeder	24	14	36	gleichschenkliges Dreieck	$O_h\$
Deltoidalikositetraeder	(Rhombenkuboktaeder	24	26	48	Deltoid	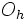$O_h\$
Hexakisoktaeder	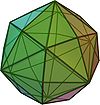(abgestumpftes Kuboktaeder	48	26	72	unregelmäßiges Dreieck	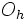$O_h\$
Pentagonikositetraeder	(Animation)	abgeschrägtes Hexaeder	24	38	60	unregelmäßiges Fünfeck	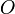$O\$
Rhombentriakontaeder	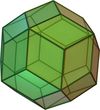(Ikosidodekaeder	30	32	60	Rhombus	$I_h\$
Triakisikosaeder	(abgestumpftes Dodekaeder	60	32	90	gleichschenkliges Dreieck	$I_h\$
Pentakisdodekaeder	(abgestumpftes Ikosaeder	60	32	90	gleichschenkliges Dreieck	$I_h\$
Deltoidalhexakontaeder	(Rhombenikosidodekaeder	60	62	120	Deltoid	$I_h\$
Disdyakistriakontaeder oder Hexakisikosaeder	(abgestumpftes Ikosidodekaeder	120	62	180	unregelmäßiges Dreieck	$I_h\$
Pentagonhexakontaeder	(Animation)	abgeschrägtes Dodekaeder	60	92	150	unregelmäßiges Fünfeck	$I\$