Raumwinkel

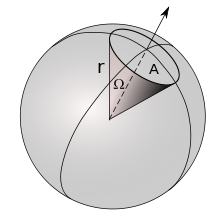
Der Raumwinkel beschreibt die Größe eines Raumbereichs, der von einem Kegelmantel aufgespannt wird.

Kegelmantel in einer Kugel

Definition

Der Raumwinkel Ω einer beliebigen Fläche A entspricht dem Quotienten der Fläche A, die sich ergibt, wenn man A auf eine Kugel vom Radius r projiziert, dividiert durch r²:

$\Omega:=\frac{A}{r^2}=\int\!\!\!\!\int_A \frac{\hat{\vec{n}}\cdot \mathrm{d}\vec{a}}{\rho^2}$

wobei $\hat{\vec{n}}$ der Einheitsvektor vom Ursprung, $\mathrm{d}\vec{a}$ das differentielle Flächenelement und ρ dessen Abstand vom Ursprung ist.

Die Einheit des Raumwinkels

Der Raumwinkel hat die Einheit Steradiant (sr). Ein Raumwinkel von 1 sr umschließt auf einer Kugel mit dem Radius 1 m eine Fläche von 1 m². Da die ganze Kugeloberfläche den Flächeninhalt S = 4πr² besitzt, ist der zugehörige volle Raumwinkel

$\Omega = 4 \pi \approx 12{,}57\ \mathrm{sr}$.

Der Raumwinkel kann auch in Quadratgrad angegeben werden. 1 Quadratgrad entspricht $\left(\tfrac{2\pi}{360}\right)^2$ (rund 0,00030462) Steradiant.

In Anwendungsfeldern wie der Lichttechnik, bei denen intensiv mit Raumwinkeln gerechnet wird, ist es hilfreich, schon an der verwendeten Einheit erkennen zu können, welche physikalische Größe gemeint ist. Lichtstärke zeigt im Gegensatz zum Lichtstrom seine Abhängigkeit vom Raumwinkel durch das Auftreten des Steradiant unter den Einheiten.

Kanonischer Raumwinkel

Wählt man als Umrissform auf der Kugeloberfläche einen Kreis, so erhält man den kanonischen Raumwinkel. Der Raumwinkel bildet dann einen geraden Kreiskegel, in dessen Spitze der Mittelpunkt der Kugel liegt.

Der Öffnungswinkel ω des Kegels lässt sich in den Raumwinkel umrechnen:

$\Omega = 2 \pi \left(1-\cos\frac{\omega}{2}\right) = 4 \pi \sin^2 \frac{\omega}{4}$

Öffnungswinkel ω in rad

2π

π

2/3 π

1/2 π

1/3 π

1/4 π

1/6 π

in °

360°

180°

120°

90°

65,5°

60°

50°

45°

40°

30°

20°

15°

10°

1°

Raumwinkel Ω in sr

12,57

6,28

3,14

1,84

1,000

0,842

0,589

0,478

0,379

0,214

0,0955

0,0538

0,0239

0,000239

Raumwinkel und Kugelkoordinaten

Ein Raumwinkel aus einem kartesischen Polarkoordinatenabschnitt

In einem Kugelkoordinatensystem kann der Raumwinkel besonders übersichtlich definiert werden, da es keine radiale Variable gibt. Zwei Meridianwinkel φ₁, φ₂ und zwei Breitenwinkel γ₁, γ₂ bestimmen ein Flächenelement auf einer Kugeloberfläche. Der zugehörige Raumwinkel beträgt:

$\Omega = \int\limits_{\varphi_1}^{\varphi_2}\int\limits_{\gamma_1}^{\gamma_2} \sin \gamma \, \mathrm{d}\gamma \, \mathrm{d}\varphi$

Oosterom-und-Strackee-Algorithmus

Ein effizienter Algorithmus zur Berechnung des Raumwinkels eines allgemeinen Dreiecks mit Vektoren R₁, R₂ und R₃ – betrachtet vom Ursprung – wurde im Jahr 1983 von Oosterom und Strackee^[1] bewiesen zu:

$\tan \left( \frac{1}{2} \Omega \right) = \frac{ \mathrm{det} \left( \vec{r}_1,\vec{r}_2,\vec{r}_3 \right) } { \| \vec{r}_1 \| \| \vec{r}_2 \| \| \vec{r}_3 \| + \langle \vec{r}_1 , \vec{r}_2 \rangle \| \vec{r}_3 \| + \langle \vec{r}_1 , \vec{r}_3 \rangle \| \vec{r}_2 \| + \langle \vec{r}_2 , \vec{r}_3 \rangle \| \vec{r}_1 \|}$.

Raumwinkel einer Pyramide

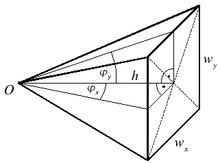
Der Spezialfall des Raumwinkels mit einem rechteckigen und ebenen Umriss entspricht der geometrischen Form einer Pyramide, wobei der Ursprung genau senkrecht über dem Mittelpunkt des ebenen Rechtecks stehe, s. Abbildung. Dieser Raumwinkel tritt z.B. bei der Berechnung des Etendue von optischen Systemen mit rechteckigen Aperturen auf.

Zum Raumwinkel einer Pyramide

Er lässt sich sehr leicht über den Oosterom-und-Strackee-Algorithmus berechnen. Mit der Pyramidengrundfläche w_x und w_y sowie der Höhe h ergibt sich:

$\Omega = 4 \arctan \frac{w_x \cdot w_y}{2h\cdot \sqrt{4 h^2 + w_x^2 + w_y^2}}$

Verwendet man für die Berechnung die beiden Öffnungswinkel 2φ_x und 2φ_y (wobei tan φ_x = w_x/2h und tan φ_y = w_y/2h), so folgt nach einigen trigonometrischen Umformungen:

$\Omega = 4 \arcsin \left( \sin \varphi_x \sin \varphi_y \right)$

Schreibweise

∢

Für den Formelsatz steht das Zeichen »∢« (TeX \sphericalangle, Unicode U+2222 SPHERICAL ANGLE, keine HTML-Entity) zur Verfügung, das sich im Unicode-Block Mathematische Operatoren findet. Das Zeichen entspricht den angloamerikanischen Gewohnheiten, im europäischen Formelsatz ist ein zum Verwechseln ähnliches Zeichen für den ebenen Winkel üblich.

Weblinks

 Commons: Solid angle – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

1. ↑ A. Van Oosterom, J. Strackee: The Solid Angle of a Plane Triangle. In: Biomedical Engineering, IEEE Transactions on. BME-30, Nr. 2, 1983, S. 125–126, doi:10.1109/TBME.1983.325207.