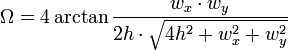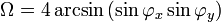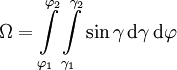- ∢
-
Physikalische Größe Name Raumwinkel Größenart Raumwinkel Formelzeichen der Größe Ω, ω Größen- und
Einheiten-
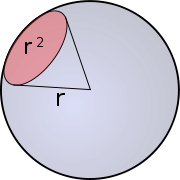
systemEinheit Dimension SI Steradiant (sr) 11) Anmerkungen 1) Verhältnisgröße Der Raumwinkel Ω ist als geometrische Größe des dreidimensionalen Raumes das Pendant zum (für die Ebene definierten) Winkel. Er kann definiert werden als Teilfläche S einer Kugel, dividiert durch das Quadrat des Radius r der Kugel:
- Ω = S / r2
Bei Betrachtung der Einheitskugel (r = 1) entspricht eine Teilfläche also unmittelbar dem zugehörigen Raumwinkel. So ist der volle Raumwinkel gleich der Oberfläche der Einheitskugel, nämlich 4π.
Obwohl der Raumwinkel eine dimensionslose Größe ist, wird er zur Verdeutlichung in der Einheit Steradiant angegeben. Dies entspricht dem Bogenmaß mit der Einheit Radiant beim ebenen Winkel.
Ein Raumwinkel von 1sr umschließt auf einer Kugel mit dem Radius 1m eine Fläche von 1m2.
Definition
Der Raumwinkel Ω einer beliebigen Fläche A entspricht dem Quotienten der Fläche S, die sich ergibt, wenn man A auf eine Kugel vom Radius r projiziert, dividiert durch r2:
wobei
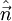 der Einheitsvektor vom Ursprung,
der Einheitsvektor vom Ursprung, 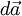 das differentielle Flächenelement und ρ dessen Abstand vom Ursprung ist.
das differentielle Flächenelement und ρ dessen Abstand vom Ursprung ist.Die Einheit des Raumwinkels
Da der Raumwinkel das Verhältnis zweier Flächen ist, hat er im SI (Internationales Einheitensystem) die abgeleitete Einheit 1 m²/m²; ihr ist im SI der besondere Name Steradiant mit dem Einheitenzeichen sr gegeben worden. Da 1 sr = 1 m²/m² = 1 ist, kann das Einheitenzeichen sr grundsätzlich auch weggelassen werden. In Anwendungsfeldern, bei denen intensiv mit Raumwinkeln gerechnet wird, ist es aber hilfreich, schon an der verwendeten Einheit erkennen zu können, welche physikalische Größe gemeint ist. Deswegen lässt man in der Lichttechnik "sr" nie weg. Die SI-Einheiten für Lichtstärke und Lichtstrom unterscheiden sich nur durch Steradiant.
Schreibweise
∢Für den Formelsatz steht das Zeichen »∢« (TeX
\sphericalangle, Unicode U+2222 SPHERICAL ANGLE, keine HTML-Entity) zur Verfügung, das sich im Unicode-Block Mathematische Operatoren findet. Das Zeichen entspricht den angloamerikanischen Gewohnheiten, im europäischen Formelsatz ist ein zum Verwechseln ähnliches Zeichen für den ebenen Winkel üblich.Veranschaulichung
Folgendes Bild veranschaulicht die Situation:
Anders als das Bild vielleicht vermuten ließe, spielt die Umrissform des Flächenstücks keine Rolle. Jede Umrissform auf der Kugeloberfläche mit dem gleichen Flächeninhalt definiert einen Raumwinkel der gleichen Größe. Legt man durch jeden Punkt der Umrissform eine Halbgerade (auch Strahl genannt) mit dem Mittelpunkt der Kugel als Startpunkt, dann erhält man eine geometrische Figur, die den Raumwinkel veranschaulicht. (Dies ist vergleichbar mit der Darstellung für einen Winkel in der Ebene: Zwei Halbgeraden mit einem gemeinsamen Startpunkt.)
Der volle Raumwinkel
Da die ganze Kugeloberfläche den Flächeninhalt S = 4πr2 besitzt, ist der zugehörige volle Raumwinkel
Unabhängigkeit vom Kugelradius
Man betrachte zwei konzentrische Kugeln mit den Radien r1 und r2, und ein Flächenstück S auf der ersten Kugel. Man nehme nun alle Strahlen aus dem Mittelpunkt der Kugeln durch S.
Die Schnittpunkte der Strahlen mit der zweiten Kugel bilden eine Fläche S'. Deren Fläche beträgt dann das
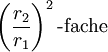 von S, da alle Abmessungen im Verhältnis
von S, da alle Abmessungen im Verhältnis  verändert wurden. Der Raumwinkel bleibt aber unverändert und damit unabhängig vom Kugelradius.
verändert wurden. Der Raumwinkel bleibt aber unverändert und damit unabhängig vom Kugelradius.Kanonischer Raumwinkel
Wählt man als Umrissform einen Kreis, so erhält man den kanonischen Raumwinkel. Der Raumwinkel bildet dann einen geraden Kreiskegel, in dessen Spitze der Mittelpunkt der Kugel liegt.
Bei einem gegebenen Öffnungswinkel ω des Kegels berechnet sich der Raumwinkel zu
Man sieht, dass der Vollwinkel - die Umrissform erfasst dabei alle Raumrichtungen per ω = 2π - dem vollen Raumwinkel von 4π entspricht.
Oosterom-und-Strackee-Algorithmus
Ein effizienter Algorithmus zur Berechnung des Raumwinkels eines allgemeinen Dreiecks mit Vektoren R1, R2 und R3 – betrachtet vom Ursprung – wurde von Oosterom und Strackee[1] bewiesen zu:
wobei:
- [R1R2R3] eine Determinante darstellt,
- Ri ist der Abstand des Punktes i zum Ursprung,
- Ri·Rj ist das Skalarprodukt der beiden Vektoren.
Raumwinkel einer Pyramide
Der Spezialfall des Raumwinkels mit einem rechteckigen und ebenen Umriß entspricht der geometrischen Form einer Pyramide, wobei der Ursprung genau senkrecht über dem Mittelpunkt des ebenen Rechtecks stehe, s. Abbildung. Dieser Raumwinkel tritt z.B. bei der Berechnung des Etendue von optischen Systemen mit rechteckigen Aperturen auf.
Er lässt sich sehr leicht über den Oosterom-und-Strackee-Algorithmus berechnen. Mit der Pyramidengrundfläche wx und wy sowie der Höhe h ergibt sich:
Verwendet man für die Berechnung die beiden Öffnungswinkel 2φx und 2φy (wobei tan φx = wx/2h und tan φy = wy/2h), so folgt nach einigen trigonometrischen Umformungen:
Zusammenhang zwischen Raumwinkel und Kugelkoordinaten
In einem Kugelkoordinatensystem bestimmen der Meridianwinkel φ und der Breitenwinkel γ einen Punkt auf einer Kugeloberfläche, jeweils zwei Winkel φ1, φ2, γ1 und γ2 ein Flächenelement. Der zugehörige Raumwinkel beträgt:
Weblinks
Einzelnachweise
Wikimedia Foundation.

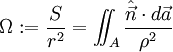

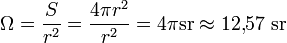

![\tan \left( \frac{1}{2} \Omega \right) =
\frac{[ {\mathbf R}_{1}{\mathbf R}_{2}{\mathbf R}_{3}]}{ R_{1}R_{2}R_{3} + ( {\mathbf R}_{1} \cdot {\mathbf R}_{2})R_{3} + ( {\mathbf R}_{1} \cdot {\mathbf R}_{3})R_{2} + ( {\mathbf R}_{2} \cdot {\mathbf R}_{3})R_{1}}](/pictures/dewiki/49/1943f0d78dbb5fc2c86a441e28b97f95.png)