Reflexionsfaktor

Der Begriff Reflexionsfaktor (auch Reflexionskoeffizent) ist in der Physik das Amplitudenverhältnis zwischen reflektierter und einfallender Welle beim Übergang in ein anderes Ausbreitungsmedium.

Die Amplitude bezieht sich dabei auf die skalare oder vektorielle Feldgröße, beispielsweise die elektrische Spannung auf einer Leitung, den Druck beim Schall oder die elektrische Feldstärke bei elektromagnetischen Wellen. Der Reflexionsfaktor ist negativ, wenn bei der Reflexion die Feldgröße ihr Vorzeichen umkehrt. Für transversale Wellen hängt der Reflexionsfaktor von der Polarisation ab, siehe Fresnelsche Gleichungen.

Der Reflexionsfaktor wird unter anderem verwendet, um den Reflexionsgrad zu berechnen, der sich auf die Leistung oder Intensität der Welle bezieht, siehe Energiegröße. Dieser wird oft für ein ganzes Bauteil statt für einen einzelnen Übergang angegeben und kann durch Interferenz stark von der Wellenlänge abhängen, siehe Fabry-Perot-Interferometer.

Reflexion in Leitungen

Bei der Ausbreitung von elektromagnetischen Wellen auf Leitungen entsteht am Leitungsende eine Reflexion, wenn die dort angeschlossene Schaltung eine vom Wert der Wellenimpedanz Z_l abweichende Eingangsimpedanz Z_a besitzt. Das Verhältnis von reflektierter zu hinlaufender Spannungswelle wird als Reflexionsfaktor bezeichnet und wird nach folgender Gleichung berechnet ^[1]:

$r = \frac{U_\mathrm{r}}{U_h} = \frac{Z_\mathrm{a} - Z_\mathrm{l}}{Z_\mathrm{a} + Z_\mathrm{l}} \qquad |r| \le 1$

Dabei bedeuten

• Z_l: der Wellenwiderstand der Leitung,
• Z_a: der Eingangswiderstand der am Leitungsende angeschlossenen Schaltung.
• U_h: die Spannung der hinlaufenden Welle
• U_r: die Spannung der rücklaufenden Welle

Für Z_a = Z_l wird der Reflexionsfaktor zu Null. Dieser Zustand wird angestrebt, weil dann die maximale Leistung übertragen wird. Man spricht dann von Impedanzanpassung oder Leistungsanpassung. Das ist bei komplexen, zusammengeschalteten Baugruppen und Geräten in der Praxis nicht komplett zu erreichen. Da zudem üblicherweise ein Frequenzband übertragen wird, ist die Impedanzanpassung bei frequenzabhängigen Widerständen nur für eine Frequenz (typischerweise die Träger- oder Mittenfrequenz) mit Hilfe von Resonanztransformatoren möglich.

Rückflussdämpfung

Insbesondere bei der Beschreibung von Leitungseigenschaften wird häufig der Begriff der Rückflussdämpfung R verwendet. Der Rückflussdämpfungsfaktor bezeichnet das Verhältnis von gesendeter Leistung zu reflektierter Leistung. Da die Leistung proportional zum Betragsquadrat der Spannung ist, kann der Rückflussdämpfungsfaktor durch den Reflexionsfaktor ausgedrückt werden:

$R = \frac{P_\mathrm{h}}{P_\mathrm{r}} = \left|\frac{U_\mathrm{h}}{U_\mathrm{r}}\right|^2 = \frac{1}{\left|r\right|^2} \,$

Wenn man den Rückflussdämpfungsfaktor logarithmiert, erhält man das Rückflussdämpfungsmaß, das üblicherweise in der Pseudoeinheit Dezibel (dB) angegeben wird:

$\begin{align} a &= 10\,\mathrm{dB} \cdot \lg R \\ &= -20\,\mathrm{dB} \cdot \lg \left|r\right| \\ &= -20\,\mathrm{dB} \cdot \lg \left| \frac{Z_\mathrm{a} - Z_\mathrm{l}}{Z_\mathrm{a} + Z_\mathrm{l}} \right| \end{align}$

Leitungstheorie

In der Leitungstheorie ist der Reflexionskoeffizient Γ definiert als:

$\Gamma=\frac{E_1^-}{E_1^+}=\frac{Z_\mathrm{w2}-Z_\mathrm{w1}}{Z_\mathrm{w2}+Z_\mathrm{w1}}$

Er tritt überall dort auf, wo eine Welle auf eine Grenzfläche zwischen zwei Medien (1 und 2) mit unterschiedlichen Materialeigenschaften stößt. Dabei ist $E_1^-$ der Phasor der reflektierten Welle und $E_1^+$ die einlaufende Welle des Mediums 1. Z_wi ist dabei gerade die Wellenimpedanz des Mediums i. Der Reflexionskoeffizient ist dimensionslos.

Hingegen ist der Transmissionskoeffizient T definiert als:

$T=\frac{E_2^+}{E_1^+}=\frac{2 Z_\mathrm{w2}}{Z_\mathrm{w2}+Z_\mathrm{w1}}$

T kann auch aus Γ wie folgt gewonnen werden: T = 1 + Γ

Wasserwellen

Reflexionskoeffizient C(f)

Reflexionskoeffizient C(x)

Bei monochromatischen Wasserwellen ist der Reflexionskoeffizient als Quotient aus der Höhe der reflektierten Welle H_r und der Höhe der anlaufenden Welle H_i definiert.

C_r = H_r / H_i < 1

Er kann versuchstechnisch aus den resultierenden Wasserspiegelauslenkungen der an einem Bauwerk partiell stehenden Welle ermittelt werden.

$C_\mathrm{r} = \frac{H_\mathrm{r}}{H_\mathrm{i}} = \frac{H_{\max}-H_{\min}}{H_{\max}+H_{\min}}$

Darin bedeuten:

• H_max  = H_i + H_r
• H_min  = H_i − H_r.

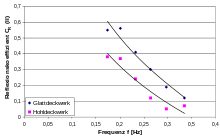
Für die Analyse der frequenzabhängigen Reflexion von Wellenspektren seeseitig eines Bauwerkes können für definierte Frequenzbänder i an Stelle der überlagerten vertikalen Wasserspiegelauslenkungen auch die Extremwerte der integrierten Energiedichte E_max ,i und E_min ,i verwendet werden.

$C_{\mathrm{r},i} = \frac{\sqrt{E_{\max, i}}-\sqrt{E_{\min ,i} }}{\sqrt{E_{\max ,i}} + \sqrt{E_{\min, i}}}$

mit

• E_max,i = Betrag des Energiemaximums der zur Partialwelle beitragenden Frequenzkomponenten am Schwingungsbauch und
• E_min,i = Betrag des Energieminimums der zur Partialwelle beitragenden Frequenzkomponenten am Schwingungsknoten.

Siehe auch

• Smith-Diagramm
• Streuparameter

Weblinks

• Akustische Wellen und Felder - Abschnitt 5.1.15 - DEGA-Empfehlung 101 (PDF-Datei; 1016 kB)

Einzelnachweise

1. ↑ Klaus Ruppert: Interaktives Lehrbeispiel in JAVA zum Verhalten elektrischer Leitungen. Diplomica Verlag, Hamburg 1998 (Diplomarbeit, Fachhochschule Gießen-Friedberg, 1998, Kapitel 10.5 Der Reflexionsfaktor)