Leitungstheorie

Die Leitungstheorie ist ein Teilgebiet der Elektrotechnik. Sie befasst sich sowohl in der Hochfrequenztechnik, als auch in der elektrischen Energieversorgung mit Erscheinungen auf Leitungen, deren Länge in der Größenordnung der Wellenlänge des übertragenen Signalspektrums oder darüber liegt. Sie beschäftigt sich mit der mathematischen Beschreibung von Leitungen für Elektromagnetische Wellen mithilfe der aus der maxwellschen Theorie abgeleiteten Leitungsgleichungen, die ein Differentialgleichungssystem bilden.

Hintergrund

Allgemein lässt sich eine Leitung nur grob mit dem ohmschen Widerstand aus Leitungsquerschnittsfläche, Leitfähigkeit und Länge beschreiben. Sobald die Wellenlänge in der Größenordnung der Leitungslänge liegt oder z. B. Schaltvorgänge auf Leitungen beschrieben werden sollen, reicht dieses stark vereinfachte Modell nicht hin.

Mithilfe der Leitungsgleichungen und den zugehörigen Größen wie Wellenimpedanz, Reflexionsfaktor, Leitungsbelägen und weiteren Parametern, lassen sich Ausgleichsvorgänge auf Leitungen und Wellenerscheinungen berechnen.

Beaufschlagt man eine Leitung mit einem Wechselstrom oder mit einem Strom- oder Spannungspuls, so wird das Signalausbreitungsverhalten auf der Leitung durch ohmsche, kapazitive und induktive Leitungseigenschaften (die sog. Leitungsbeläge) bestimmt.

Sinnvoll wird eine leitungstheoretische Betrachtung in der Regel, wenn die geometrischen Abmessungen der Leitungen die gleiche Größenordnung haben oder länger sind, als die Wellenlänge der Strom- oder Spannungsgröße. Eine Wechselspannung von 1 GHz besitzt im Vakuum eine Wellenlänge von rund 30 cm. Wellenvorgänge spielen auf den Platinen moderner Computer eine große Rolle. Somit wären moderne Computer mit hochfrequenter Taktung ohne Anwendung der Leitungstheorie undenkbar.

Die Leitungsgleichungen

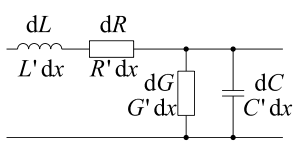
Die Leitungsgleichungen lassen sich aus dem Ersatzschaltbild eines infinitesimal kurzen Leitungsabschnitts bestimmen. Die folgende Abbildung zeigt das Ersatzschaltbild eines Leitungsabschnitts der infinitesimalen Länge dx:

vereinfachtes Ersatzschaltbild einer Zweidrahtleitung

Die darin enthaltenen Größen sind auf die Länge dx bezogene Beläge: Der Induktivitätsbelag L′, der Kapazitätsbelag C′, der Widerstandsbelag R′ und der Ableitungsbelag G′. Aus der Spannung U und dem Strom I an der Leitung ergeben sich die beiden Differentialgleichungen der homogenen Leitung:

$\frac{\mathrm{d}U}{\mathrm{d}x} = -(R' + j\omega L') I$

$\frac{\mathrm{d}I}{\mathrm{d}x} = -(G' + j\omega C') U$

Aus diesen Leitungsgleichungen lässt sich u. a. die Wellenimpedanz bestimmen.

Leitungstransformation

Transformation im Smith-Diagramm

Als Leitungstransformation bezeichnet man in der Leitungstheorie den Effekt, der einen Widerstand am Ende einer von einem Hochfrequenzgenerator gespeisten Leitung am Anfang der Leitung als komplexe Impedanz, in Spezialfällen also auch als Kondensator oder Spule, erscheinen lässt.

Leitungstransformationen lassen sich relativ einfach mithilfe eines Smith-Diagrammes durchführen: Man dreht dazu den normierten Abschlusswiderstand z im Smith-Diagramm lediglich im Winkel

$\phi = -\frac{360^\circ}{0{,}5} \cdot \frac{L}{\lambda} = -\frac{360^\circ}{0{,}5} \cdot \frac{L f \sqrt{\epsilon_r}}{c_0}$

um den Punkt z = 1 (Leitungslänge L, Generatorfrequenz f, relative Dielektrizitätszahl $\epsilon_r$, Vakuum-Lichtgeschwindigkeit c₀). Die normierte Eingangsimpedanz lässt sich dann direkt aus dem Smith-Diagramm ablesen.

Des Weiteren lässt sich die am Eingang der Transformationsleitung wirkende Impedanz Z₁ auch mathematisch berechnen. In nachfolgender Formel ergibt sich die Impedanz Z₁ aus der Trafoleitung Z_Ltg und L_Ltg sowie der am Ausgang angeschlossenen Impedanz Z₂.

$Z_1 = Z_\mathrm{Ltg} {{Z_2+j Z_\mathrm{Ltg} \tan 2 \pi {L_{Ltg} \over \lambda}} \over {Z_\mathrm{Ltg}+j Z_2 \tan 2 \pi {L_\mathrm{Ltg} \over \lambda}}}$

wobei für $2 \pi {L_\mathrm{Ltg} \over \lambda} = \beta L_\mathrm{Ltg}= b$ weitere häufig verwendete Notationen sind.

Sonderfall Kurzschluss

Für eine am Ende kurzgeschlossene Leitung (Z₂ = 0) vereinfacht sich die Gleichung zu

$Z_1 = Z_\mathrm{Ltg} \cdot j \tan 2 \pi \frac{L_\mathrm{Ltg}}{\lambda}$

Das Verhältnis L_Ltg/λ = m bestimmt auf Grund der Vorzeichenregeln der Tangensfunktion, ob sich diese U-förmige Leitung wie eine Kapazität, eine Induktivität oder ein Schwingkreis verhält:

• Für 1/4 > m > 0 ist es eine Induktivität
• Für 1/4 = m ist es ein Parallelschwingkreis mit den Resonanzwellenlängen λ; λ/3; λ/5; …
• Für 1/2 > m > 1/4 ist es eine Kapazität.
• Für 1/2 = m ist es ein Reihenschwingkreis mit den Resonanzwellenlängen λ; λ/2; λ/4; …
• Für 3/4 > m > 1/2 ist es eine Induktivität
• …

Anmerkung: In allen Gleichungen ist als L_Ltg die elektrische Leitungslänge einzusetzen. Diese errechnet sich aus der geometrischen Länge nach der Formel

$L_\mathrm{Ltg} = \frac{L_\mathrm{geometrisch}}{VKF}$

wobei VKF der Verkürzungsfaktor des Kabels ist.

In Funkgeräten für sehr hohe Frequenzen wird bei Stichleitungen bzw. Lecher-Leitungen ein verschiebbarer Kurzschlussbügel verwendet, um die gewünschte Eigenschaft einstellen zu können. Im Regelfall wird keine symmetrische Doppelleitung verwendet, die Energie abstrahlt und deshalb nur einen geringen Gütefaktor besitzt, sondern ein geschlossener, zylindersymmetrischer Topfkreis.

Für Mikrostreifenleitungen auf Leiterplatten gibt es erweiterte Formeln (siehe Streifenleitung#Leitungswellenwiderstand).

Sonderfall Leerlauf

Für eine am Ende offene Leitung (Z₂ → ∞) vereinfacht sich die Gleichung zu

$Z_1=\frac {Z_\mathrm{Ltg}}{j \tan 2 \pi \frac{L_\mathrm{Ltg}}{\lambda}}=-jZ_\mathrm{Ltg}\cot 2 \pi \frac{L_\mathrm{Ltg}}{\lambda}$

Das Verhältnis L_Ltg/λ = m bestimmt, ob sich diese U-förmige Leitung wie eine Kapazität, eine Induktivität oder ein Schwingkreis verhält:

• Für 1/4 > m > 0 ist es eine Kapazität
• Für 1/4 = m ist es ein Reihenschwingkreis mit den Resonanzwellenlängen λ; λ/2; λ/4; …
• Für 1/2 > m > 1/4 ist es eine Induktivität.
• Für 1/2 = m ist es ein Parallelschwingkreis mit den Resonanzwellenlängen λ; λ/3; λ/5; …
• Für 3/4 > m > 1/2 ist es eine Kapazität
• …

Sonderfall λ/4

Eine λ/4-lange Leitung mit der Wellenimpedanz Z_k transformiert zwischen Ein- und Ausgang gemäß der Formel

$Z_\mathrm{e} = \frac{Z_\mathrm{k}^2}{Z_\mathrm{a}}$

Energieeinspeisung in einen Hohlleiter; im rechten Bild Ansicht von oben

Wird eine λ/4-lange Leitung (Koax- oder Bandleitung) am Ende kurzgeschlossen (Z_e = 0), wirkt diese am Eingang wie ein Leerlauf (also hochohmig, Z_a → ∞). Umgekehrt wirkt eine am Ende offene λ/4-lange Leitung am Eingang wie ein Kurzschluss. Das Z_k spielt in beiden Fällen keine Rolle.

Manche Bauelemente der Radartechnik wie Branch-Duplexer basieren auf der Impedanztransformation von λ/4-Leitungen.

In einen Hohlleiter wird die elektrische Energie mit einer Sonde (Stabantenne) eingekoppelt, die λ/4 vom geschlossenen Ende entfernt in den Hohlleiter hineinragt. Die sich von der Sonde des Kopplers ablösende elektromagnetische Welle „sieht” an drei Seiten den unendlich hohen Widerstand der kurzgeschlossenen λ/4- Leitung, kann sich also nur in der verbleibenden Richtung ausbreiten.

Sonderfall λ/2

Eine λ/2-lange Leitung mit der Wellenimpedanz Z_k transformiert zwischen Ein- und Ausgang nicht; Man kann also eigentlich nicht von einer „Transformation“ reden.

Z_e = Z_a

Wird eine λ/2-lange Leitung (Koax- oder Bandleitung) am Ende kurzgeschlossen (Z_e = 0), wirkt sie auch am Eingang wie ein Kurzschluss. Umgekehrt wirkt eine am Ende offene λ/2-lange Leitung auch am Eingang wie ein Leerlauf. Das Z_k spielt in beiden Fällen keine Rolle.

Siehe auch

• Koaxialkabel
• Abschlusswiderstand
• Anpassung
• Reflexion
• Stichleitung
• Elektrische Länge