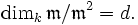Regulärer lokaler Ring — Im mathematischen Teilgebiet der kommutativen Algebra versteht man unter einem regulären lokalen Ring einen noetherschen lokalen Ring, dessen maximales Ideal von d Elementen erzeugt werden kann, wenn d die Dimension des Ringes bezeichnet.… … Deutsch Wikipedia
Ring Magdeburger Fußball-Vereine — Der Ring Magdeburger Fußball Vereine (RMFV) war ein lokaler Fußballverband in der Stadt Magdeburg. Der Verband wurde im Jahre 1897 gegründet. Sieben Vereine spielten eine Mischung aus Fußball mit und ohne Aufnehmen des Balles, also aus… … Deutsch Wikipedia
Gaußscher Ring — Ein faktorieller Ring (auch ZPE Ring oder Gaußscher Ring) ist eine algebraische Struktur, und zwar ein Integritätsring, in dem jedes Element eine eindeutige Zerlegung in irreduzible Faktoren besitzt (Achtung: ein faktorieller Ring ist etwas… … Deutsch Wikipedia
ZPE-Ring — Ein faktorieller Ring (auch ZPE Ring oder Gaußscher Ring) ist eine algebraische Struktur, und zwar ein Integritätsring, in dem jedes Element eine eindeutige Zerlegung in irreduzible Faktoren besitzt (Achtung: ein faktorieller Ring ist etwas… … Deutsch Wikipedia
Elementarteilersatz — In der Algebra bezeichnet man Integritätsbereiche als Hauptidealringe oder Hauptidealbereiche, wenn jedes Ideal ein Hauptideal ist. Die wichtigsten Beispiele für Hauptidealringe sind der Ring der ganzen Zahlen sowie Polynomringe in einer… … Deutsch Wikipedia
Hauptidealbereich — In der Algebra bezeichnet man Integritätsbereiche als Hauptidealringe oder Hauptidealbereiche, wenn jedes Ideal ein Hauptideal ist. Die wichtigsten Beispiele für Hauptidealringe sind der Ring der ganzen Zahlen sowie Polynomringe in einer… … Deutsch Wikipedia
Hurwitzquaternion — Eine Hurwitzquaternion (oder Hurwitz Ganzzahl) in der Mathematik ist eine Quaternion, deren vier Koeffizienten entweder alle (rational )ganzzahlig oder alle halbzahlig (Hälften ungerader ganzer Zahlen) sind – Mischungen von Ganzzahlen und… … Deutsch Wikipedia
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Fehlstand — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
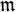 und Restklassenkörper k. Dann heißt A regulär, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist:
und Restklassenkörper k. Dann heißt A regulär, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist: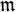 kann von d Elementen erzeugt werden.
kann von d Elementen erzeugt werden.